外接球是幾何學中的基本概念，三維空間中一個多面體的外接球是一個使得該多面體的所有頂點都在其上的球面，這時稱這個多面體為球內接多面體，外接球的球心被稱為該多面體的外心。[1]
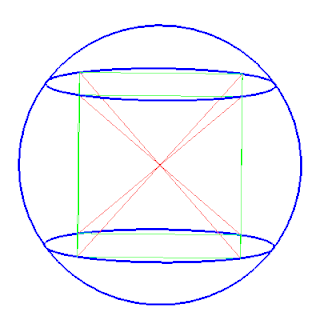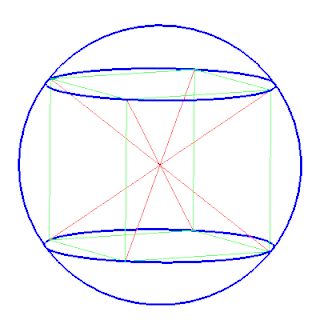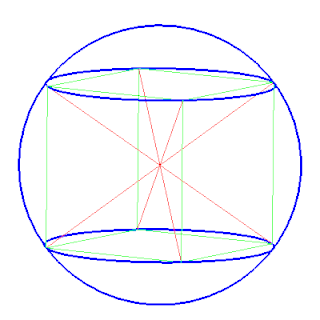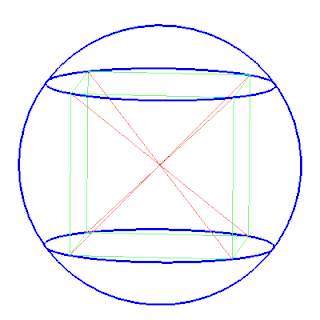
每個多面體至多有一個外接球。也就是說，如果某個多面體有外接球，那麼它的外接球是唯一的。並非所有的多面體都有外接球。四面體以及正多面體、正多角錐、正多稜柱都有外接球。
四面體的外接球
可以證明，每個四面體都有外接球。外接球的球心在四面體任一條邊的垂直平分面上，它在四面體每一面上的投影，都是那個面的三角形的外心。
參見
參考來源
外部連結
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
