Θ函數

數學中，Θ函數是一種多複變（英語：Several complex variables）特殊函數。其應用包括阿貝爾簇（英語：Abelian variety）與模空間、二次形式、孤立子理論；其格拉斯曼代數推廣亦出現於量子場論，尤其於超弦與D-膜理論。

Jacobi theta 1

Jacobi theta 2

Jacobi theta 3

Jacobi theta 4

Θ函數最常見於橢圓函數理論。相對於其「z」 變量，Θ函數是擬周期函數（quasiperiodic function），具有「擬周期性」。在一般下降理論（英語：Descent (mathematics)）中，Θ函數是來自線叢條件。

雅可比Θ函數

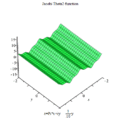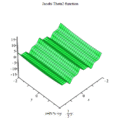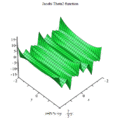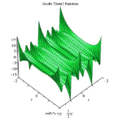
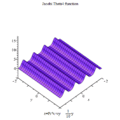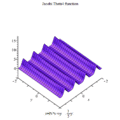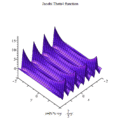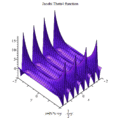
雅可比Θ函數取二變量${\displaystyle z\,}$與${\displaystyle \tau \,}$，其中${\displaystyle z\,}$為任何複數，而${\displaystyle \tau \,}$為上半複平面上一點；此函數之定義為：

${\displaystyle \vartheta (z;\tau )=\sum _{n=-\infty }^{\infty }\ e^{(\pi in^{2}\tau +2\pi inz)}}$。

若固定${\displaystyle \tau \,}$ ，則此成為一週期為${\displaystyle 1\,}$的單變量${\displaystyle (z)\,}$整函數的傅里葉級數：

${\displaystyle \vartheta (z+1;\tau )=\vartheta (z;\tau )}$ 。

在以 ${\displaystyle \tau \,}$ 位移時，此函數符合：

${\displaystyle \vartheta (z+a+b\tau ;\tau )=\ e^{(-\pi ib^{2}\tau -2\pi ibz)}\vartheta (z;\tau )}$；

其中 ${\displaystyle a\,}$與${\displaystyle b\,}$為整數。

• 
• 
• 
• 

輔助函數

可定義輔助函數：

${\displaystyle \vartheta _{01}(z;\tau )=\vartheta (z+{\frac {1}{2}};\tau )}$

${\displaystyle \vartheta _{10}(z;\tau )=e^{{\frac {\pi {\mathrm {i} }\tau }{4}}+\pi {\mathrm {i} }z}\vartheta (z+{\frac {\tau }{2}};\tau )}$

${\displaystyle \vartheta _{11}(z;\tau )=e^{{\frac {\pi {\mathrm {i} }\tau }{4}}+\pi {\mathrm {i} }(z+{\frac {1}{2}})}\vartheta (z+{\frac {\tau +1}{2}};\tau ).}$

其中符號依黎曼與芒福德之習慣；雅可比的原文用變量${\displaystyle q=e^{\pi {\mathrm {i} }\tau }\,}$替換了${\displaystyle \tau \,}$，而稱本條目中的Θ為${\displaystyle \theta _{3}\,}$，${\displaystyle \vartheta _{01}}$為${\displaystyle \theta _{0}\,}$，${\displaystyle \vartheta _{10}}$為${\displaystyle \theta _{2}\,}$，${\displaystyle \vartheta _{11}}$為${\displaystyle -\theta _{1}\,}$。

若設${\displaystyle z=0\,}$，則我們可從以上獲得四支單以${\displaystyle \tau \,}$為變量之函數，其中${\displaystyle \tau \,}$取值於上半複平面。此等函數人稱「Θ『常量』」（theta constant）；我們可以用Θ函數定義一系列模形式，或參數化某些曲線。由「雅可比 恆等式」可得：

${\displaystyle \vartheta (0;\tau )^{4}=\vartheta _{01}(0;\tau )^{4}+\vartheta _{10}(0;\tau )^{4}}$,

是為四次費馬曲線。

雅可比恆等式

雅可比恆等式描述模羣在Θ函數之作用；模羣之生成元為T: τ ↦ τ+1與S: τ ↦ -1/τ。我們已有 T 作用之式。設：

${\displaystyle \alpha =(-{\mathrm {i} }\tau )^{\frac {1}{2}}e^{{\pi {\mathrm {i} }z^{2}}{\tau }}\,}$

則

${\displaystyle \vartheta ({\frac {z}{\tau }};-{\frac {1}{\tau }})=\alpha \vartheta (z;\tau )}$

${\displaystyle \vartheta _{01}({\frac {z}{\tau }};-{\frac {1}{\tau }})=\alpha \vartheta _{10}(z;\tau )}$

${\displaystyle \vartheta _{10}({\frac {z}{\tau }};-{\frac {1}{\tau }})=\alpha \vartheta _{01}(z;\tau )}$

${\displaystyle \vartheta _{11}({\frac {z}{\tau }};-{\frac {1}{\tau }})=-\alpha \vartheta _{11}(z;\tau )}$

以nome q表示Θ函數

我們可用變量${\displaystyle w\,}$與${\displaystyle q\,}$，代替${\displaystyle z\,}$與${\displaystyle \tau \,}$，來表示ϑ。設${\displaystyle w=e^{\pi {\mathrm {i} }z}\,}$而${\displaystyle q=e^{\pi {\mathrm {i} }\tau }\,}$。則ϑ可表示為：

${\displaystyle \vartheta (w;q)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}$

而輔助Θ函數可表示為：

${\displaystyle \vartheta _{01}(w;q)=\sum _{n=-\infty }^{\infty }(-1)^{n}w^{2n}q^{n^{2}},}$

${\displaystyle \vartheta _{10}(w;q)=q^{\frac {1}{4}}\sum _{n=-\infty }^{\infty }w^{2n+1}q^{n^{2}+n},}$

${\displaystyle \vartheta _{11}(w;q)={\mathrm {i} }q^{\frac {1}{4}}\sum _{n=-\infty }^{\infty }(-1)^{n}w^{2n+1}q^{n^{2}+n}.}$

此表示式不需要指數函數，所以適用於指數函數無每一處定義域，如p進數域。

乘積表示式

雅可比三重積恆等式（Jacobi's triple product identity）中指出：若有複數${\displaystyle w\,}$和${\displaystyle q\,}$，其中${\displaystyle |q|<1\,}$而${\displaystyle w\neq 0\,}$，則

${\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+w^{2}q^{2m-1}\right)\left(1+w^{-2}q^{2m-1}\right)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}$

此式可以用基本方法證明，如戈弗雷·哈羅德·哈代和愛德華·梅特蘭·賴特共同編著的《數論導引》（英語：An Introduction to the Theory of Numbers）。

若用nome變量${\displaystyle q=e^{\pi i\tau }\,}$與${\displaystyle w=e^{\pi iz}\,}$表示，則有：

${\displaystyle \vartheta (z;\tau )=\sum _{n=-\infty }^{\infty }\exp(\pi i\tau n^{2})\exp(\pi iz2n)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}$

由此得到Θ函數的積公式：

${\displaystyle \vartheta (z;\tau )=\prod _{m=1}^{\infty }\left(1-\exp(2m\pi i\tau )\right)\left(1+\exp((2m-1)\pi i\tau +2\pi iz)\right)\left(1+\exp((2m-1)\pi i\tau -2\pi iz)\right)}$

三重積等式左邊可以擴展成：

${\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+(w^{2}+w^{-2})q^{2m-1}+q^{4m-2}\right),}$

即

${\displaystyle \vartheta (z|q)=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right)}$。

這個式子在z取實值時尤為重要。 各輔助Θ函數亦有類似之積公式：

${\displaystyle \vartheta _{01}(z|q)=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right).}$

${\displaystyle \vartheta _{10}(z|q)=2q^{1/4}\cos(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m}+q^{4m}\right).}$

${\displaystyle \vartheta _{11}(z|q)=-2q^{1/4}\sin(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m}+q^{4m}\right).}$

積分表示式

雅可比Θ函數可用積分表示，如下：

${\displaystyle \vartheta (z;\tau )=-i\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}\cos(2uz+\pi u) \over \sin(\pi u)}du}$

${\displaystyle \vartheta _{01}(z;\tau )=-i\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}\cos(2uz) \over \sin(\pi u)}du.}$

${\displaystyle \vartheta _{10}(z;\tau )=-ie^{iz+i\pi \tau /4}\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}\cos(2uz+\pi u+\pi \tau u) \over \sin(\pi u)}du}$

${\displaystyle \vartheta _{11}(z;\tau )=e^{iz+i\pi \tau /4}\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}\cos(2uz+\pi \tau u) \over \sin(\pi u)}du}$

與黎曼ζ函數的關係

黎曼常用關係式

${\displaystyle \vartheta (0;-{\frac {1}{\tau }})=(-i\tau )^{\frac {1}{2}}\vartheta (0;\tau )}$

以證黎曼ζ函數之函數方程。他寫下等式：

${\displaystyle \Gamma \left({\frac {s}{2}}\right)\pi ^{-{\frac {s}{2}}}\zeta (s)={\frac {1}{2}}\int _{0}^{\infty }\left[\vartheta (0;it)-1\right]t^{\frac {s}{2}}{\frac {dt}{t}}}$ ；

而此積分於替換${\displaystyle s\to 1-s}$下不變。 ${\displaystyle z\,}$非零時之積分，在赫爾維茨ζ函數一文有描述。

與基本橢圓函數之關係

雅可比用Θ函數來構造橢圓函數，並使其有易於計算之形式，因為Θ函數中快速收斂的級數往往比積分容易計算。他表示他的橢圓函數成兩枚上述Θ函數之商，這可參見雅可比橢圓函數的定義。魏爾施特拉斯橢圓函數亦可由雅可比Θ構造：

${\displaystyle \wp (z;\tau )=-(\log \vartheta _{11}(z;\tau ))''+c}$

其中二次微分相對於z，而常數c使${\displaystyle \wp (z)}$的羅朗級數（於 z = 0）常項為零，因為雅可比橢圓函數單位胞腔內兩極點互為相反數，和為零，而魏爾施特拉斯橢圓函數的所有極點留數均為零，所以這是必要的。

與模形式之關係

設η為戴德金η函數。則

${\displaystyle \vartheta (0;\tau )={\frac {\eta ^{2}\left(\tau +{\frac {1}{2}}\right)}{\eta (2\tau +1)}}}$.

解熱方程

雅可比Θ函數為一維熱方程、於時間為零時符合週期邊界條件之唯一解。 設z = x取實值，τ = it而t取正值。則有

${\displaystyle \vartheta (x,it)=1+2\sum _{n=1}^{\infty }\exp(-\pi n^{2}t)\cos(2\pi nx)}$

此解此下方程：

${\displaystyle {\frac {\partial }{\partial t}}\vartheta (x,it)={\frac {1}{4\pi }}{\frac {\partial ^{2}}{\partial x^{2}}}\vartheta (x,it)}$。

於t = 0時，Θ函數成為「狄拉克梳狀函數」（Dirac comb）

${\displaystyle \lim _{t\rightarrow 0}\vartheta (x,it)=\sum _{n=-\infty }^{\infty }\delta (x-n)}$，

其中δ為狄拉克δ函數，故可知此解是唯一的。 因此，一般解可得自t = 0時的（週期）邊界條件與Θ函數的卷積。

與海森堡羣之關係

雅可比Θ函在海森堡羣之一離散子羣作用下不變。見海森堡羣之Θ表示一文。

推廣

若F為一n元二次型，則有一關連的Θ函數

${\displaystyle \theta _{F}(z)=\sum _{m\in Z^{n}}\exp(2\pi izF(m))}$

其中Zⁿ為整數格。此Θ函數是模羣（或某適當子羣）上的權n/2 模形式。在其富理埃級數

${\displaystyle \theta _{F}(z)=\sum _{k=0}^{\infty }R_{F}(k)\exp(2\pi ikz)}$

中，R_F(k) 稱為此模形式之「表示數」（representation numbers）。

拉馬努金Θ函數

主條目：拉馬努金Θ函數

黎曼Θ函數

設

${\displaystyle \mathbb {H} _{n}=\{F\in M(n,\mathbb {C} )\;\mathrm {s.t.} \,F=F^{T}\;{\textrm {and}}\;{\mbox{Im}}F>0\}}$

為一集對稱方矩陣，其虛部為正定，一般稱H_n為「西格爾上半平面」（Siegel upper half-plane），它是上半複平面的高維推廣。模羣之n維推廣為辛羣Sp(2n,Z)： 當n = 1 時， Sp(2,Z) = SL(2,Z)。同餘子群（congruence subgroup）的n維推廣為態射核${\displaystyle {\textrm {Ker}}\{{\textrm {Sp}}(2n,\mathbb {Z} )\rightarrow {\textrm {Sp}}(2n,\mathbb {Z} /k\mathbb {Z} )\}}$。

若設${\displaystyle \tau \in \mathbb {H} _{n}}$，則可定義黎曼Θ函數：

${\displaystyle \theta (z,\tau )=\sum _{m\in Z^{n}}\exp \left(2\pi i\left({\frac {1}{2}}m^{T}\tau m+m^{T}z\right)\right)}$；

${\displaystyle \theta (z,\tau )=\sum _{m\in Z^{n}}\exp \left(2\pi i\left({\frac {1}{2}}m^{T}\tau m+m^{T}z\right)\right)}$；

其中${\displaystyle z\in \mathbb {C} ^{n}}$為一n維複向量，上標T為轉置。然則雅可比Θ函數為其特例（設n = 1、 ${\displaystyle \tau \in \mathbb {H} }$；其中${\displaystyle \mathbb {H} }$為上半平面）。

在${\displaystyle \mathbb {C} ^{n}\times \mathbb {H} _{n}.}$的緊緻子集上，黎曼Θ函數絶對一致收歛。

函數方程為：

${\displaystyle \theta (z+a+\tau b,\tau )=\exp 2\pi i\left(-b^{T}z-{\frac {1}{2}}b^{T}\tau b\right)\theta (z,\tau )}$；

此方程成立於 ${\displaystyle a,b\in \mathbb {Z} ^{n}}$, ${\displaystyle z\in \mathbb {C} ^{n}}$ ， ${\displaystyle \tau \in \mathbb {H} _{n}}$。

q-Θ函數

主條目：q-Θ函數

參考文獻

• Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4. (See section 16.27ff.)
• Naum Illyich Akhiezer, Elements of the Theory of Elliptic Functions, (1970) Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 (1990) AMS, Rhode Island ISBN 0-8218-4532-2
• Hershel M. Farkas and Irwin Kra, Riemann Surfaces (1980), Springer-Verlag, New York. ISBN 0-387-90465-4 (See Chapter 6 for treatment of the Riemann theta)
• G. H. Hardy and E. M. Wright，An Introduction to the Theory of Numbers, fourth edition (1959) , Oxford University Press
• David Mumford，Tata Lectures on Theta I (1983), Birkhauser, Boston ISBN 3-7643-3109-7
• James Pierpont Functions of a Complex Variable, Dover
• Harry E. Rauch and Hershel M. Farkas, Theta Functions with Applications to Riemann Surfaces, (1974) Williams & Wilkins Co. Baltimore ISBN 0-683-07196-3.

本條目含有來自PlanetMath《Integral representations of Jacobi theta functions》的內容，版權遵守創用CC協議：署名-相同方式共享協議。