循环群

在群论中，循环群（英文：cyclic group），是指能由单个元素所生成的群。有限循环群同构于整数同余加法群 ${\displaystyle \mathbb {Z} {\big /}n\mathbb {Z} }$，无限循环群则同构于整数加法群。每个循环群都是阿贝尔群，亦即其运算是可交换的。在群论中，循环群的性质已经被研究的较为透彻，是更为复杂的代数研究中常用到的基础工具。

群论
群
基本概念 子群 · 正规子群 · 商群 · 群同态 · 像 · (半)直积 · 直和 单群 · 有限群 · 无限群 · 拓扑群 · 群概形 · 循环群 · 幂零群 · 可解群 · 圈积 离散群 有限单群分类 循环群 Zn 交错群 An 李型群 散在群 马蒂厄群 M11..12,M22..24 康威群 Co1..3 扬科群 J1..4 费歇尔群（英语：Fischer group）F22..24 子魔群（英语：sub monster group） B 魔群 M 其他有限群 对称群, Sn 二面体群, Dn 无限群 整数, Z 模群, PSL(2,Z) 和 SL(2,Z) 连续群 李群 一般线性群 GL(n) 特殊线性群 SL(n) 正交群 O(n) 特殊正交群 SO(n) 酉群 U(n) 特殊酉群 SU(n) 辛群 Sp(n) G2 F4 E6 E7 E8 劳仑兹群 庞加莱群 无限维群 共形群 微分同胚群 环路群 量子群 O(∞) SU(∞) Sp(∞) 代数群 椭圆曲线 线性代数群（英语：Linear algebraic group） 阿贝尔簇（英语：Abelian variety）
查 论 编

定义

6次单位根在乘法下形成循环群。z是本原元而 z² 不是，因为z的奇数次幂不是z²的幂。

设 ${\displaystyle (G,\cdot )}$ 为一个群，若存在一个元素 ${\displaystyle g\in G}$，使得 ${\displaystyle G=\left\langle \,g\,\right\rangle =\left\{g^{k}|\;k\in \mathbb {Z} \right\}}$，则 ${\displaystyle (G,\cdot )}$ 形成一个循环群。群 ${\displaystyle G}$ 内任意一个元素所生成的群都是循环群，而且是 ${\displaystyle G}$ 的子群。

分类

令循环群 ${\displaystyle G=\left\{g^{k}|\;k\in \mathbb {Z} \right\}}$。如果存在两个相异整数 ${\displaystyle m,n}$ 使得 ${\displaystyle g^{m}=g^{n}}$，那么 ${\displaystyle d=\vert m-n\vert }$ 满足 ${\displaystyle g^{d}=e}$，其中 ${\displaystyle e}$ 是单位元。所以对于任意整数 ${\displaystyle k}$，${\displaystyle g^{k}=g^{r}}$，其中 ${\displaystyle r}$ 是 ${\displaystyle k}$ 除以 ${\displaystyle d}$ 得到的余数，${\displaystyle 0\leq r\leq d-1}$。这说明 ${\displaystyle G}$ 是有限群。设 ${\displaystyle d_{m}}$ 是所有这样的正整数中最小的一个，则 ${\displaystyle G}$ 可以表示为：

${\displaystyle G=\left\{g^{k}|\;k=0,1,\ldots ,d_{m}-1\right\}}$

可以证明它同构于模 ${\displaystyle d_{m}}$ 的加法群 ${\displaystyle \left(\mathbb {Z} {\big /}d_{m}\mathbb {Z} ,+\right)}$。事实上，对每一个正整数 ${\displaystyle n}$，都存在唯一一个（在同构的意义上）阶为此正整数 ${\displaystyle n}$ 的循环群。而所有的 ${\displaystyle n}$ 阶循环群都和模 ${\displaystyle n}$ 的同余类构成的加法群 ${\displaystyle \left(\mathbb {Z} {\big /}n\mathbb {Z} ,+\right)}$ 同构。如果一个循环群的阶是无限的，那么它同构于整数关于加法构成的群 ${\displaystyle \left(\mathbb {Z} ,+\right)}$。因此，循环群已被完全分类，是最简单的一种群。

例如，${\displaystyle G=\left\{e,g,g^{2},g^{3},g^{4},g^{5}\right\}}$，则 ${\displaystyle G}$ 为循环群。${\displaystyle G}$ 同构于模 ${\displaystyle 6}$ 的加法群：${\displaystyle \mathbb {Z} _{6}=\left\{{\overline {0}},{\overline {1}},{\overline {2}},{\overline {3}},{\overline {4}},{\overline {5}}\right\}}$。考虑映射：

${\displaystyle \varphi :\;G\longrightarrow \mathbb {Z} _{6}}$

${\displaystyle \left.\;\,\right.g^{k}\,\mapsto \;\,{\overline {k}}}$

可以证明其为群同态，而且是双射，因此是群同构。

标记

由于循环群必然是阿贝尔群，且与加法群 ${\displaystyle \mathbb {Z} {\big /}n\mathbb {Z} }$ 或整数的加法群 ${\displaystyle \mathbb {Z} }$ 同构，它的运算常以加法表示并记为 ${\displaystyle \mathbb {Z} _{n}}$。然而数论中一般会避免使用这种标记，因为它和p进整数构成的环或群的局部化的标记相冲突，容易混淆。因此，数论中一般直接记作 ${\displaystyle \mathbb {Z} {\big /}n\mathbb {Z} }$，或以乘法表示运算并记为 ${\displaystyle C_{n}}$。

性质

每一个循环群要么同构于整数模 ${\displaystyle n}$ 的加法群：${\displaystyle \mathbb {Z} _{n}=\left\{{\overline {0}},{\overline {1}},{\overline {2}},\cdots ,{\overline {n-1}}\right\}}$，要么同构于整数的加法群 ${\displaystyle \mathbb {Z} }$。因此要研究循环群的性质，只需要研究 ${\displaystyle \mathbb {Z} _{n}}$和 ${\displaystyle \mathbb {Z} }$ 作为加法群的性质即可。设 ${\displaystyle G}$ 是一个 ${\displaystyle n}$ 阶的循环群^{[N 1]}，${\displaystyle g\in G}$，则：

• ${\displaystyle G}$ 为交换群。这是因为 ${\displaystyle g+h\equiv h+g{\pmod {n}}}$ 。
• 若 ${\displaystyle n}$ 为正整数，则 ${\displaystyle g^{n}=e}$，因为${\displaystyle n\equiv 0{\pmod {n}}}$ 。而且 ${\displaystyle n}$ 是所有使得 ${\displaystyle g^{k}=e}$ 的正整数 ${\displaystyle k}$ 中最小的一个。
• 若 ${\displaystyle n}$ 为无限大，则 ${\displaystyle G}$ 有且仅有两个生成元，分别对应于整数中的 ${\displaystyle 1}$ 和 ${\displaystyle -1}$。
• 若 ${\displaystyle n}$ 为正整数，则 ${\displaystyle G}$ 的各个生成元分别对应整数模 ${\displaystyle n}$ 加法群中与 ${\displaystyle n}$ 互质的数的同余类。例如当 ${\displaystyle n=12}$ 时，${\displaystyle G}$ 的生成元有四个，分别对应着 ${\displaystyle \mathbb {Z} _{12}}$ 中的${\displaystyle {\overline {1}},{\overline {5}},{\overline {7}},{\overline {11}}}$四个同余类。
• ${\displaystyle G}$ 的每一个子群都是循环群。每一个 ${\displaystyle G}$ 的 ${\displaystyle m}$ 阶有限子群皆为整数模 ${\displaystyle m}$ 的加法群。而每一个 ${\displaystyle G}$ 的无限子群都可以表示成 ${\displaystyle m\mathbb {Z} }$，同构于 ${\displaystyle \mathbb {Z} }$。
• 设 ${\displaystyle p}$ 是素数，则阶为 ${\displaystyle p}$ 的群都同构于 ${\displaystyle p}$ 阶循环群。
• 两个循环群的直积 ${\displaystyle \mathbb {Z} _{n}\times \mathbb {Z} _{m}}$是循环群当且仅当 ${\displaystyle n}$ 和 ${\displaystyle m}$ 互素。故 ${\displaystyle \mathbb {Z} _{12}}$ 同构于 ${\displaystyle \mathbb {Z} _{3}\times \mathbb {Z} _{4}}$，而不是 ${\displaystyle \mathbb {Z} _{2}\times \mathbb {Z} _{6}}$^{[N 2]}。
• 阿贝尔群的基本定理说明每一个有限生成阿贝尔群都是有限多个循环群的直积。

例子

在二维和三维空间里，${\displaystyle n}$ 折旋转对称的对称群为 ${\displaystyle C_{n}}$，属 ${\displaystyle \mathbb {Z} _{n}}$ 抽象群类型。在三维里，亦存在其他代数地相同的对称群，详见三维点群。

需留意的是，圆的所有旋转所组成之群S¹(圆群)不是循环的，甚至不是可数的。

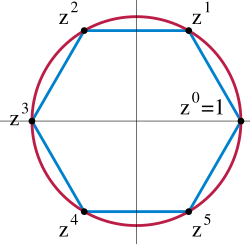
• ${\displaystyle n}$ 次单位根形成一个关于乘法的 ${\displaystyle n}$ 阶循环群。

• 每一个有限域之有限扩张的伽罗瓦群是有限且循环的；相反地，给定一有限域F和一有限循环群 ${\displaystyle G}$，则存在一个 ${\displaystyle F}$ 的有限域扩张，其伽罗瓦群为 ${\displaystyle G}$。

表示

有限循环群的环图全是有着其元素在各个角上的 ${\displaystyle n}$ 边形。下面环图中的黑角表示是单位元，而其他的角则为群的其他元素。一个环包括著连接着单位元之元素的接续之次方。

Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8

子群

所有循环群的子群及商群都是循环群。特别地，${\displaystyle \mathbb {Z} }$ 的子群为 ${\displaystyle m\mathbb {Z} }$ 的形式，其中 ${\displaystyle m}$ 为非负整数。对于不同的 ${\displaystyle m}$ ，形如 ${\displaystyle m\mathbb {Z} }$ 的子群都不同，且除了平凡群（${\displaystyle m=0}$）外都同构于 ${\displaystyle \mathbb {Z} }$ 。 ${\displaystyle \mathbb {Z} }$ 的子群格同构于以可除性排序之自然数格的对偶。除了一个平凡的反例 ${\displaystyle \mathbb {Z} \backslash \{0\}}$ 外， ${\displaystyle \mathbb {Z} }$ 的所有商群都是有限的。对每个 ${\displaystyle n}$ 的正约数 ${\displaystyle d}$ ，群 ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$ 恰有一个元素数目为 ${\displaystyle d}$ 的子群，它由 ${\displaystyle n/d}$ 的剩余类所产生。其不存在其他的子群。故其子群格会同构于以可除性排序之 ${\displaystyle n}$ 的约数所组成的集合。

特别地，一个循环群是单群当且仅当其元素数目为素数。

举一个实际的问题，给定一个 ${\displaystyle n}$ 目之有限子群 ${\displaystyle C}$，其生成元为 ${\displaystyle g}$，并要求求得以某一整数 ${\displaystyle k}$ 之 ${\displaystyle g^{k}}$ 所生成的子群之大小 ${\displaystyle m}$。这里，${\displaystyle m}$ 会是能使 ${\displaystyle mk}$ 能被 ${\displaystyle n}$ 整除之最小正整数。因此其为 ${\displaystyle n/t}$，其中 ${\displaystyle t}$ 为 ${\displaystyle k}$ 和 ${\displaystyle n}$ 的最大公约数。换句话说，由 ${\displaystyle g^{k}}$ 产生之子群之指标为 ${\displaystyle t}$。其理由在数论中被称为指标计算算法。

自同态

阿贝尔群 ${\displaystyle \mathbb {Z} _{n}}$ 的自同态环会同构于此阿贝尔群，且使其构成一个环。在此同构之下，数字 ${\displaystyle r}$ 会对应于将每个元素映射至其 ${\displaystyle n}$ 次乘积之值上之 ${\displaystyle \mathbb {Z} _{n}}$ 的自同态。此一自同态只有在r和n互素时会是个双射函数，所以 ${\displaystyle \mathbb {Z} _{n}}$ 的自同构群会同构于群 ${\displaystyle \mathbb {Z} _{n}^{\times }}$(见上面)。${\displaystyle \mathbb {Z} _{n}}$ 的自同构群有时会被称为 ${\displaystyle \mathbb {Z} _{n}}$ 的特征群，且此一群的建构会直接导致对狄利克雷特征的定义。

相似地，加法群 ${\displaystyle \mathbb {Z} }$ 的自同态环会同构于环 ${\displaystyle \mathbb {Z} }$ ，且其自同构群会同构于环 ${\displaystyle \mathbb {Z} }$ 的单位群，即${\displaystyle \{-1,+1\}\cong \mathbb {Z} _{2}}$。

逼肖循环群

一个群称为逼肖循环（virtually cyclic）的，如果这个群包含一个有限指数的循环子群。换言之，一个逼肖循环群的任何元素，都可表示为这个循环子群的一个元素乘以群中某个有限子集的一个元素。一个无限群是逼肖循环的，当且仅当这个群是有限生成并且正好有两个端。^[1]逼肖循环群的一个简单例子是 ${\displaystyle \mathbb {Z} /n}$ 和 ${\displaystyle \mathbb {Z} }$ 的直积，因子 ${\displaystyle \mathbb {Z} }$ 有有限指数 ${\displaystyle n}$。任何格罗莫夫双曲群的阿贝尔子群都是逼肖循环群。^[2]

注释

1. n也可以是无限大，约定“n为无穷大”代表群同构于整数加法群。
2. ${\displaystyle \mathbb {Z} _{2}}$和${\displaystyle \mathbb {Z} _{6}}$的直积并不是一个循环群。

参考来源

1. Stallings, John, Groups of cohomological dimension one, Applications of Categorical Algebra (Proc. Sympos. Pure Math., Vol. XVIII, New York, 1968), Providence, R.I.: Amer. Math. Soc.: 124–128, 1970, MR 0255689. 特别见p. 126: "If G has two ends, the explicit structure of G is well known: G is an extension of a finite group by either the infinite cyclic group or the infinite dihedral group."
2. Alonso, J. M.; Brady, T.; Cooper, D.; Ferlini, V.; Lustig, M.; Mihalik, M.; Shapiro, M.; Short, H., Notes on word hyperbolic groups, Group theory from a geometrical viewpoint (Trieste, 1990) (PDF), River Edge, NJ: World Scientific, Corollary 3.6, 1991 [2014-04-01], MR 1170363, （原始内容 (PDF)存档于2013-04-25）

相关文献

• Gallian, Joseph, Contemporary abstract algebra 4th, Boston: Houghton Mifflin, 1998, ISBN 978-0-669-86179-2 （英语）, especially chapter 4.
• Herstein, I. N., Abstract algebra 3rd, Prentice Hall, 1996, ISBN 978-0-13-374562-7, MR1375019, especially pages 53–60.

另见

• 三维循环对称群
• 循环扩张
• 循环模
• 同余