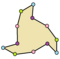
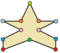
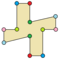
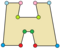
在几何学中,十二边形是指有十二条边和十二个顶点的多边形[1],其内角和为1800度[2]。十二边形有很多种,其中对称性最高的是正十二边形。其他的十二边形依照其类角的性质可以分成凸十二边形和非凸十二边形,其中凸十二边形代表所有内角角度皆小于180度。非凸十二边形可以在近一步分成凹十二边形和星形十二边形,其中星形十二边形表示边自我相交的十二边形。而一般的十字形为凹十二边形常见的一个例子。
正十二边形
正十二边形是指所有边等长、所有角等角的十二边形,由十二条相同长度的边和十二个相同大小的角构成,是一种正多边形。正十二边形的内角是弧度,换算成角度是150度。在施莱夫利符号中用 来表示。由于正十二边形可看作是截去所有顶点的正六边形,即截角的正六边形,因此施莱夫利符号中也可以计为 。而因为正六边形亦可以将正三角形透过截角变换来构造,即切去正三角形的三个顶点,因此正十二边形可以视为正三角形经过2次的截角变换的结果,在施莱夫利符号中亦可以写为 。
若已知正十二边形的边长a,则正十二边形的面积为:
三国时代数学家刘徽计算出半径为的圆形,其内接正12边形的面积为[4][5]。正十二边形面积等于最长对角线平方的四分之三。
十二边形的宽度是两个平行边之间的距离,正好会等于两倍的边心距。因此已知正十二边形的宽度和边长也可以求出面积:
也可以利用三角关系进行验证:
若已知边心距r,正十二边形的周长为:
该系数是已知边心距求面积公式中系数的两倍[7]。
尺规作图可先在圆形内制作正六边形,再将各边二等分线延伸至圆周以完成正十二边形的顶点。
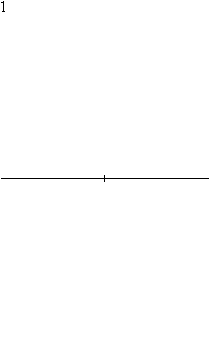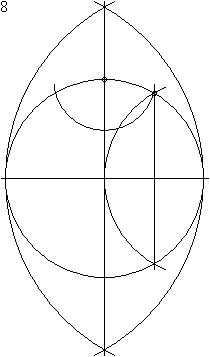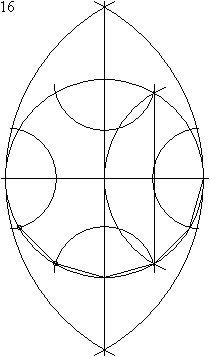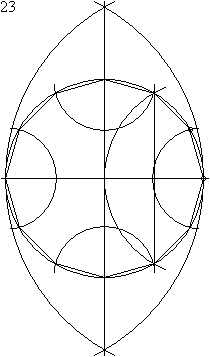
 正六边形、正方形和正三角形 |
 图型块 |
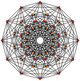
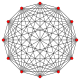
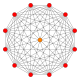
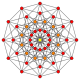
 六维超立方体投影图中的15个菱形 |
 15个菱形 |
有一些正多边形镶嵌图含有正十二边形:
 截角六边形镶嵌3.12.12[9][10] |
 大斜方截半六边形镶嵌: 4.6.12 |
 六角化大斜方截半六边形镶嵌: 3.3.4.12 & 3.3.3.3.3.3 |
对称性

正十二边形具有Dih12对称性,阶数为24.
有15个不同的子群二面体群和环状对称。每个子组对称性允许一个或多个自由不规则形式。只有G12子群没有自由度,但可以看作是有向边。
扭歪十二边形

扭歪十二边形,又称不共面十二边形,是指顶点并非完全共面的十二边形。
扭歪十二边形经常出现在高维多胞体正交投影的皮特里多边形。例如十一维正十二胞体的皮特里多边形就是一个扭歪十二边形,其具有A11 [310] 的考克斯特群的对称性[12]。
使用
参见
参考文献
外部链接
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.