大地水準面

大地水準面（德語：Geoid）是指地球重力場^{[註 1]}中，與處於自由靜止狀態的平均海水面相重合^[3]:49或最為接近^[4]:42的重力等位面。這一概念最早由德國大地測量學家卡爾·弗里德里希·高斯在1828年提出。當時，高斯以「地球的數學表面」^[3]:73來指稱與重力方向相垂直、且與靜止的平均海水面相重合的幾何表面^[5]:4，並提出將其作為高程系統的基準面^[6]:74。其後，高斯的學生利斯廷於1873年創造出了「Geoid」一詞，用以描述高斯所提出的數學表面。^[7]

EGM96（英語：EGM96）^[1]模型給出的全球大地水準面高分佈圖，紅、藍兩色分別表示高於和低於橢球面

在大地測量學中，大地水準面被視作是地球的物理形狀和數學形狀。^[4]:2由於自然的地形表面形態過於複雜，大地測量學通常是將重力場中整體形狀與地形表面最為接近的等位面作為地球的形狀進行研究。^[8]:226處於靜力平衡狀態下的平均海水面被視作是符合這一標準的重力等位面，這一假想的海水面不受潮汐、風浪及大氣壓的變化影響，僅在地球引力和因地球自轉產生的離心慣性力的作用下保持平衡。^[9][4]:41將該平均海水面所處的重力等位面延伸到陸地內部，形成的閉合曲面即為大地水準面，其所包圍的形體又被稱為大地體。^[10]:29

1849年，英國物理學家斯托克斯提出了計算大地水準面的斯托克斯方法，使大地水準面的形狀能夠通過其整個表面上的重力觀測值確定。^[10]:8但在傳統的大地測量中，通過大範圍的重力觀測，以及對這些重力觀測值進行積分而求得大地水準面的方式遇到了諸多困難。^[8]:294-295隨着20世紀中後期衛星重力測量等技術逐漸發展成熟，採用球諧級數表達的地球重力場模型逐漸成為了描述大地水準面的主要方式^[11]，全球尺度下的大地水準面也得以以分米級的精度測定^[12]。莫洛堅斯基、布耶哈馬等大地測量學家，亦在斯托克斯方法的基礎上提出了通過地面測量技術確定大地水準面的新方法。^[5]:34

大地水準面是測量外業所依據的基準面，在測量學中具有重要地位。^[13]在各類高程系統中，日常中稱為海拔高程的正高系統是基於大地水準面建立的。^[10]:42如何確定大地水準面的形狀，是物理大地測量學研究的關鍵問題之一。^[14][15][16]

定義

經典定義

1873年，利斯廷提出了大地水準面的經典定義，即大地水準面是與平均海水面相重合的重力等位面。^[7]在1975年，美國大地測量學家理查德·拉普（英語：Richard H. Rapp）進一步完善了這一定義，他將重力位 ${\displaystyle W}$ 視為除大氣層外的地球質量所引起的重力位 ${\displaystyle W_{g}}$、大氣質量所引起的重力位 ${\displaystyle W_{a}}$，以及受日、月的引潮力作用而引起的重力位 ${\displaystyle W_{t}}$的和：^[17]

${\displaystyle W=W_{g}+W_{a}+W_{t}}$

不同於 ${\displaystyle W_{g}}$，後兩項與地球內部的質量分佈無關，因此可以被相對精確地計算。拉普認為，定義大地水準面的重力位應當僅包含 ${\displaystyle W_{g}}$和 ${\displaystyle W_{a}}$，即大地水準面應當是使 ${\displaystyle W_{g}+W_{a}}$ 等於常數的重力等位面，而因引潮力、風和洋流等其他因素影響產生的變化則不在考慮範圍之內。這種定義方式認為，通過多年的驗潮數據可以得到一個平均海水面，其上的任意一點的位置與海洋面的長期平均位置相重合。^[18]

然而，20世紀60年代以來對平均海水面的研究發現，其與大地水準面間存在最大可達2米的系統性的偏移^[19]，這就使大地水準面的經典定義暴露出了缺陷。因此，馬瑟（英語：Mather R. S.）等人在1978年提出，大地水準面應重新定義為與平均海水面最為密合的重力等位面。^[20]

相對論定義

1985年，瑞典大地測量學家布耶哈馬基於相對論重力提出了相對論大地水準面的概念，即一個使其上所有精密時鐘的運行速率相同且與平均海水面最為密合的封閉曲面。^[21]在2019年，德國不來梅大學的丹尼斯·菲利普（德語：Dennis Philipp）利用新的測量結果，以及無含時紅移勢能（英語：time-independent redshift potential）等新的理論，對相對論大地水準面的概念給出了數學上的表述方法。這一方法給出的相對論水準面與經典大地水準面之間存在着毫米級的差異。^[22]

形狀

表現大地水準面差距的假彩色圖像，差距放大了10,000倍，地形添加了陰影效果

表現大地水準面差距的假彩色圖像，差距按比例表示

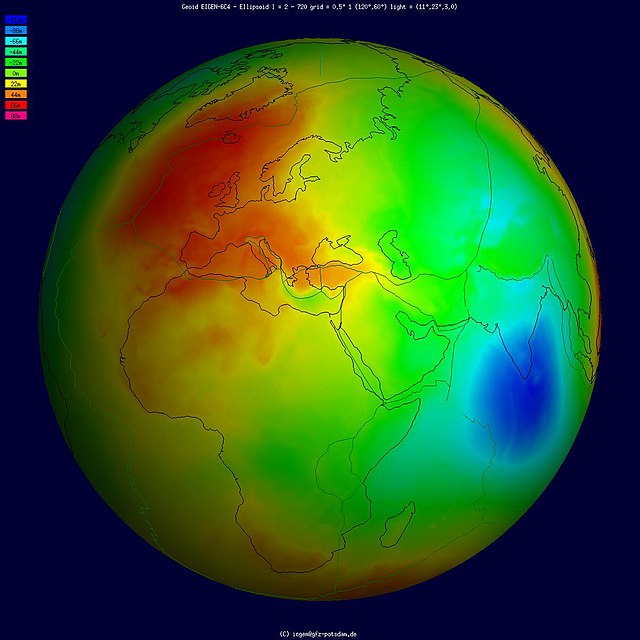
從數學上看，大地水準面是一個連續但不規則的閉合曲面，它與經過這一曲面的鉛垂線處處正交。^[23]:49地球內部的質量分佈，特別是外層的質量分佈的不均勻性，使得大地水準面的形狀變得特別複雜。^[10]:29在發生密度突變的區域，大地水準面的曲率會表現出不連續性。因此，大地水準面並非是解析曲面。^[4]:41

大地水準面的形狀可以用橢球面近似，該橢球面也被稱為參考橢球面。以WGS84坐標系使用的橢球為例，其長半軸位於赤道面上，長度約6,378,137米；短半軸指向極點，長度約6,356,752米，比長半軸短約21千米。^[24]相對於WGS84橢球，大地水準面的起伏從最高點到最低點的範圍僅不到200米。在這一差距被放大的情況下，大地水準面的形狀則與馬鈴薯或梨相似。^[25]儘管大地水準面是一個不規則的曲面，但它仍比真實的地形表面更加平滑，後者的高程差跨越了近20千米。

從赤道觀察大地水準面（紅線）相對於參考橢球面（黑線）的形狀，兩者間的差值為同一緯線上大地水準面差距的平均值

從地極處觀察大地水準面（紅線）相對於參考橢球面（黑線）的形狀，兩者間的差值為同一經線上大地水準面差距的平均值

起伏

主條目：大地水準面高

大地水準面起伏又稱大地水準面高或大地水準面差距，是指大地水準面上的某一點，與其沿法線投影到參考橢球面上的相應位置之間的距離。^[23]:83大地水準面高的正極值出現在新幾內亞，為+85.4米；負極值出現在印度南部，為−107.0米。^[26]

大地水準面起伏的幅度和空間分佈受地球內部密度分佈的直接影響。在頻譜分析中，大地水準面起伏的分佈可分為長波（尺度為上千公里，幅度為±100米左右）、中波（尺度為上百公里，幅度為±10米）和短波（尺度為數十公里，幅度為±1米）部分。^[26]其中，長波部分反映地幔及地球內部的密度異常分佈^[27]，而中短波部分則反映岩石圈和地形的影響。在地球物理學研究中，大地水準面的起伏又可分為地形的不規則部分、結晶基底起伏、莫霍面起伏、岩石圈底面起伏，以及因地幔和地核部分的橫向密度不均勻造成的起伏等。^[28]

EGM96地球重力場模型給出的全球大地水準面高分佈圖

正異常

大地水準面高在北大西洋、歐洲、非洲的西部和南部、印度洋西南部、安地斯山脈、西太平洋及赤道太平洋部分等地表現出正值^[29][30]，世界上所有的大型地盾、顯生宙地台和地質熱點幾乎也都位於這些地區^[31]。其中，分佈較廣而幅度較高的有兩個區域，橫跨了大西洋和非洲的正異常區域被稱為大西洋-非洲大地水準面高值區（英語：Atlantic-African geoid high），太平洋中西部的正異常區域則被稱為赤道太平洋大地水準面高值區（英語：Equatorial Pacific geoid high）。西太平洋的正異常區域在中生代早期曾是俯衝雜岩帶所處的位置。其他與俯衝帶不相關的正異常區域則可能曾是大陸板塊的聚集處，或是古板塊的中心等會發生地幔絕熱現象的地區。地幔的絕熱會使得其本身的溫度升高，其產生的抬升和岩漿作用能夠產生大地水準面的正異常。^[31]

負異常

大地水準面高在印度及印度洋北部，以及南極洲附近表現出負值。其中又以印度洋北部的區域表現得尤其顯著，該區域也被稱為印度洋大地水準面低值區（英語：Indian Ocean geoid low）。^[32]對於這些負異常形成的原因，存在有眾多推測，如軟流層中的淺層物質流^[32]、板塊俯衝在中地幔引起的地幔對流^[33]，以及地幔和地核的邊界處發生的凹陷^[34]等。同時，這些推測也都同意，印度洋大地水準面低值區出現的部分原因是特提斯洋在中生代的俯衝帶來的密度異常。^[35]

測定

利用衛星測高技術確定海水面高度的原理示意圖

測定大地水準面進行的技術手段有多種，包括在地面、船舶和飛機中直接進行重力測量，或是通過天文方法和衛星導航系統進行水準測量以獲取垂線偏差或大地水準面高，又或是利用雷達和人造衛星進行衛星測高來描繪地形表面的高度，以及通過對衛星軌道攝動情況的分析、衛星跟蹤衛星以及衛星重力梯度測量等衛星重力探測技術直接反演地球重力場的中長波分量等。^{[36][37][38][6]:318-319}其所依據的原理是對地面的重力測量數據進行積分（如斯托克斯方法），或將地球重力場以球諧級數的形式表達（如拉普拉斯方法）。^[39]

在人造衛星出現前，斯托克斯方法是測定大地水準面的主要原理，但這種方式在應用過程中存在諸多困難：斯托克斯公式中的積分難以收斂、全球性的觀測數據難以獲得等。^[11]1957年斯普特尼克衛星的升空，揭示了通過人造衛星反演地球重力場的可能性。^[40]從此，使用拉普拉斯方法構建全球的重力場模型，成為了大尺度上表達大地水準面的主要方式。^[11]21世紀後，諸如CHAMP、GOCE和GRACE等新一代重力測量衛星的出現，得以使對地球重力場的研究以空前的精度和空間解像度進行，還使得對地球重力場的時變監測成為可能。^[41][42]

斯托克斯方法

喬治·斯托克斯在1849年提出的斯托克斯定理指出：^[43]在大地水準面的外部沒有質量分佈的情況下，其形狀和其外部的重力場可以由地球的質量、自轉角速度以及大地水準面上的重力觀測值唯一確定，而與其內部的質量分佈無關。^[23]:17這一定理說明，大地水準面的形狀可以通過地面上的重力觀測數據確定。而利用斯托克斯方法確定大地水準面的形狀，需要確定大地水準面高相對於參考橢球面的高程差（即大地水準面高）以及這一高程差在參考橢球面上的位置。^[8]:284這分別可以用斯托克斯公式和維寧·曼尼茲公式進行計算。

值得注意的是，實際上的重力觀測數據是在地形表面，而非大地水準面上得到的。因此，在得到地表的觀測數據後，還需要除去大地水準面外的質量對重力觀測值的影響，並將地面上重力觀測值的位置改正到大地水準面上，這一部分的內容又被稱為重力歸算。^[8]:264通過斯托克斯方法，可以求得較高精度的高程異常並隨之確定相應的大地水準面高，常用於局部重力場模型的建立。^[23]:329

斯托克斯公式

斯托克斯公式給出了大地水準面高與全球大地水準面上的重力異常及其分佈的數學關係：^[43]

${\displaystyle N={R \over 4\pi {\bar {\gamma }}}\iint \limits _{\sigma }\Delta g\,S(\psi )\operatorname {d} \!\sigma }$

上式中，${\displaystyle N}$ 是大地水準面高，${\displaystyle R}$ 是地球的平均半徑^[23]:87，${\displaystyle {\bar {\gamma }}}$ 是全球正常重力的平均值。而對於積分部分，${\displaystyle {\begin{smallmatrix}\iint \limits _{\sigma }\end{smallmatrix}}}$表示在整個單位球面上的積分，${\displaystyle \operatorname {d} \!\sigma }$ 是立體角元素。^[23]:89 ${\displaystyle \Delta g}$ 是單位角元素上的重力異常，由重力測量數據給出的重力位減去計算得到的正常重力位後得到。${\displaystyle S(\psi )}$ 則為斯托克斯函數^[44]，該項是單位球面上的被計算點與重力異常觀測值所在的角元素之間的夾角 ${\displaystyle \psi }$ 的函數。^[23]:94

維寧·曼尼茲公式

在由斯托克斯公式求得大地水準面相對於參考橢球面的高程差後，還需通過垂線偏差改正，將大地水準面上的天文坐標轉換成參考橢球面上的地理坐標。這項改正能夠通過通過維寧·曼尼茲公式計算：^[23]:114

${\displaystyle {\begin{Bmatrix}\xi \\\eta \end{Bmatrix}}={1 \over 4\pi {\bar {\gamma }}}\iint \limits _{\sigma }\Delta g\,{\begin{Bmatrix}\cos {\alpha }\\\sin {\alpha }\end{Bmatrix}}\,S(\psi )\operatorname {d} \!\sigma }$

上式中的 ${\displaystyle \xi }$ 表示天文坐標相對於地理坐標的緯度差， ${\displaystyle \eta }$ 表示天文坐標相對於地理坐標的經度差，${\displaystyle \alpha }$ 則是天文坐標相對於地理坐標的方位角。

拉普拉斯方法

利用引力位在質體外部滿足拉普拉斯方程的特性^[23]:5，可以將其展開成球諧級數進行逼近，球諧級數中的各項係數由地球的各項物理性質確定。這些物理性質，如地球的扁率和重力的不規則性等，會對人造衛星在空間中的運動造成影響，即衛星軌道的攝動。因此通過對衛星軌道進行動力學分析，可以反演出地球的重力場模型。^[45]:149又由於人造衛星對重力場模型中的高階項並不敏感^[6]:319，人造衛星主要用於獲得重力場模型中的低階項，而高階項還需結合地面的重力觀測數據等其他方式獲得。^[16]

拉普拉斯方程的球諧級數解

通過求解球面坐標中的拉普拉斯方程 ${\displaystyle \Delta V=0}$ ，單位球外部（${\displaystyle r>1}$）的引力位可以展開為：^[23]:59

${\displaystyle V={\sum _{n=0}^{\infty }}{\sum _{m=0}^{n}}\left[A_{nm}{R_{nm}(\theta ,\lambda ) \over r^{n+1}}+B_{nm}{S_{nm}(\theta ,\lambda ) \over r^{n+1}}\right]}$

上式中各個量的含義如下：

• ${\displaystyle (r,\theta ,\lambda )}$是空間中某特定點的球坐標，${\displaystyle r\ }$是點的向徑， ${\displaystyle \theta }$和 ${\displaystyle \lambda \ }$分別是點的極角和方位角

• ${\displaystyle A_{nm}}$ 和 ${\displaystyle B_{nm}}$ 是通過對單位球上的觀測數據積分確定的待定係數

• ${\displaystyle R_{nm}(\theta ,\lambda )=P_{nm}(\cos \theta )\cos {m\lambda }}$，${\displaystyle S_{nm}(\theta ,\lambda )=P_{nm}(\cos \theta )\sin {m\lambda }}$，是與締合勒讓德多項式有關的面諧函數^[23]:29

上式中的向徑 ${\displaystyle r}$ 是被計算點相對於單位球的相對半徑，而非其相對於地心的真實距離。

衛星動力學中的球諧級數

在衛星動力學中，球諧級數常寫成如下形式：^[23]:59

${\displaystyle V={GM \over r}\{{1-\sum _{n=1}^{\infty }}{\sum _{m=0}^{n}}{({a \over r})}^{n}\left[J_{nm}R_{nm}(\theta ,\lambda )+K_{nm}S_{nm}(\theta ,\lambda )\right]\}}$

上式中各個量的含義如下：

• ${\displaystyle (r,\theta ,\lambda )}$是空間中某特定點的球坐標，${\displaystyle r\ }$是空間中點的地心距離， ${\displaystyle \theta }$和 ${\displaystyle \lambda \ }$分別是點的地心緯度的餘角和經度

• ${\displaystyle GM}$ 為重力場模型的地心引力常數
• ${\displaystyle J_{nm}}$和 ${\displaystyle K_{nm}}$ 是與地球動力學有關的參數，其與 ${\displaystyle A_{nm}}$ 和 ${\displaystyle B_{nm}}$ 的關係為

${\displaystyle {\begin{cases}A_{nm}=-GMa^{n}J_{nm}\\B_{nm}=-GMa^{n}K_{nm}\end{cases}}}$

在這一表達式中，參數 ${\displaystyle A_{nm}}$、${\displaystyle B_{nm}}$、${\displaystyle J_{nm}}$和 ${\displaystyle K_{nm}}$均由地球本身的特性決定，包含了地球的轉動慣量和動力學形狀等信息，是引力場模型中的待解參數。^[23]:61-63

模型

球諧級數的示意圖，地球的引力場被視作是以上級數項的疊加

重力場模型

大地水準面是通過重力場模型進行表達的，對全球的重力場進行描述的模型即為全球重力場模型。^[46]在建立重力場模型的過程中，重力位 ${\displaystyle W}$ 被分成引力位 ${\displaystyle V}$ 和離心力位 ${\displaystyle \Phi }$ 兩部分（即 ${\displaystyle W=V+\Phi }$）， 其中離心力位 ${\displaystyle \Phi }$ 能夠根據地球的自轉角速度 ${\displaystyle \omega }$ 和點在空間中的坐標 ${\displaystyle (x,y,z)}$ 直接計算得到：^[23]:47

${\displaystyle \Phi ={1 \over 2}{\omega }^{2}(x^{2}+y^{2})}$

引力場位的確定比離心力位的確定要複雜得多，引力場模型的建立是重力場模型建立過程中的主要部分。因此，在不嚴謹的表述中，有時也將引力場模型直接稱為重力場模型。^[46]

球諧表達式

在引力場模型中，引力位 ${\displaystyle V}$ 在地球外部（${\displaystyle r>a}$）表達為如下形式：^[47]

${\displaystyle V={\frac {GM}{r}}{\sum _{n=0}^{n_{\text{max}}}}\left({\frac {a}{r}}\right)^{n}{\sum _{m=0}^{n}}{\overline {P}}_{nm}(\sin \phi )\left[{\overline {C}}_{nm}\cos m\lambda +{\overline {S}}_{nm}\sin m\lambda \right]}$

上式中的各個量的含義如下：

• ${\displaystyle (r,\phi ,\lambda )}$是空間中某特定點的球坐標，${\displaystyle r\ }$是點的地心距離， ${\displaystyle \phi \ }$和 ${\displaystyle \lambda \ }$分別是點的地心緯度和經度

• ${\displaystyle GM}$ 為重力場模型的地心引力常數
• ${\displaystyle n_{\text{max}}}$為該重力場模型的最大階數

• ${\displaystyle a}$ 為地球（參考橢球體）的長半軸
• ${\displaystyle {\overline {P}}_{nm}}$ 是 ${\displaystyle n\ }$階 ${\displaystyle m\ }$次的完全正規化締合勒讓德多項式
• ${\displaystyle {\overline {C}}_{nm}}$ 和 ${\displaystyle {\overline {S}}_{nm}}$ 是由測量數據確定的該重力場模型的完全正規化係數

其中，當 ${\displaystyle n=0}$ 時，${\displaystyle {\overline {P}}_{00}(\sin \phi )=1}$，${\displaystyle {\overline {C}}_{00}=1}$，則求和符號右側所有項的和為 ${\displaystyle 1}$；當 ${\displaystyle n=1}$ 時，${\displaystyle {\overline {C}}_{1,m}={\overline {S}}_{1,m}=0}$，則求和符號右側所有項的和為 ${\displaystyle 0}$. ^[47]因此，上式可進一步表達為如下形式：

${\displaystyle V={\frac {GM}{r}}\left(1+{\sum _{n=2}^{n_{\text{max}}}}\left({\frac {a}{r}}\right)^{n}{\sum _{m=0}^{n}}{\overline {P}}_{nm}(\sin \phi )\left[{\overline {C}}_{nm}\cos m\lambda +{\overline {S}}_{nm}\sin m\lambda \right]\right)}$

在得到引力位 ${\displaystyle V}$ 和橢球面坐標為 ${\displaystyle (r,\phi ,\lambda )}$ 的關係後，再將其與離心力位模型 ${\displaystyle \Phi }$ 相加，即可得到重力位模型 ${\displaystyle W}$，最後得到表達為 ${\displaystyle W(r,\phi ,\lambda )=W_{0}}$的大地水準面的形狀。^[23]:48 在實際的模型建立的過程中，也常取引力位中的數階最大項作為正常重力場中的引力位，再將餘下的引力位以擾動位的形式進行表達，而正常重力場中的等位面即為參考橢球面。^[8]:207-212

空間解像度

根據奈奎斯特採樣定理，球諧函數表達式中的階次越高，其表達的範圍也就越精細。對於以球諧函數來表達的重力場模型，其空間解像度通常以最短半波長表示。在地球表面，模型的空間解像度 ${\displaystyle \psi _{\text{min}}}$ 與最大階數 ${\displaystyle n_{\text{max}}}$ 的關係為：^[46]

${\displaystyle \psi _{\text{min}}={\pi R \over n_{\text{max}}}\approx {20\,000\,{\text{km}} \over n_{\text{max}}}}$

其中的${\displaystyle R}$ 為地球的平均半徑。通過這一公式，可以求出現有重力場模型常採用的空間解像度：

最大階數	最短半波長 / km
100	200.00
200	100.00
360	55.55
2190	9.13

在美國國家地理空間情報局（NGA）發佈的EGM96模型中，${\displaystyle n_{\text{max}}=360}$，即該模型給出了最高完全階次至360的重力場模型係數，其表達的大地水準面的解像度可達55千米或110千米（取決於對解像度定義的不同）。而在2009年，NGA又發佈了最大階數 ${\displaystyle n_{\text{max}}=2190}$，最高完全階次為2159次的EGM08模型，其大地水準面的解像度可達12千米，精度在全球範圍內可達±15厘米。^[48][12]

現有的地球重力場模型

現有的地球重力場模型由國際地球重力場模型中心（ICGEM）負責收集和存檔。^[49]截至2020年，ICGEM存儲的階數超過2000階的超高階靜態全球重力場模型有如下幾個：

模型	發佈時間	最高階數	數據來源	參考文獻
EGM2008	2009年	2190	A、G、S(Grace)	[48]
EIGEN-6C4	2014年	2190	A、G、S(Goce、Grace、Lageos)	[50]
GECO	2015年	2190	EGM2008、S(Goce)	[51]
SGG-UGM-1	2018年	2159	EGM2008、S(Goce)	[52]
XGM2019e_2159	2019年	760/2190/5540	A、G、S(GOCO06s)、T	[53]
註：其中A表示測高數據，S表示為衛星測量數據，G表示地表測量數據（包括陸地、船舶和航空測量），T表示測圖數據

高程系統

橢球高h、大地水準面高N和正高H的示意圖，圖中紅色實線為大地水準面（Geoid），黑色虛線為橢球面（Ellipsoid），注意圖中的N實際上是N的絕對值

主條目：正高

大地水準面是正高系統的參考面，正高被定義為地面上任意一點沿其所在的鉛垂線到大地水準面的距離。^[23]:166在重力水準測量中，觀測到大地水準面上一點 ${\displaystyle O}$ 與任意一點 ${\displaystyle B}$ 之間的重力位差${\displaystyle {\begin{smallmatrix}\int \limits _{OB}g\operatorname {d} \!h\end{smallmatrix}}}$，再求得點 ${\displaystyle B}$ 沿鉛垂線到大地水準面的路徑上的重力平均值 ${\displaystyle g_{\text{m}}^{B}}$，可計算得點 ${\displaystyle B}$ 的正高為：^[10]:42

${\displaystyle H^{B}={1 \over g_{\text{m}}^{B}}\int \limits _{OB}g\operatorname {d} \!h}$

一個正高系統必須與一個重力位已知的大地水準面相聯繫，這個重力位即為大地水準面重力位。

與大地高的關係

在大地測量學以外的領域，正高也被稱為海拔高度。^[23]:172而在進行空間位置的計算（如計算GPS等全球衛星導航系統中的衛星位置）時，使用的高度則是相對於參考橢球面的距離，稱為大地高或橢球高。兩者間的轉換需要通過大地水準面高進行：^[54]

${\displaystyle h=H+N}$

其中，${\displaystyle h}$ 表示大地高（橢球高），${\displaystyle H}$ 表示正高，${\displaystyle N}$ 表示大地水準面高。

與正常高的關係

主條目：正常高

正高的計算需要用到重力平均值 ${\displaystyle g_{\text{m}}^{B}}$，但該值無法在地球內部的質量和重力分佈未知的情況下得到，所以正高無法被精確求得。^[8]:3511945年，蘇聯大地測量學家莫洛堅斯基提出了利用正常高來代替正高的計算方式。^[55]在這一高程系統中，由地球表面向下量取正常高而獲得的表面被稱為似大地水準面，由正常橢球面向上量取正常高而獲得的表面則被稱為似地形表面，而似大地水準面和正常橢球面之間的差距又被稱為高程異常。^[56]似大地水準面與水準面不同，它沒有具體的物理意義，更不是重力等位面，只是用於計算的輔助面。^[23]:294大地水準面和似大地水準面在山區的差異可達4米，但兩者在平均海水面上是重合的。^[8]:352

大地水準面重力位

大地水準面重力位 ${\displaystyle W_{0}}$ 與高程基準相互對應，是人為規定的參考值。這一參考值應具有不隨時間變化、長期固定，且與平均海水面的高度有明確關係的特徵。^[57]在2015年，國際大地測量協會（IAG）公佈的大地水準面重力位參考值為${\displaystyle W_{0}=6.263\,685\,34\times 10^{7}\,{\text{m}}^{2}\cdot {\text{s}}^{-2}}$。^[58][59]但在不同的區域高程系統中，其定義的高程系統仍可能對應出不同的大地水準面重力位值。以中國1985國家高程基準為例，其與全球平均大地水準面的差異為21到23厘米。^[60]

時變現象

在加拿大、北歐和南極洲等地，冰後回彈效應會使得大地水準面發生每年多達2毫米的變化，垂直方向上的地殼構造運動亦會使大地水準面發生微小的變動。^[61]:170-171在建立高精度的高程系統時候，考慮這些大地水準面的時變現象是非常有必要的。^[62]:24重力測量衛星可以用於這類時變現象的監測。以GRACE衛星為例，其對長波時變重力場的時間解像度可達10天，測定的大地水準面年變化率精度為0.01毫米每年。^[63]

相關條目

• 地球科學主題

• 地球引力

• 布隆斯公式

• 大地測量系統

註釋

1. 儘管「重力」和「引力」在其他場合經常混用，但在研究地球重力場時，「重力」專指由地球質量產生的「萬有引力」和由地球自轉產生的離心慣性力的合力。^[2]

參考文獻

1. WGS 84, N=M=180 Earth Gravitational Model. NGA: Office of Geomatics. National Geospatial-Intelligence Agency. [2016-12-17]. （原始內容存檔於2020-08-08） （英語）.
2. gravitational force - 重力，引力. 國家教育研究院. [2020-04-16]. （原始內容存檔於2017-07-08）.
3. Gauss, Carl Friedrich. Bestimmung des Breitenunterschiedes zwischen den Sternwarten von Göttingen und Altona: durch Beobachtungen am Ramsdenschen Zenithsector. Bei Vandenhoeck und Ruprecht. 1828 [2020-04-06]. （原始內容存檔於2020-08-21） （德語）.
4. Torge, Wolfgang. Geodesy. Walter de Gruyter GmbH & Co KG. 2015-08-31 [2020-04-06]. ISBN 978-3-11-154268-3. （原始內容存檔於2020-08-21） （英語）.
5. Vanicek, Mr Petr; Christou, Nikolaos T. Geoid and its Geophysical Interpretations. CRC Press. 1993-10-18 [2020-04-06]. ISBN 978-0-8493-4227-1. （原始內容存檔於2020-08-21） （英語）.
6. Freeden, Willi; Nashed, M. Zuhair. Handbook of Mathematical Geodesy: Functional Analytic and Potential Theoretic Methods. Birkhäuser. 2018-06-11 [2020-04-10]. ISBN 978-3-319-57181-2. （原始內容存檔於2020-08-21） （英語）.
7. Johann B., Listing. Über unsere jetzige Kenntnis der Gestalt und Größe der Erde : Enth.: Neue geometrische und dynamische Constanten des Erdkörpers. Gottingen. 1873 （德語）.
8. 寧津生. 管澤霖 , 編. 地球形状及外部重力场. 測繪出版社. 1981: 154–293.
9. GRACE - Gravity Recovery and Climate Experiment. www2.csr.utexas.edu. [2020-04-06]. （原始內容存檔於2019-02-06）.
10. 孔祥元; 郭際明; 劉宗泉. 大地测量学基础. 武漢大學出版社. 2001. ISBN 978-7-30-707562-7.
11. Geoid - The concept of the geoid. Encyclopedia Britannica. [2020-04-09]. （原始內容存檔於2021-02-15） （英語）.
12. 寧津生; 王正濤. 地球重力场研究现状与进展. 測繪地理信息. 2013, (01): 1-7 [2020-04-07]. ISSN 1007-3817. doi:10.14188/j.2095-6045.2013.01.012. （原始內容存檔於2020-08-21）.
13. 潘正風; 程效軍; 成樞; 王騰軍; 翟翊. 数字地形测量学. 武漢大學出版社. 2015-07-01. ISBN 978-7-307-15677-7.
14. CHAPTER V PHYSICAL GEODESY. www.ngs.noaa.gov. [2020-04-06]. （原始內容存檔於2020-08-08）.
15. Lanzano, Paolo (編). Chapter I Concepts of Physical Geodesy. International Geophysics. Deformations of an Elastic Earth 31. Academic Press. 1982-01-01: 1–40 [2020-04-06]. doi:10.1016/s0074-6142(08)60467-2. （原始內容存檔於2020-08-08） （英語）.
16. Xiong Li; Hans-Jürgen Götze. GEOPHYSICS (PDF). web.archive.org. 2011-01-13 [2020-04-08]. 原始內容存檔於2011-01-13. 引文使用過時參數coauthors (幫助)
17. Rapp, Richard H. The geoid: Definition and determination. Eos, Transactions American Geophysical Union. 1974, 55 (3): 118–126 [2020-04-08]. ISSN 2324-9250. doi:10.1029/EO055i003p00118. （原始內容存檔於2020-08-21） （英語）.
18. 申文斌; 寧津生; 李建成; 晁定波. 论大地水准面. 武漢大學學報（信息科學版）. 2003, (06): 683-687 [2020-04-08]. （原始內容存檔於2020-08-08）.
19. Rapp, Richard H. The determination of geoid undulations and gravity anomalies from SEASAT altimeter data. Journal of Geophysical Research: Oceans. 2012-09-20: 1552–1562 [2020-04-08]. ISSN 2169-9275. doi:10.1029/JC088iC03p01552@10.1002/(ISSN)2169-9291.SEASAT2. （原始內容存檔於2020-08-21）.
20. Mather, R. S. The role of the geoid in four‐dimensional geodesy. Marine Geodesy. 1978-01-01, 1 (3): 217–252. ISSN 0149-0419. doi:10.1080/01490417809387968.
21. Bjerhammar, Arne. On a relativistic geodesy. Bulletin géodésique. 1985-09-01, 59 (3): 207–220. ISSN 1432-1394. doi:10.1007/BF02520327 （英語）.
22. Philipp, Dennis; Hackmann, Eva; Lämmerzahl, Claus; Müller, Jürgen. Relativistic geoid: Gravity potential and relativistic effects. Physical Review D. 2020-03-17, 101 (6): 064032. ISSN 2470-0010. doi:10.1103/PhysRevD.101.064032 （英語）.
23. San Francisco W. H. Freeman and Company. Heiskanen Moritz 1967 Physical Geodesy. San Francisco: W. H. Freeman and Company. 1967 （英語）. 引文格式1維護：日期與年 (link)
24. NGA: DoD World Geodetic System 1984. earth-info.nga.mil. [2020-04-06]. （原始內容存檔於2021-01-26）.
25. Castelvecchi, Davide. The Geoid: Why a map of Earth's gravity yields a potato-shaped planet. Scientific American Blog Network. [2020-04-06]. （原始內容存檔於2020-11-12） （英語）.
26. The Geoid. www.usna.edu. [2020-04-09]. （原始內容存檔於2020-08-08）.
27. Richards, Mark A.; Hager, Bradford H. Geoid anomalies in a dynamic Earth. Journal of Geophysical Research: Solid Earth. 1984, 89 (B7): 5987–6002 [2020-04-08]. ISSN 2156-2202. doi:10.1029/JB089iB07p05987. （原始內容存檔於2020-08-21） （英語）.
28. 樓立志. 中国及邻区模拟大地水准面的研究 (Ph.D.論文). 中國科學院研究生院（測量與地球物理研究所）. 2004 [2020-04-08]. （原始內容存檔於2020-08-08）.
29. Chase, Clement G. Subduction, the geoid, and lower mantle convection. Nature. 1979-11, 282 (5738): 464–468 [2020-04-08]. ISSN 0028-0836. doi:10.1038/282464a0. （原始內容存檔於2020-09-22） （英語）.
30. Crough, S. Thomas; Jurdy, Donna M. Subducted lithosphere, hotspots, and the geoid. Earth and Planetary Science Letters. 1980-06-01, 48 (1): 15–22. ISSN 0012-821X. doi:10.1016/0012-821X(80)90165-X （英語）.
31. Anderson, Don L. Hotspots, polar wander, Mesozoic convection and the geoid. Nature. 1982-06, 297 (5865): 391–393 [2020-04-08]. ISSN 1476-4687. doi:10.1038/297391a0. （原始內容存檔於2020-10-29） （英語）.
32. Mishra, D. C.; Ravi Kumar, M. Long and short wavelengths of Indian Ocean geoid and gravity lows: Mid-to-upper mantle sources, rapid drift and seismicity of Kachchh and Shillong plateau, India. Journal of Asian Earth Sciences. 2012-10-22, 60: 212–224. ISSN 1367-9120. doi:10.1016/j.jseaes.2012.08.024 （英語）.
33. Mishra, D.C. Geoid low and highs of the Indian Ocean and Western Pacific: Implications to mantle convection. Journal of Asian Earth Sciences. 2014-01-05, 79: 441–445. doi:10.1016/j.jseaes.2013.10.020.
34. Negi, J. G.; Thakur, N. K.; Agrawal, P. K. Can depression of the core-mantle interface cause coincident Magsat and geoidal ‘lows’ of the Central Indian Ocean?. Physics of the Earth and Planetary Interiors. 1987-01-01, 45 (1): 68–74. ISSN 0031-9201. doi:10.1016/0031-9201(87)90198-1 （英語）.
35. Reiss, Anne-Sophie; Thomas, Christine; van Driel, Jac; Heyn, Björn. A hot midmantle anomaly in the area of the Indian Ocean Geoid Low: Hot Anomaly Below IOGL. Geophysical Research Letters. 2017-07-16, 44 (13): 6702–6711. doi:10.1002/2017GL073440 （英語）.
36. 寧津生; 羅志才; 李建成. 大地测量与地球动力学. 大地測量與地球動力學. 2004, 24 (01): 4-8 [2020-04-10]. ISSN 1003-4137. （原始內容存檔於2020-08-08）.
37. 陳俊勇; 李建成; 寧津生; 晁定波; 張燕平; 張驥. 中国新一代高精度、高分辨率大地水准面的研究和实施. 武漢大學學報(信息科學版). 2001, (04): 283-289+302 [2020-04-10]. （原始內容存檔於2020-08-08）.
38. 寧津生. 卫星重力探测技术与地球重力场研究. 大地測量與地球動力學. 2002, 22 (1): 1–5 [2020-04-09]. （原始內容存檔於2020-08-21）.
39. 寧津生. 地球重力场逼近理论研究进展. 武漢測繪科技大學學報. 1998, (04): 31-34+7 [2020-04-10]. （原始內容存檔於2020-08-08）.
40. Merson, R. H.; King-Hele, D. G. Use of Artificial Satellites to Explore the Earth's Gravitational Field: Results from Sputnik 2 (1957β). Nature. 1958-09, 182 (4636): 640–641 [2020-04-10]. ISSN 1476-4687. doi:10.1038/182640a0. （原始內容存檔於2020-10-29） （英語）.
41. ESA makes first GOCE dataset available. GOCE. European Space Agency. 9 June 2010 [22 December 2016]. （原始內容存檔於2012-10-20）.
42. GOCE giving new insights into Earth's gravity. GOCE. European Space Agency. 29 June 2010 [22 December 2016]. （原始內容存檔於2010-07-02）.
43. Stokes, George Gabriel. On the Variation of Gravity at the Surface of the Earth. Mathematical and Physical Papers. 2009/07 [2020-04-06]. （原始內容存檔於2020-08-08） （英語）. 請檢查|date=中的日期值 (幫助)
44. Survey, U. S. Coast and Geodetic; Lambert, Walter Davis; Darling, Frederic Warren. Tables for Determining the Form of the Geoid and Its Indirect Effect on Gravity. U.S. Government Printing Office. 1936 [2020-04-07]. （原始內容存檔於2020-08-21） （英語）.
45. 寧津生. 管澤霖 , 編. 地球形状及外部重力场：下册. 測繪出版社. 1981: 154–293.
46. ICGEM Service Frequently Asked Questions (FAQs) (PDF). [2020-04-08]. （原始內容存檔 (PDF)於2020-05-03） （英語）.
47. There is no such thing as "The" EGM96 geoid: Subtle points on the use of a global geopotential model.. www.ngs.noaa.gov. [2020-04-06]. （原始內容存檔於2016-03-04）.
48. NGA: EGM2008 - WGS 84 Version. earth-info.nga.mil. [2020-04-07]. （原始內容存檔於2021-02-24）.
49. Franz Barthelmes, Elmas Sinem Ince, Sven Reißland. ICGEM International Center for Global Gravity Field Models. icgem.gfz-potsdam.de. [2020-04-07]. （原始內容存檔於2021-02-13）.
50. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. dataservices.gfz-potsdam.de. [2020-04-07]. （原始內容存檔於2020-08-15） （英國英語）.
51. Gilardoni, Maddalena; Reguzzoni, Mirko; Sampietro, Daniele. GECO: a global gravity model by locally combining GOCE data and EGM2008. Studia Geophysica et Geodaetica. 2016-04-01, 60 (2): 228–247. ISSN 1573-1626. doi:10.1007/s11200-015-1114-4 （英語）.
52. Xu, Xinyu; Zhao, Yongqi; Reubelt, Tilo; Tenzer, Robert. A GOCE only gravity model GOSG01S and the validation of GOCE related satellite gravity models. Geodesy and Geodynamics. 2017-07-01, 8 (4): 260–272 [2020-04-07]. ISSN 1674-9847. doi:10.1016/j.geog.2017.03.013. （原始內容存檔於2020-11-25） （英語）.
53. The experimental gravity field model XGM2019e. dataservices.gfz-potsdam.de. [2020-04-07]. （原始內容存檔於2020-08-08） （英國英語）.
54. Converting GPS Height into NAVD88 Elevation with the GEOID96 Geoid Height Model. www.ngs.noaa.gov. [2020-04-06]. （原始內容存檔於2018-09-16）.
55. Molodensky, M. S. Fundamental Problems of Geodetic Gravimetry. TRUDY Ts NIIGAiK. 1945, (42).
56. Vaníček, Petr; Kingdon, Robert; Santos, Marcelo. Geoid versus quasigeoid: a case of physics versus geometry. Contributions to Geophysics and Geodesy. 2012-01-01, 42 (1): 101–118 [2020-04-07]. ISSN 1335-2806. doi:10.2478/v10126-012-0004-9. （原始內容存檔於2020-08-21） （英語）.
57. Sánchez, L.; Čunderlík, R.; Dayoub, N.; Mikula, K.; Minarechová, Z.; Šíma, Z.; Vatrt, V.; Vojtíšková, M. A conventional value for the geoid reference potential $$W_{0}$$W0. Journal of Geodesy. 2016-09-01, 90 (9): 815–835. ISSN 1432-1394. doi:10.1007/s00190-016-0913-x （英語）.
58. IAG Resolutions (pdf). [2020-04-09]. （原始內容存檔 (PDF)於2020-09-20） （英語）.
59. Freymueller, Jeffrey T.; Sánchez, Laura. International Symposium on Advancing Geodesy in a Changing World: Proceedings of the IAG Scientific Assembly, Kobe, Japan, July 30 – August 4, 2017. Springer. 2019-03-12 [2020-04-09]. ISBN 978-3-030-12915-6. （原始內容存檔於2020-08-21） （英語）.
60. 李建成, 褚永海; LI Jiancheng, CHU Yonghai. 区域与全球高程基准差异的确定. 測繪學報. 2017-10-20, 46 (10): 1262 [2020-04-08]. ISSN 1001-1595. doi:10.11947/j.AGCS.2017.20170538. （原始內容存檔於2020-08-21） （中文）.
61. Watts, Anthony B. Treatise on Geophysics, Volume 6: Crust and Lithosphere Dynamics. Elsevier. 2010-05-13 [2020-04-10]. ISBN 978-0-444-53572-6. （原始內容存檔於2020-08-21） （英語）.
62. Flury, Jakob; Rummel, Reiner. Future Satellite Gravimetry and Earth Dynamics. Springer Science & Business Media. 2007-01-25 [2020-04-10]. ISBN 978-0-387-33185-0. （原始內容存檔於2020-08-21） （英語）.
63. 晁定波. 论高精度卫星重力场模型和厘米级区域大地水准面的确定及水文学时变重力效应. 測繪科學. 2006, (06): 16-18+23+3 [2020-04-08]. ISSN 1009-2307. （原始內容存檔於2020-11-23）.

延伸閱讀

• 海斯卡寧·莫里茨 1967年版物理大地測量學（Heiskanen Moritz 1967 Physical Geodesy）（英語）
• 沃爾夫岡·托爾格 大地測量學第二版 （Wolfgang Torge Geodesy） （頁面存檔備份，存於互聯網檔案館）（英語）

外部連結

• EGM96地球重力場模型（頁面存檔備份，存於互聯網檔案館）（英語）
• EGM08地球重力場模型（頁面存檔備份，存於互聯網檔案館）（英語）
• 國際地球重力場模型中心（ICGEM） （頁面存檔備份，存於互聯網檔案館）（英語）
• 國際大地水準面服務（ISG） （頁面存檔備份，存於互聯網檔案館）（英語）
• 美國國家海洋和大氣管理局（NOAA） （頁面存檔備份，存於互聯網檔案館）（英語）
• 橢球面、大地水準面、重力、大地測量學和地球物理學教程（Tutorial Ellipsoid, geoid, gravity, geodesy, and geophysics）（英語）
• GRACE網站上對確定地球重力方法的闡述（頁面存檔備份，存於互聯網檔案館）（英語）