平賭 (機率論)
概率論的一種隨機過程 来自维基百科,自由的百科全书
在機率論中,平賭(英語:martingale)是滿足下述條件的隨機過程:已知過去某一 時刻 s 以及之前所有時刻的觀測值,若某一時刻 t 的觀測值的條件期望等於過去某一時刻 s 的觀測值,則稱這一隨機過程是平賭。而於博弈論中,平賭經常用來作為公平博弈的數學模型。
歷史

鞅的原名「martingale」原指一類於18世紀流行於法國的投注策略,稱為加倍賭注法[1]。這類策略中最簡單的一種策略是為博弈設計的。在博弈中,賭徒會擲硬幣,若硬幣正面向上,賭徒會贏得賭本,若硬幣反面向上,賭徒會輸掉賭本。這一策略使賭徒在輸錢後加倍賭金投注,為的是在初次贏錢時贏回之前輸掉的所有錢,同時又能另外贏得與最初賭本等值的收益。當賭徒的財產和可用時間同時接近無窮時,他擲硬幣後硬幣正面向上的概率會接近1,由此看來,加倍賭注法似乎是一種必然能贏錢的策略。然而,由於現實中賭徒的資金是有限的,賭金的指數增長最終會導致使用這一策略的賭徒破產。
鞅的概念首先是由保羅·皮埃爾·萊維於1934年提出的,但他只提出了離散時間的版本,而且沒有給予命名。直到1939年,約翰·維爾將此概念推廣到連續時間的情況,並且首次提出「martingale」這個名稱。約瑟夫·利奧·杜布等人在鞅的相關理論的初期發展做出重大貢獻,而完成這些工作的部分動機是為了表明成功的投注策略不可能存在。此外,伊藤清在分析應用方面作出了重要的貢獻。從1970年代開始,鞅論就在純粹數學和應用數學的很多領域中有廣泛的應用,特別是在數學物理和金融數學中。
定義
離散時間鞅是對於所有 n 都滿足
的時間離散的隨機過程 X1,X2,X3,…,也就是說,已知之前所有觀測值,若下一次觀測值的條件期望等於本次觀測值,則稱這一隨機過程(即隨機變量序列)是離散時間鞅。
相對來說更為一般的定義如下:若對於所有 n 都滿足
則稱隨機過程 Y1,Y2,Y3,…是關於另一隨機過程 X1,X2,X3,…的鞅。
與離散時間鞅的定義相似,連續時間鞅的定義為:若對於所有 t 都滿足
則稱關於隨機過程 Xt 的連續時間鞅是隨機過程 Yt 。
上述定義表達了鞅的性質,即在 s ≤ t 的條件下,已知時刻 s 以及之前所有時刻的觀測值,若時刻 t 的觀測值的條件期望等於時刻 s 的觀測值,則隨機過程是鞅。
更為一般性的定義如下:若隨機過程 滿足如下性質,則稱 Y 是一個關於濾鏈 Σ∗和概率測度 P 的鞅。
- Σ∗ 是給定機率空間 (Ω, Σ, P) 的濾鏈;
- Y 是適應於濾鏈 Σ∗ 的適應過程,即對於指標集 T 中的每一 t ,隨機變量 Yt 是一個 Σt 可測函數;
- 對於任意 t ,Yt 存在於 Lp 空間 L1(Ω, Σt, P; S) 中,即
- 對於所有 s 和 t (s < t )和所有 F ∈ Σs,
- 其中 χF 表示事件 F 的指示函數。在 Grimmett 和 Stirzaker 的《Probability and Random Processes》一書中,最後一個條件被表示為條件期望的一般形式[2]:
要注意的重點是鞅成立的性質與濾鏈以及關於選定期望的機率測度都有關。Y 可能是某一測度的鞅,但不是另一測度的鞅;而要說明某一伊藤過程是鞅,則可以利用吉爾薩諾夫定理找出相關的測度。
鞅的例子
- 設 Xn 是一個賭徒 n 次拋擲公平硬幣後的財產,規則是如果硬幣正面朝上,則賭徒贏得 1 美元,硬幣反面朝上,則賭徒輸掉 1 美元。在已知過去不同時刻所擁有的財產之下,下一次試驗後賭徒財產的條件期望與其現在的財產相等,故這一隨機過程是鞅。這個例子稱為賭徒謬誤。
- 令 Yn = Xn2 − n ,其中 Xn 是上例中賭徒的財產,則隨機過程{ Yn : n = 1, 2, 3, ... }是鞅。這一例子可以表明賭徒的全部收益或損失大致在拋擲次數的正負平方根之間變化。
- (棣莫弗鞅)設拋擲的是有偏硬幣(或稱為不公平硬幣),正面向上的概率為 p,反面向上的概率為 q = 1 − p 。令
- 正面情況用「+」,反面情況用「−」。令
- 則{ Yn : n = 1, 2, 3, ... }是關於{ Xn : n = 1, 2, 3, ... }的鞅。證明如下:

- (波利亞罐子模型)一個罐子中最初裝有 r 個紅球和 b 個藍球。某人隨機取出一個球,然後將此球與另一個與此球顏色相同的球放回罐子中。令 Xn 為重複上述步驟 n 次後罐子中的紅球數,令 Yn = Xn / (n + r + b)。這時隨機過程{ Yn : n = 1, 2, 3, ... }是鞅。
- (統計學中的似然比檢驗)某一總體可能是按照概率密度 f 分布,也可能是按照概率密度 g 分布。從總體中取出一個隨機樣本,數據為 X1, ..., Xn 。令 Yn 為「似然比」:
- (上式在應用中用作檢驗統計量。)若總體實際上是按照概率密度 f 而不是 g 分布,則{ Yn : n = 1, 2, 3, ... }是關於{ Xn : n = 1, 2, 3, ... }的鞅。
- 設每一變形蟲不是以概率 p 分裂成兩個變形蟲,就是以概率 1 − p 最終死亡。令 Xn 為 n 代後變形蟲的存活數目(若種群在某一時刻滅絕,則這一時刻的 Xn = 0)。令 r 為最終滅絕的概率。(找出 r 關於 p 的函數在實際應用中是非常有用的。提示:已知最初的一個變形蟲已經分裂了,則這個變形蟲的後代最終滅絕的概率等於其分裂直接得到的兩個後代中任何一個死亡的概率。)則
- 是關於{ Xn : n = 1, 2, 3, ... }的鞅。

- 一個大小固定生態系統中,任一特定物種的個體數量都是一個(離散)時間函數,可被視為一個隨機過程(隨機變量序列)。這一隨機過程是生物多樣性和生物地理學的統一中性理論下的鞅。
- 利用計算機軟件,鞅序列可以很容易地製作出來:
- Microsoft Excel或類似的電子製表軟件:在A1(左上角)單元格中輸入0.0,在下方的A2單元格中輸入
=A1+NORMINV(RAND(),0,1)。這時下拉複製此單元格,得到大約300個單元格,這樣就能創建均值為0,標準差為1的鞅序列。在這些單元格仍處於選中狀態的情況下,利用圖表創建工具創建這些值的圖表。這時每次重新計算後(在Excel中可按F9實現),圖表都會顯示出不同的鞅序列。 - R語言:若要再現上述例子,可運行如下命令。若要顯示另一個鞅,重新輸入如下命令即可。
plot(cumsum(rnorm(100, mean=0, sd=1)), t="l", col="darkblue", lwd=3)
- Microsoft Excel或類似的電子製表軟件:在A1(左上角)單元格中輸入0.0,在下方的A2單元格中輸入
下鞅與上鞅
(離散時間)下鞅(submartingale,又稱亞鞅)是滿足
的可積隨機過程 X1,X2,X3,…。
類似地,(離散時間)上鞅(supermartingale,又稱超鞅)是滿足
的可積隨機過程 X1,X2,X3,…。
下鞅或上鞅的定義都可由前述的離散時間和連續時間鞅的更為一般的定義轉換得到,只需將條件期望的等式代換成不等式即可。
這裡給出一個區分下鞅和上鞅的記憶方法:「生活是一個上鞅:隨着時間的推進,期望降低。」
- 每一個鞅既是下鞅又是上鞅,反過來任何既是下鞅又是上鞅的隨機過程是鞅。
- 再次考慮賭徒的例子,若硬幣正面向上,賭徒贏得1美元,若硬幣反面向上,賭徒輸掉1美元。設此時硬幣是有偏的,則硬幣正面向上的概率為p 。
- 若 p 等於 1/2,平均起來,賭徒既未贏錢也未輸錢,則隨着時間的流逝,賭徒的財產是一個鞅。
- 若 p 小於 1/2,平均起來,賭徒輸了錢,則隨着時間的流逝,賭徒的財產是一個上鞅。
- 若 p 大於 1/2,平均起來,賭徒贏了錢,則隨着時間的流逝,賭徒的財產是一個下鞅。
- 由延森不等式求出的鞅的凸函數(convex function)是下鞅。例如,公平硬幣博弈中賭徒財產的平方是下鞅(同時也是根據 Xn2 − n 是鞅的事實得出的)。類似地,鞅的凹函數(concave function)是一個上鞅。
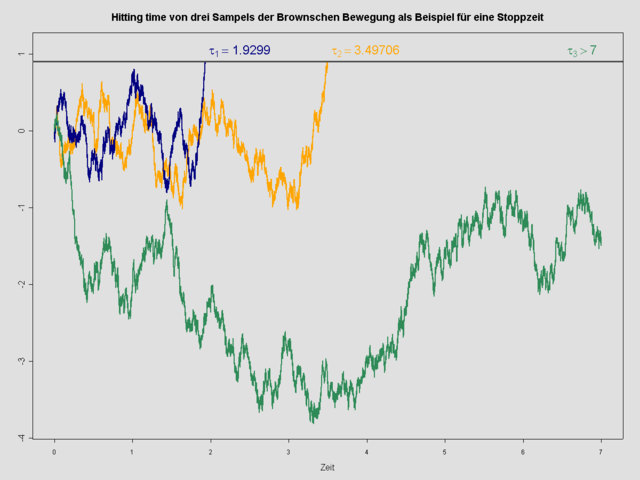
鞅與停時
關於隨機過程 X1,X2,X3,… 的停時是隨機變量 τ,這一隨機變量具有如下性質:對於每一個時間 ,事件 τ = t 的發生與否僅取決於 X1,X2,X3,…,Xt 的取值。從定義中可以感受到的直覺是在任一特定時刻 t,我們都可以知道在這一時刻隨機過程是否到了停時。現實生活中停時的例子如賭徒離開賭桌的時刻,這一時刻可能是賭徒以前贏得錢財的函數(例如,僅當他沒有錢時,他才可能離開賭桌),但是他不可能根據還未完成的博弈的結果來選擇離開還是留下。
上述停時定義滿足強條件,下面給出一個弱條件的停時定義:若事件 τ = t 的發生與否統計獨立於 Xt+1,Xt+2,… 但並不是完全決定於時刻 t 以及之前的過程歷史,則隨機變量 τ 是停時。雖然這是一個弱條件,但在需要用到停時的證明中的一些情況也算是足夠強的條件。
鞅的一個基本性質是若是下\上鞅且 是停時,由 定義的對應停止過程 也是下\上鞅。
停時鞅的概念引出了一系列定理,例如可選停止定理(又稱可選抽樣定理):在特定條件下,停時的鞅的期望值等於其初始值。利用這一定理,我們可以證明對於一個壽命有限且房產有限的賭徒,成功的投注策略不可能存在。
參見
參考文獻
Wikiwand - on
Seamless Wikipedia browsing. On steroids.









![{\displaystyle \mathbf {E} _{\mathbf {P} }\left([Y_{t}-Y_{s}]\chi _{F}\right)=0,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5a839e72c46650c7da597b2e583a3677e9c960fd)



![{\displaystyle {\begin{aligned}E[Y_{n+1}\mid X_{1},\dots ,X_{n}]&=p(q/p)^{X_{n}+1}+q(q/p)^{X_{n}-1}\\&=p(q/p)(q/p)^{X_{n}}+q(p/q)(q/p)^{X_{n}}\\&=q(q/p)^{X_{n}}+p(q/p)^{X_{n}}=(q/p)^{X_{n}}=Y_{n}.\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5d39ca9848fbe72736ccddbfe499d0a07ce32f22)



![{\displaystyle {}E[X_{n+1}|X_{1},\ldots ,X_{n}]\geq X_{n},\quad n\in \mathbb {N} }](http://wikimedia.org/api/rest_v1/media/math/render/svg/ad18070dbd7931e5cad0c2cef27a40d8ca2c570b)
![{\displaystyle {}E[X_{n+1}|X_{1},\ldots ,X_{n}]\leq X_{n},\quad n\in \mathbb {N} }](http://wikimedia.org/api/rest_v1/media/math/render/svg/dd6a06fa6e84991c5ad6af44f634f678c450e43d)



