Loading AI tools
персидский астроном Из Википедии, свободной энциклопедии
Насир ад-Ди́н Абу́ Джафар Муха́ммад ибн Муха́ммад Ту́си́[комм. 1] (перс. محمد بن محمد بن الحسن الطوسی, 18 февраля 1201[1][2], Тус, Низаритское исмаилитское государство[3][1] — 26 июня 1274[1][2], Кадимия[вд], Багдад, Государство Хулагуидов[1]) — персидский[5][6][7][8][9][10][11][12][13] математик, механик и астроном XIII века[14], ученик Камал ад-Дина ибн Юниса, чрезвычайно разносторонний учёный, автор сочинений по философии, географии, музыке, оптике, медицине, минералогии. Был знатоком греческой науки, комментировал труды Евклида, Архимеда, Автолика, Феодосия, Менелая, Аполлония, Аристарха, Гипсикла, Птолемея.
| Насир ад-Дин ат-Туси | |
|---|---|
| محمد بن محمد بن الحسن الطوسی | |
 Насир ад-Дин Туси (сидит за столом) в Марагинской обсерватории. Миниатюра 1562 года. Британская библиотека | |
| Имя при рождении | араб. مُحمد بن مُحمد بن الحسن الطُوسي |
| Дата рождения | 18 февраля 1201[1][2] |
| Место рождения | |
| Дата смерти | 26 июня 1274[1][2] (73 года) |
| Место смерти | |
| Страна | |
| Род деятельности | философ, учёный, математик, астроном, астролог, универсальный человек, архитектор, врач, даи, богослов, марджа ат-таклид, поэт, переводчик, писатель, автор, политик |
| Научная сфера | астрономия, математика, философия, география, музыка, оптика, медицина, минералогия |
| Место работы | |
| Научный руководитель | Ибн Юнис, Камал ад-Дин |
| Ученики | Абд аль-Карим ибн Тавус[вд], Ал-Казвини, Аш-Ширази, Алламе Хилли, Ибн аль-Фувати[вд], Шамс ад-Дин аль-Бухари[вд][4] и Q5727970? |
Известно около 150 трактатов и писем Насир ад-Дина ат-Туси, из которых двадцать пять написаны на персидском, а остальные — на арабском языке. Существует даже трактат по геомантии, который Туси написал на арабском, персидском и тюркском, демонстрируя своё мастерство на всех трёх языках. Отмечается, что Туси знал и греческий[15].
Насир ад-Дин ат-Туси родился в городе Тус области Хорасан на северо-востоке Ирана в 1201 году[14]. Там же в раннем возрасте он начал учёбу, изучив Коран, хадисы, шиитскую юриспруденцию, логику, философию, математику, медицину и астрономию[16]. Позже продолжил обучение астрономии и математике в Мосуле у Камал ад-Дина ибн Юниса.
Первый период деятельности ат-Туси связан с Кухистаном, где ему покровительствовал наместник халифа. Позже учёный впал в немилость и с 1235 года жил в крепости Аламут, резиденции главы государства исмаилитов-низаритов. Ат-Туси возглавлял промонгольскую партию и был причастен к сдаче Аламута монголам в 1256 году. Царевич, а впоследствии ильхан, Хулагу осыпал ат-Туси милостями и сделал своим придворным астрологом. В 1258 году ат-Туси участвовал в походе Хулагу на Багдад и вёл переговоры с халифом о капитуляции. В течение многих лет ат-Туси был советником Хулагу по финансовым вопросам; он разработал проект налоговой реформы, осуществлённый одним из преемников ильхана.
Среди математических трудов ат-Туси особенно значителен «Трактат о полном четырёхстороннике» (в другом переводе — «Трактат о фигуре секущих»). Трактат был написан по-персидски во время пребывания ат-Туси в Аламуте и по-арабски, в несколько сокращённом виде, в Мараге (1260). В качестве своего основного предшественника ат-Туси указывает на аль-Бируни с его «Книгой ключей науки астрономии о том, что происходит на поверхности сферы». В трактате упоминается трактат ас-Салара по этому же вопросу, причём в персидской версии почтительно, а в арабской — уничижительно, что, по-видимому, было связано с борьбой ат-Туси против ас-Салара при дворе Хулагу. Сочинение ат-Туси послужило одним из источников для Региомонтана (1436—1476), с именем которого связано начало нового этапа в истории тригонометрии.
Трактат ат-Туси состоит из пяти книг. В I книге изложена теория составных отношений. Развивая идеи Сабита ибн Корры и Омара Хайяма, ат-Туси вводит здесь расширенное понятие числа, которое определяется как отношение, рациональное или иррациональное. Во II книге даются доказательства различных случаев теоремы Менелая для плоского четырёхсторонника. В III книге вводятся понятия синуса и косинуса дуги и доказывается ряд теорем плоской тригонометрии; в частности, здесь рассматриваются правила решения плоских треугольников и дано доказательство плоской теоремы синусов. Книга IV посвящена доказательству различных случаев теоремы Менелая для сферической фигуры секущих. В V книге рассматриваются приемы решения задач сферической тригонометрии с помощью теорем, «заменяющих фигуру секущих», — теоремы тангенсов и теоремы синусов. В заключительной главе V книги предлагаются правила решения сферических треугольников, причём для того случая, когда в треугольнике даны три угла, вводится понятие полярного треугольника.Фактически именно благодаря научному вкладу ат-Туси тригонометрия стала самостоятельной наукой, отделившись от астрономии[14]. Историк науки М. М. Рожанская считает: «В полной мере самостоятельной наукой тригонометрию можно считать только тогда, когда она становится наукой о решении треугольников и тригонометрические трактаты содержат классификацию прямоугольных и косоугольных плоских и сферических треугольников, а также алгоритмы решения всех типовых задач, в частности решения косоугольных треугольников по трём сторонам и углам. Именно это содержится в… „Трактате о полном четырёхстороннике“ Насир ад-Дина ат-Туси»[17]. Ат-Туси принадлежит ряд сочинений, посвящённых учению о параллельных. Во-первых, эта теория рассматривается в соответствующем месте принадлежащего ат-Туси «Изложения Евклида». Одна из редакций этого сочинения была издана в 1594 году в латинском переводе в Риме. Доказательство V постулата из этого текста было ещё раз опубликовано Джоном Валлисом (1693). По работе Валлиса с этим доказательством был знаком Джироламо Саккери, подвергший это доказательство критике (1733). Кроме того, ат-Туси принадлежит специальный «Трактат, исцеляющий сомнение по поводу параллельных линий». Помимо теории параллельных линий самого ат-Туси, здесь даётся критика теорий параллельных его предшественников Ибн ал-Хайсама, Омара Хайяма и аль-Джаухари.
В своих математических сочинениях ат-Туси неоднократно применял кинематические представления. Для доказательства геометрических положений он систематически пользуется методом наложения (например, при доказательстве IV постулата о равенстве прямых углов, свойств диаметра круга и т. д.), указывая, впрочем, что совпадение геометрических величин при наложении является лишь достаточным признаком их равенства. Линию ат-Туси рассматривает как путь, проходимый движущейся точкой, а круг определяет с помощью вращения отрезка. Вслед за Архимедом он применяет движение при определении таких фигур, как шар и круговые цилиндр и конус[18].
Для сравнения прямых и кривых линий и поверхностей ат-Туси применяет ещё один вид движения — качение. «Прямую линию, — говорит он, — можно наложить на круговую или кривую линию, не отказываясь от её прямизны, то есть не изгибая её. Это получается движением круга по прямой линии, которая является касательной к нему, когда он катится по прямой до возвращения к начальному положению»[18].
Аналогичным образом с помощью качения на плоскости ат-Туси определяет поверхности цилиндра и конуса и специально останавливается на качении шара внутренним образом по шаровой поверхности другого радиуса. При этом ат-Туси исходил из представления, по которому прямая и кривая состоят из актуально бесконечно малых неделимых частей — точек, которые при качении налагаются друг на друга, и такое наложение происходит в течение всего процесса движения[19].
В «Сборнике по арифметике с помощью доски и пыли» (1265) ат-Туси подробно описал приём извлечения корней любой степени на примере . Ат-Туси приводит здесь таблицу биномиальных коэффициентов в форме треугольника, известного ныне как треугольник Паскаля.
Ат-Туси комментировал также труды Архимеда «Об измерении круга» и «О шаре и цилиндре».

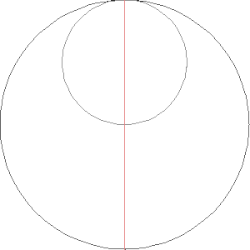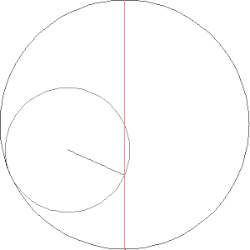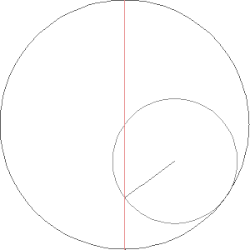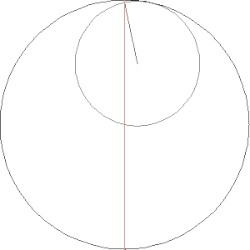
В механике научные достижения Насир ад-Дина ат-Туси относятся прежде всего к кинематике. Существенным вкладом ат-Туси в данный раздел механики стала так называемая лемма Туси: если даны два круга с радиусами R и 2R и малый круг катится без проскальзывания по большому, касаясь его с внутренней стороны, то произвольная точка M окружности малого круга совершает прямолинейное колебательное движение вдоль диаметра большого круга[20].
Доказывая эту лемму, ат-Туси представил движение малого круга как результат сложения двух круговых движений. С современной точки зрения, речь идёт о сложном движении абсолютно твёрдого тела: имеет место сложение двух вращений вокруг параллельных осей (причём угловая скорость относительного движения по модулю вдвое больше угловой скорости переносного движения и направлена в противоположную сторону); совокупность двух таких вращений образует так называемую пару Туси[комм. 2]. Если оба вращения являются равномерными, то точка M совершает гармоническое колебание[21].
Лемма ат-Туси впоследствии применялась такими учёными, как аш-Ширази, Ибн аш-Шатиром и др., а затем и Коперником.
Теоретические достижения ат-Туси имели для механики большое значение, позволяя преодолеть господствовавшее со времён Аристотеля противопоставление двух видов движений: свойственных небесным телам равномерных круговых движений и свойственного земным телам «местного» прямолинейного движения. Получив прямолинейное движение как результат сложения двух круговых, ат-Туси перебросил мост через эту пропасть и показал, что в движении небесных тел прямолинейное движение участвует равноправно с круговым[22]. В результате небесная и земная кинематика оказывались объединёнными в единую науку с законами, универсальными для всех изучаемых тел[23].
В 1259 ат-Туси основал крупнейшую в то время в мире Марагинскую обсерваторию близ Тебриза[14]. Когда ат-Туси поставил перед Хулагу вопрос о строительстве обсерватории, расходы на это показались тому чрезмерно большими. Тогда ат-Туси предложил Хулагу во время ночёвки его войска в горах спустить с горы медный таз. Таз, падая, произвел большой шум и панику среди войска, и ат-Туси сказал: «Мы знаем причину этого шума, а войска не знают; мы спокойны, а они волнуются; также если мы будем знать причины небесных явлений, мы будем спокойны на земле». Эти слова убедили Хулагу, и он отпустил на строительство обсерватории 20 тысяч динаров. Хулагу по просьбе ат-Туси распорядился всех учёных, которые попадали в руки его воинов, не убивать, а привозить в Марагу, туда же монголы свозили все попавшие в их руки рукописи и астрономические приборы.
Обсерватория была оснащена многочисленными инструментами новой конструкции, наибольшим из которых был стенной квадрант радиусом 6,5 м. В обсерватории имелись также армиллярные сферы и инструмент с двумя квадрантами для одновременного измерения горизонтальных координат двух светил. Сотрудниками обсерватории в Мараге были ас-Самарканди, аль-Казвини, аль-Магриби, аш-Ширази и многие другие известные учёные. Марагинская обсерватория оказала исключительное влияние на обсерватории многих стран Востока, в том числе на обсерваторию в Пекине.
Итогом 12-летних наблюдений марагинских астрономов с 1259 по 1271 год были «Ильханские таблицы» («Зидж Ильхани»). В этом зидже содержались таблицы для вычисления положения Солнца и планет, звёздный каталог, а также первые шестизначные таблицы синусов и тангенсов с интервалом 1'. На основании наблюдений звёзд ат-Туси очень точно определил величину предварения равноденствий (51,4').
Ат-Туси также считается основателем ещё одной обсерватории, большей известной как башня Радекан (Радкан), расположенной в одноимённой деревне в 80 км от Мешхеда. Точная дата строительства неизвестна. Предположительно, башня была возведена за несколько лет до Марагинской обсерватории[24][25].
Ат-Туси составил также изложение «Альмагеста» Клавдия Птолемея и ряд других астрономических трактатов: «Трактат Муинийа по астрономии», дополнение к нему, «Сливки познания астрономии небесных сфер», «Памятку по астрономии». В этом цикле трактатов ат-Туси строит свою схему кинематики небесных тел, отличную от птолемеевской.
Разработанная ат-Туси кинематическая модель движения Луны опирается на упоминавшуюся выше лемму Туси. В духе античной традиции он вводит для Луны систему равномерно вращающихся сфер; среди них выделены две такие («малая» и «большая»), что малый и большой круги леммы оказываются большими кругами данных сфер (то есть «малая» сфера катится внутри «большой»). При помощи этой модели Туси удалось объяснить установленное по данным наблюдений непостоянство угловой скорости центра эпицикла Луны при наблюдении из центра Мира; при этом он обошёлся без отказа от принципа равномерного кругового движения (в то время как птолемеева теория движения Луны, использующая гипотезу экванта, существенно отходила от данного принципа)[21].
Хотя лунная модель ат-Туси по точности совпадения с данными наблюдений не превосходила птолемееву (и даже в некотором смысле ей уступала), она оставила значительный след в истории небесной механики, став важным этапом в развитии нептолемеевских методов кинематико-геометрического моделирования[26].
Аналогичным образом ат-Туси поступал и при моделировании движения планет[27].
Ат-Туси принадлежат также «Трактат в двадцати главах о познании астролябии», «Трактат о синус-квадранте» и другие трактаты об астрономических инструментах.
Ат-Туси — автор целого ряда трактатов в других областях науки. Известны его трактаты физического содержания: «Обработка „Оптики“ Евклида», «О радуге», «О жаре и холоде». Он составил минералогическое сочинение, основанное на трудах ал-Бируни и других учёных. Ат-Туси написал ряд книг по медицине, в том числе и комментарий к «Канону» Ибн Сины. Серия его трактатов посвящена логике, философии и этике. Он написал также ряд богословских сочинений и трактат о финансах.

Именем Насир ад-Дина ат-Туси названы:
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.