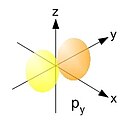
Orbital p

Orbital p – taki orbital, czyli falowa funkcja własna elektronu w polu oddziaływania jądra lub rdzenia atomowego, która odpowiada pobocznej liczbie kwantowej ${\displaystyle l=1.}$ Od wartości głównej liczby kwantowej ${\displaystyle (n)}$ zależy energia elektronu, a od wartości magnetycznej liczby kwantowej ${\displaystyle (m=0,\pm 1)}$ – funkcja rozkładu określająca „gęstość ładunku” (kwadrat modułu funkcji falowej) w różnych punktach otoczenia jądra. Orbitale ${\displaystyle p_{x},}$ ${\displaystyle p_{y},}$ ${\displaystyle p_{z}}$ mają formę wzajemnie prostopadłych „obrotowych ósemek”, łącznie wypełniających sferę wokół jądra (podobnie jak orbital s). Radialny rozkład gęstości cechują maksima (w liczbie ${\displaystyle n-1}$). Najwyższe z nich występuje w odległości od jądra zbliżonej do wartości promienia odpowiedniej orbity Bohra.

Orbitale (w wierszach: ${\displaystyle n}$ = 1, 2 i 3):
${\displaystyle s}$ – kolumna lewa
${\displaystyle p}$ – kolumna środkowa
${\displaystyle d}$ – po prawej

Równanie Schrödingera i orbitale

Równanie Schrödingera wiąże funkcję falową ${\displaystyle (\Psi )}$ z energią całkowitą ${\displaystyle (E).}$ Dla tzw. stanów stacjonarnych – takich, w których energia nie zmienia się w czasie – ma ogólną postać:

${\displaystyle {\hat {H}}\psi =E\psi ,}$

gdzie:

${\displaystyle {\hat {H}}}$ – operator Hamiltona.

Rozwiązania otrzymanego równania mają sens fizyczny dla ściśle określonych wartości energii całkowitej ${\displaystyle E_{n}}$ („wartości własne” operatora) i odpowiadających im „funkcji własnych” ${\displaystyle \Psi (r,\theta ,\phi )}$ – orbitali. W przypadku atomu wodoru lub „jonów (atomów) wodoropodobnych” całkowita energia układu jest wyrażana jako suma energii pędu elektronu wokół jądra i energii potencjalnej kulombowskich oddziaływań dwóch ładunków (zobacz równanie Schrödingera i orbitale). W czasie rozwiązywania równania stwierdza się (bez dodatkowych założeń), że ma ono sens tylko dla określonego zbioru liczb naturalnych – liczb kwantowych: głównej ${\displaystyle (n),}$ pobocznej ${\displaystyle (l)}$ i magnetycznej ${\displaystyle (m).}$ Jest to równoznaczne z wykazaniem, że energia elektronu, kwadrat momentu pędu i kota składowa momentu pędu są kwantowane. Każda z tak otrzymanych funkcji własnych ${\displaystyle \Psi _{nlm}(r,\Theta ,\phi )}$^[a] jest orbitalem. Orbitale przedstawia się jako iloczyny prostszych funkcji: ${\displaystyle R_{nl},}$ ${\displaystyle \theta _{lm}}$ i ${\displaystyle \Phi _{m}{:}}$

${\displaystyle \Psi _{nlm}(r\vartheta \phi )=R_{nl}(r)\cdot \Theta _{ml}(\vartheta )\cdot \Phi _{m}(\phi ).}$

Energia elektronu (wartość własna operatora) zależy od wartości ${\displaystyle n}$ ${\displaystyle (E_{n}),}$ a wartość funkcji własnej ${\displaystyle (\Psi _{nlm})}$ – od ${\displaystyle n,}$ ${\displaystyle l}$ i ${\displaystyle m.}$ Kwadrat bezwzględnej wartości modułu tej funkcji określa gęstość prawdopodobieństwa znalezienia elektronu w danym miejscu otoczenia jądra (zobacz: gęstość elektronowa).

W przypadku orbitali ${\displaystyle s}$ (${\displaystyle l=0;}$ symbole ${\displaystyle 1s,}$ ${\displaystyle 2s,}$ ${\displaystyle 3s,\dots }$) gęstość elektronowa nie zależy od parametrów ${\displaystyle \Theta }$ i ${\displaystyle \phi }$ (sferyczna „chmura elektronowa”). Rozkład radialny charakteryzuje się występowaniem ${\displaystyle n}$ maksimów. Dla każdego z tych orbitali gęstość jest największa w strefie tego maksimum, które leży najdalej od jądra.

Orbitale px, py, pz

Orbitale p_x, p_y, p_z

Gdy poboczna liczba kwantowa ${\displaystyle l\neq 0,}$ gęstość elektronowa w otoczeniu jądra lub rdzenia atomowego zależy od parametrów ${\displaystyle \Theta }$ i ${\displaystyle \phi ,}$ co sprawia, że chmura elektronowa nie jest sferyczna. Jej kształt zależy od pobocznej i magnetycznej liczby kwantowej (${\displaystyle l}$ i ${\displaystyle m}$).

Dla każdej wartości głównej liczby kwantowej ${\displaystyle (n)}$ poboczna liczba kwantowa może przyjmować wartości:

${\displaystyle l=0,1,2,\dots (n-1).}$

Dla każdej wartości pobocznej liczby ${\displaystyle l}$ liczba ${\displaystyle m}$ może przyjmować wartości, np.:

• gdy ${\displaystyle l}$ = 1 (orbital ${\displaystyle p}$), ${\displaystyle m}$ = 0, +1 lub -1 (inaczej: ${\displaystyle m}$ = 0, ±1; trzy możliwe wartości),
• gdy ${\displaystyle l}$ = 2 (orbital ${\displaystyle d}$), ${\displaystyle m}$ = 0, ±1, ±2 (5 wartości),
• gdy ${\displaystyle l}$ = 3 (orbital ${\displaystyle f}$), ${\displaystyle m}$ = 0, ±1, ±2, ±3 (7 wartości).

W przypadku orbitali ${\displaystyle p}$ dla każdej z trzech możliwych wartości liczby kwantowej ${\displaystyle m}$ otrzymuje się inną funkcję własną operatora energii, której odpowiada inny kształt chmury elektronowej. Kształt tej chmury jest wyjaśniany po zastąpieniu par funkcji ${\displaystyle \Phi _{-m}(\phi )}$ i ${\displaystyle \Phi _{+m}(\phi )}$ przez ich kombinacje liniowe.

Orbitale ${\displaystyle s,}$ ${\displaystyle p_{x},}$ ${\displaystyle p_{y}}$ i ${\displaystyle p_{z}}$^[b]
(przewiń galerię)

Rdzeń atomowy w centrum układu xyz

Orbital s

Orbital s i p_x

Orbital s i orbitale p_x p_y

Orbital s i orbitale p_x p_y p_z

Radialny rozkład gęstości prawdopodobieństwa
Porównanie orbitali ${\displaystyle s}$ i ${\displaystyle p}$
(przewiń galerię)

Orbital ${\displaystyle 2s;}$ dwa maksima (2 – 0)

Orbital ${\displaystyle 2p;}$ jedno maksimum (2 – 1)

Orbital ${\displaystyle 3s;}$ trzy maksima (3 – 0)

Orbital ${\displaystyle 3p;}$ dwa maksima (3 – 1)

W przypadku orbitalu ${\displaystyle p}$ można zamiast funkcji ${\displaystyle \Phi _{-1}(\phi )}$ i ${\displaystyle \Phi _{+1}(\phi ){:}}$

${\displaystyle \Phi _{+1}(\phi )={\frac {1}{\sqrt {2\pi }}}\exp(+i\phi ),}$

${\displaystyle \Phi _{-1}(\phi )={\frac {1}{\sqrt {2\pi }}}\exp(-i\phi )}$

zastosować funkcje ${\displaystyle \Phi _{1cos}(\phi )}$ i ${\displaystyle \Phi _{1sin}(\phi ){:}}$

${\displaystyle \Phi _{1sin}(\phi )={\frac {1}{\sqrt {1\pi }}}\sin(\phi ),}$

${\displaystyle \Phi _{1cos}(\phi )={\frac {1}{\sqrt {1\pi }}}\cos(\phi ).}$

Konsekwencją tej zamiany jest otrzymanie trzech ilorazów funkcji ${\displaystyle \theta _{lm}\Phi _{m},}$ dla m = 0, +1 i –1:

${\displaystyle \Theta _{1,0}(\vartheta )\Phi _{0}(\phi )={\frac {3}{\sqrt {4\pi }}}\cos(\vartheta )\equiv p_{z},}$

${\displaystyle \Theta _{1,+1}(\vartheta )\Phi _{1cos}(\phi )={\frac {3}{\sqrt {4\pi }}}\sin(\vartheta )\cos(\phi )\equiv p_{y},}$

${\displaystyle \Theta _{1,-1}(\vartheta )\Phi _{1sin}(\phi )={\frac {3}{\sqrt {4\pi }}}sin(\vartheta )\sin(\phi )\equiv p_{z}.}$

Bezwzględne wartości funkcji ${\displaystyle p_{z}}$ są największe wzdłuż osi ${\displaystyle z.}$ Wartości funkcji są dodatnie dla ${\displaystyle z>0}$ i ujemne dla ${\displaystyle z<0.}$ Na płaszczyźnie ${\displaystyle xy}$ funkcja ma wartość zero (płaszczyzna węzłowa).

Bezwzględne wartości funkcji ${\displaystyle p_{x}}$ są największe wzdłuż osi ${\displaystyle x.}$ Wartości funkcji są dodatnie dla x > 0 i ujemne dla x < 0. Płaszczyzną węzłową jest ${\displaystyle yz.}$

Bezwzględne wartości funkcji ${\displaystyle p_{y}}$ są największe wzdłuż osi ${\displaystyle y.}$ Wartości funkcji są dodatnie dla ${\displaystyle y>0}$ i ujemne dla ${\displaystyle y<0.}$ Płaszczyzną węzłową jest ${\displaystyle xz.}$

Określając prawdopodobieństwo znalezienia elektronu w określonych punktach otoczenia jądra, bierze się pod uwagę wartości kwadratu modułu funkcji falowej (zgodnie z interpretacją Maxa Borna). Graficznym obrazem chmur elektronowych ${\displaystyle p_{x},}$ ${\displaystyle p_{y},}$ ${\displaystyle p_{z}}$ są bryły określane jako „obrotowe ósemki” lub „hantle”, wewnątrz których prawdopodobieństwo znalezienia elektronu wynosi np. 90%. Zależność gęstości tego prawdopodobieństwa od odległości od centralnego ładunku określa funkcja ${\displaystyle R_{nl}(r).}$ Nie jest ona zależna od ${\displaystyle m,}$ a więc radialne funkcje rozmieszczenia na orbitalach ${\displaystyle p}$ mają kształt podobny do opisanego w odniesieniu do orbitalu s. Funkcje te cechuje występowanie maksimów w liczbie ${\displaystyle (n-l).}$ Oznacza to np. że w przypadku gdy:

• ${\displaystyle n=2}$ i ${\displaystyle l=1}$ (orbital 2p) występuje jedno maksimum gęstości chmury elektronowej,
• ${\displaystyle n=3}$ i ${\displaystyle l=1}$ (orbital 3p) – dwa maksima,
• ${\displaystyle n=5}$ i ${\displaystyle l=1}$ (orbital 5p) – cztery maksima.

W każdym przypadku najwyższym z maksimów jest to, dla którego ${\displaystyle r}$ przyjmuje największą wartość, jednocześnie w przybliżeniu odpowiadając promieniowi orbity Bohra.

Zobacz też

• hybrydyzacja (chemia)
• sprzężone wiązania wielokrotne
• wiązanie pi
• wiązanie sigma
• wiązanie wielokrotne

Uwagi

1. Oznaczenia: ${\displaystyle r,}$ ${\displaystyle \Theta ,}$ ${\displaystyle \phi }$ – współrzędne punktu w biegunowym układzie współrzędnych.
2. Trzy orbitale ${\displaystyle p}$ powinny wypełniać sferę, analogicznie jak orbital ${\displaystyle s}$ (przedstawiono formy zwężone, dla zachowania czytelności rysunku).

Bibliografia

Zobacz multimedia związane z tematem: Orbital p

• Heinz A. Staab: Wstęp do teoretycznej chemii organicznej. Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1966, s. 7–12.
• Przykłady zastosowań równania Schrödingera; Widma cząsteczkowe; Fotochemia. W: Stanisław Bursa: Chemia fizyczna. Warszawa: Państwowe Wydawnictwo Naukowe PWN, 1979, s. 46–61. ISBN 83-01-00152-6.
• Antoni Basiński, Adam Bielański, Kazimierz Gumiński i inni: Chemia fizyczna. Wyd. 3. Warszawa: Państwowe Wydawnictwo Naukowe, 1966, s. 86–110.

Encyklopedie internetowe (Orbital):

• Britannica: science/p-orbital