順序集合

順序集合（じゅんじょしゅうごう、英: ordered set）は集合の要素の間に順序が定義された集合。順序とは二項関係であって後述する反射律・推移律などを満たすものであり、数の大小関係などを一般化したものである。

全ての2要素が比較可能（順序が定義されている）ものを特に全順序集合（totally ordered set; toset）という。例えば実数における大小関係は全順序集合である。

また、全順序ではない順序集合の例としては、正の整数全体の集合に整除関係で順序を定めたものや、（2つ以上元を含む）集合の冪集合において、包含関係を順序と見なしたものがある。

後述するように、順序が満たすべき公理の種類により、前順序集合、半順序集合（partially ordered set; poset）、全順序集合がある。多く場合、半順序集合を指して「順序集合」と呼ぶことが多いが、分野によっては前順序集合や全順序集合を指す場合がある。

まず、二項関係について以下の用語を定める。

ここで $P$ は集合であり、「 $\leq$ 」を $P$ 上で定義された二項関係とする。

反射律： $P$ の任意の元 $a$ に対し、 $a \leq a$ が成り立つ。
推移律： $P$ の任意の元 $a$ , $b$ , $c$ に対し、 $a \leq b$ かつ $b \leq c$ ならば $a \leq c$ が成り立つ。
反対称律： $P$ の任意の元 $a, b$ に対し、 $a \leq b$ かつ $b \leq a$ ならば $a = b$ が成り立つ。
全順序律： $P$ の任意の元 $a, b$ に対し、 $a \leq b$ または $b \leq a$ が成り立つ。

また、「 $\leq$ 」が全順序律を満たさない場合（すなわち $a \leq b$ でも $b \leq a$ ないとき、 $a$ と $b$ は比較不能 (incomparable) であると言う。

前順序・半順序・全順序

$P$ を集合とし、 $\leq$ を $P$ 上で定義された二項関係とする。

$\leq$ が反射律と推移律を満たすとき、 $\leq$ を $P$ 上の前順序（英語版） (preorder) または擬順序 (quasiorder) という。
$\leq$ が前順序でありさらに反対称律を満たすとき、 $\leq$ を $P$ 上の半順序 (partial order) という。
$\leq$ が半順序でありさらに全順序律を満たすとき、 $\leq$ を $P$ 上の全順序 (total order) という。

$\leq$ が前順序であるとき $(P, \leq)$ を前順序集合という。同様に $\leq$ が半順序なら $(P, \leq)$ は半順序集合、全順序なら $(P, \leq)$ は全順序集合であるという。また集合 $P$ は $(P, \leq)$ の台集合 (underlying set) あるいは台 (support) と呼ばれる。紛らわしくなければ $\leq$ を省略し、 $P$ を（いずれかの意味で）順序集合という。

順序集合 $(P, \leq)$ に対し、 $\leq$ を台 $P$ 上の順序関係ともいう。

上では順序を記号 $\leq$ で表したが、必ずしもこの記号で表現する必要はない。実数の大小を表す記号 $\leq$ と区別するため、順序の記号として $\prec$ や $\ll$ を使うこともある。

全順序を線型順序ともいい、全順序集合を鎖と呼ぶこともある。また半順序集合の部分集合 $A$ で $A$ の任意の異なる2元が比較不能であるものを反鎖（英語版）という。半順序集合のことを部分順序集合と呼ぶこともある^[要出典]が部分順序集合は順序集合の部分集合に自然な順序を入れたものも指す。

半順序集合の元 $a$ が他の元 $b$ によって被覆される（英語版） ( $a <: b$ ) とは、 $a$ は $b$ よりも真に小さく、かつそれらの間に別の元が入ることはないことをいう。つまり $a<:b$ とは次の3つがすべて成り立つことである： $a\leq b,\quad a\neq b,\quad \neg [\exists \ c\ {\text{s.t.}}\ a<c<b].$

順序集合の例

実数全体の集合 $R$ およびその部分集合（例えば、自然数全体の集合 $N$ , 整数全体の集合 $Z$ , 有理数全体の集合 $Q$ ）は、通常の大小関係により全順序集合となる。しかし、複素数全体の集合 $C$ には複素数の乗法と"両立"する全順序は存在しない（順序体でない）。単に全順序を入れるだけであれば、直積集合 $R \times R$ に辞書式順序を定めることができる。
自然数全体の成す集合は整除関係を順序として半順序集合である。
集合の冪集合に対して、包含関係による順序を入れると半順序集合となる。これはもとの集合の元の個数が2個以上であれば全順序でない。例えば ${1, 2, 3}$ の冪集合

{\bigl \{}\emptyset ,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}{\bigr \}}

について、例えば

{1, 2}

と

{2, 3}

を考えれば、これらは比較不能であり（

{1, 2} \leq {2, 3}

でも

{2, 3} \leq {1, 2}

でもない）、全順序ではない。

線形空間の部分空間全体は包含関係で順序付けられた半順序集合である。
半順序集合 $P$ に対し、 $P$ の元の（自然数で添え字付けられた）列全体の成す集合は、列 $a = (a n) n \in N$ , $b = (b n) n \in N$ に対し、
$a\leq b\iff a_{n}\leq b_{n}\;(\forall n\in \mathbb {N} )$
と定めると半順序集合となる。
集合 $X$ と半順序集合 $P$ に対し、 $X$ から $P$ への写像全体の成す写像空間（英語版）は、2つの写像 $f, g$ に対して、 $f \leq g$ を $X$ の任意の元 $x$ に対して $f (x) \leq g (x)$ となることとして定義すると、半順序集合になる。
有向非巡回グラフの頂点集合は、到達不可能性によって順序付けられる。
半順序集合における順序関係の向きが $a < b > c < d \dots$ というように交互に入れ替わる列をフェンス（英語版）と呼ぶ。

上で述べた順序関係「 $\leq$ 」は直観的には左辺が右辺「よりも小さい、もしくは等しい」ことを意味しているが、逆に左辺が右辺「よりも大きい、もしくは等しい」順序関係や等しいことを許容しない順序関係を考えることもできる。

逆順序

「大きい、もしくは等しい」ことを意味する順序関係は「 $\leq$ 」の逆順序と呼ばれ、

a\geq b\iff b\leq a

により定義される。

狭義の順序

一方、等しいことを許容しない順序は狭義の（半）順序と呼ばれ、以下のように定義される：

a<b\iff (a\leq b\land a\neq b)

…(1)

狭義の逆順序「 $>$ 」も同様に定義される。

狭義の順序「 $<$ 」の対義語として、等しいことも許容する順序「 $\leq$ 」のことを広義の（半）順序（もしくは弱い意味 (weak) の（半）順序、反射的 (reflexive) な(半)順序）という。

(1) 式で定義された「 $<$ 」を「 $\leq$ 」の反射的簡約 (reflexive reduction) という。

「 $\leq$ 」が半順序であるとき、その反射的簡約「 $<$ 」は任意の $a, b, c \in P$ に対して以下を満たす：

非反射性： $\neg(a < a)$ ;
非対称性： $a < b$ ならば $\neg(b < a)$ ; （非反射性と推移性から従う）
推移性： $a < b$ かつ $b < c$ ならば $a < c$

以上では広義の順序を定義してから狭義の順序を定義したが、逆に上の三性質（非対称性は非反射性と推移性より得られるので条件としては不要）を満たすものを狭義の順序として定義し、広義の順序を

a\leq b\iff a<b\lor a=b

…(2)

により定義することもできる。この場合、(2) 式で定義された「 $\leq$ 」を「 $<$ 」の反射閉包（英語版）という。「 $<$ 」が前述の3条件を満たせば反射閉包「 $\leq$ 」が半順序であることを簡単に示すことができる。

双対順序集合

$(P, \leq)$ を順序集合とするとき、P 上の二項関係「 $\preccurlyeq$ 」を

a\preccurlyeq b\iff b\leq a

と定義する（すなわち「 $\preccurlyeq$ 」は「 $\leq$ 」の逆順序を順序と見なしたものである）。すると、「 $\preccurlyeq$ 」も $P$ 上の順序になっていることが容易に分かる。 $(P,\preccurlyeq )$ を $(P, \leq)$ の双対順序集合という。

双対順序集合はその定義 $(P,\preccurlyeq )$ よりもとの順序集合 $(P, \leq)$ とは"大小が逆転"している。したがって $(P, \leq)$ における上限、極大元、最大元（定義は後述）は $(P,\preccurlyeq )$ ではそれぞれ下限、極小元、最小元に対応している。

$P$ を有限集合とし、「 $<$ 」を $P$ 上の狭義の半順序とするとき、以下のようにして $P$ を自然に単純有向グラフと見なせる：

頂点：

P

の元

a \in P

から

b \in P

への辺がある

\Leftrightarrow a < b

であり、しかも

a < c < b

を満たす

c \in P

が存在しない

（すなわち

b

は

a

を被覆している）

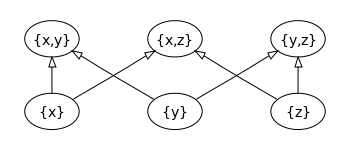
この有向グラフを図示したものをハッセ図という。

ハッセ図を用いると、順序関係に関する基本的な概念が図示できる。例えばこの図で ${x}$ と ${x, y, z}$ は比較可能だが、 ${x}$ と ${y}$ は比較不能である。また単集合の族 ${{x}, {y}, {z}}$ は反鎖である。さらに ${x}$ は ${x, z}$ によって被覆されるが、 ${x, y, z}$ には被覆されない。

なお、有限半順序集合から前述の方法で作ったグラフは閉路を持たない。逆に $(V, E)$ を閉路を持たない有限な単純有向グラフとすると、 $V$ 上に以下の順序を入れることで $V$ を半順序集合と見なせる：

a < b \Leftrightarrow a

から

b

への道がある

したがって有限半順序集合は閉路を持たない有限な単純有向グラフと自然に同一視できる。

$P$ を半順序集合とし、 $A$ をその部分集合とし、 $x$ を $P$ の元とする。このとき上界、上限、最大、極大の概念、およびこれらの双対概念である下界（かかい）、下限、最小、極小は以下のように定義される^[1]：

$x$ が $A$ の上界 (upper bound) であるとは、 $A$ の任意の元 $y$ に対して $y \leq x$ となること。
$x$ が $A$ の上限 (supremum) あるいは最小上界 (least upper bound) であるとは、 $x$ が $A$ の上界全体の集合の最小元となること。これは存在すれば一意的に決まり、 $sup A$ あるいは $lub A$ と表される。
$x$ が $A$ の最大元 (maximum element) であるとは、 $x$ は $A$ の元であり、かつ $x$ は $A$ の上界であること。これは存在すれば一意的に決まり、 $max A$ で表される。
$x$ が $A$ の極大元 (maximal element) であるとは、 $x$ は $A$ の元であり、かつ $y > x$ を満たす $y \in A$ が存在しないこと。

$x$ が $A$ の下界 (lower bound) であるとは、 $A$ の任意の元 $y$ に対して $y \geq x$ となること。
$x$ が $A$ の下限 (infimum) あるいは最大下界 (greatest lower bound) であるとは、 $x$ が $A$ の下界全体の集合の最大元となること。これは存在すれば一意的に決まり、 $inf A$ あるいは $glb A$ と表される。
$x$ が $A$ の最小元 (minimum element) であるとは、 $x$ は $A$ の元であり、かつ $x$ は $A$ の下界であること。これは存在すれば一意的に決まり、 $min A$ で表される。
$x$ が $A$ の極小元 (minimal element) であるとは、 $x$ は $A$ の元であり、かつ $y < x$ を満たす $y \in A$ が存在しないこと。

上界および上限の定義において、 $x$ が必ずしも $A$ の元であるとは限らない、ことには注意が必要である。左閉右開の半開区間 $[a,b)$ には最大元は存在しないが上界および上限は存在する（つまり、 $b$ ）。

極大元の概念と最大元の概念は以下の点で異なる。まず $x$ が $A$ の極大元であるとは、 $A$ の元は「 $x$ 以下である」か、もしくは「 $x$ とは大小が比較不能である」かのいずれかである事を意味する。一方 $x$ が $A$ の最大元であるとは $A$ の元は常に $x$ 以下である事を意味する（このとき $x$ は $A$ の任意の元と比較が可能である）。したがって最大元は必ず極大元であるが、極大元は必ずしも最大元であるとは限らない（下の具体例参照）。全順序集合においては必ず極大元は最大元に一致する。

さらに $A$ が $P$ の上方集合（resp. 下方集合）であるとは、任意の $a \in A$ と $x > a$ (resp. $x < a$ ) を満たす任意の $P$ の元に対し $x \in A$ となることをいう。

具体例

正整数全体の成す集合を整除関係で順序付けるとき、 $1$ は任意の正整数を割り切るという意味において $1$ は最小元である。しかしこの半順序集合には最大元は存在しない（任意の正整数の倍数としての $0$ を追加して考えたとするならば、それが最大元になる）。この半順序集合には極大元も存在しない。実際、任意の元 $g$ はそれとは異なる。例えば $2 g$ を割り切るから $g$ は極大ではありえない。この半順序集合から最小元である $1$ を除いて、順序はそのまま整除関係によって入れるならば、最小元は無くなるが、極小元として任意の素数をとることができる。この半順序に関して $60$ は部分集合 ${2, 3, 5, 10}$ の上界（上限ではない）を与えるが、 $1$ は除かれているので下界は持たない。他方、 $2$ の冪全体の成す部分集合に対して $2$ はその下界（これは下限でもある）を与えるが、上界は存在しない。

順序に関する写像の概念に以下のものがある：

定義

$S, T$ を順序集合とし、 $f : S \to T$ を写像とする。このとき

$f : S \to T$ が順序を保つ（英語版）(order-preserving)（同調 (isotone) とも）とは、

任意の

x, y \in S

に対して

x \leq y \Rightarrow f (x) \leq f (y)

$f : S \to T$ が順序を逆にする（order-reversing（英語版））とは、

任意の

x, y \in S

に対して

x \leq y \Rightarrow f (x) \geq f (y)

上の2つを合わせて単調 (monotone) 写像という。
$f$ が順序を反映する (order-reflecting) とは、

任意の

x, y \in S

に対して

f (x) \leq f (y) \Rightarrow x \leq y

$f$ が順序埋め込み（英語版）であるとは、

任意の

x, y \in S

に対して

x \leq y \Leftrightarrow f (x) \leq f (y)

$f$ が順序同型写像（英語版）であるとは、 $f$ が順序埋め込みな全単射であることをいう。

$f : S \to T$ が順序埋め込みであるとき、 $S$ は $f$ によって $T$ に（順序集合として）埋め込まれるという。また順序同型 $f : S \to T$ が存在するとき、 $S$ と $T$ は順序同型あるいは単に同型であるという。

性質

上で述べた概念は以下の性質を満たす：

順序を反映する写像は単射である。実際 $f (x) = f (y) \Rightarrow f (x) \leq f (y)$ かつ $f (x) \geq f (y) \Rightarrow x \leq y$ かつ $x \geq y \Rightarrow x = y$ である。
$f$ が順序埋め込みである必要十分条件は $f$ が順序を保存し、しかも順序を反映することである。また全単射 $f : S \to T$ とその逆関数 $f - 1 : T \to S$ が順序同型なら $f$ , $f - 1$ は順序同型である。
順序を保つ写像と順序を保つ写像の合成は順序を保つ。順序を反映する写像と順序を反映する写像の合成も順序を反映する。

具体例

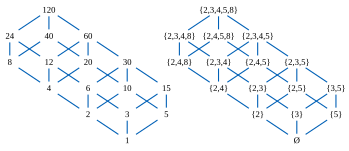自然数全体が整除関係に関して成す半順序集合から、その冪集合が包含関係に関して成す半順序集合への写像 $f : N \to P (N)$ を各自然数にその素因数全体の成す集合を対応させることにより定まる。これは順序を保つ集合である（すなわち、 $x$ が $y$ を割るならば $x$ の各素因数は $y$ の素因数にもなる）が単射ではない（例えば $12$ も $6$ もこの写像で ${2, 3}$ に写る）し、順序を反映もしない（例えば $12$ は $6$ を割らない）。少し設定を変えて、各自然数にその素冪因子の集合を対応させる写像 $g : N \to P (N)$ を考えれば、これは順序を保ち、かつ順序を反映するから、従って順序埋め込みになる。一方、これは順序同型ではない（実際、たとえば単集合 ${4}$ に移る数は無い）が終域を $g$ の値域 $g (N)$ に変更すれば順序同型にすることができる。このような冪集合の中への順序同型の構成は、より広汎な分配束（英語版）と呼ばれる半順序集合のクラスに対して一般化することができる（バーコフの表現定理（英語版）の項を参照）。

$P$ を順序集合とし、 $a, b$ を $P$ の元とするとき、閉区間 $[a, b]$ と開区間 $(a, b)$ を以下のように定義する：

[a,b]:=\{x\in P\mid a\leq x\leq b\}

(a,b):=\{x\in P\mid a<x<b\}

さらに $[a, b)$ および $(a, b]$ を以下のように定義し、半開区間と呼ぶ：

[a,b):=\{x\in P\mid a\leq x<b\}

(a,b]:=\{x\in P\mid a<x\leq b\}

文献によっては $(a, b)$ , $[a, b)$ , $(a, b]$ のことを $] a, b [$ , $[a, b [$ , $] a, b]$ と表す場合もある。

半順序集合が局所有限（英語版）であるとは、全ての区間が有限集合であることをいう。例えば、整数全体の成す集合は通常の大小関係による半順序に関して局所有限である（端点の無い無限区間のようなものは今考えていない）。

順序集合における区間の概念と、区間順序（英語版）として知られる特定の半順序の類いとを混同してはならない。

全順序集合の位相

順序位相

全順序集合 A に対し、無限半開区間

(-\infty ,b)=\{x\in A\mid x<b\}

(a,\infty )=\{x\in A\mid a<x\}

全体の集合を準開基とする位相を順序位相 (order topology) という^{[注 1]}。例えば、実数全体の集合 $\mathbb {R}$ を通常の大小関係 ≤ による全順序集合と見ると、その順序位相は通常の距離により定められる位相と同等になる。

全順序集合 A の部分集合 B には、B を全順序集合と見なした時の順序位相と A の順序位相から誘導される位相との2つの位相が入る。しかしこの2つの位相は一致するとは限らない。（B の順序位相における開集合は誘導位相でも開集合であるが逆は一般には成り立たない）。

例えば A を実数全体の集合とし、A の部分集合

B=\{x\mid 0<x<1\}\cup \{2\}

を考えると、A からB に誘導される位相では一元集合 ${2}$ は明らかに開集合であるが、B は順序集合としてみたときはそうではない。実際 B は（2を1に移す写像により） $C=\{x\mid 0<x\leq 1\}$ と順序同型だが、C の順序位相で ${1}$ は開集合ではないので B の順序位相で ${2}$ は開集合ではない。

上極限位相、下極限位相

単に「実数体上の位相」といった場合、前述の順序位相を指すがその他の位相を考えることも（主に反例として用いるために）できる。

実数体 $\mathbb {R}$ 上の上極限位相とは

(a,b]=\{x\in \mathbb {R} ~:~a<x\leq b\}

全体の集合を開基とする位相のことであり、同様に $\mathbb {R}$ 上の下極限位相（英語版）とは逆向きの半開区間

[a,b)=\{x\in \mathbb {R} ~:~a\leq x<b\}

全体の集合を開基とする位相のことである^{[注 2]}。

実数体に下極限位相を入れた空間はしばし $\mathbb {R} _{\ell }$ と書かれ、ゾルゲンフライ直線と呼ばれる。またゾルゲンフライ直線2つの直積 $\mathbb {R} _{\ell }\times \mathbb {R} _{\ell }$ はゾルゲンフライ平面（英語版）と呼ばれる。

overlapping interval topology

区間 [-1,1] 上の overlapping interval topology とは

[-1,a)

for

0<a

(b,1]

for

b<0

を準開基とする位相である。

半順序集合の位相

半順序空間

位相構造を持つ半順序集合P で以下の性質を満たすものを半順序空間（英語版）という：

a < b

を満たす任意の

a, b \in P

に対し、a の開近傍Uで上方集合であるものと b の開近傍V で下方集合であるものが存在することである。

（P の位相構造でこの性質を満たすものは1つとは限らないが、それらを全て半順序空間という。）なお、半順序空間と名前の似たposet topology（英語版）は別概念であるので注意が必要である。

定義より明らかに半順序空間は常にハウスドルフ性を満たす。

半順序空間では以下が成立する：

a i \to a, b i \to b

かつ任意の i に対して

a i \leq b i

ならば

a \leq b

である^[2]

位相構造を持つ半順序集合P が半順序空間である必要十分条件は以下を満たすことである：

半順序集合P 上の位相構造として、{(a, b) ∈ P × P | a ≤ b } が直積位相に関する閉部分集合になる。

2つ半順序空間の間の順序を保つ連続写像のことをdimapという。

上方位相、下方位相

順序集合 P 上の以下の2つの位相は同一である事が簡単に示せる。以下のいずれか一方（したがって両方）の条件を満たす位相を上方位相（英語版）という。

{x ∈ P | x ≤ a} for $a \in P$ を全て閉集合とする最弱の位相
任意の $a \in P$ に対し、一点集合 ${a}$ の閉包が{x ∈ P | x ≤ a} と一致する最弱の位相

下方位相も同様にして定義できる。

アレクサンドロフ空間

位相空間 P がアレクサンドロフ空間（英語版）であるとは、P 上の（有限または無限個の）任意の開集合の共通部分が必ず開集合になることである。

アレクサンドロフ空間は前順序集合と自然に1対1対応していることが知られている。実際任意の前順序集合 P に対し、

U が P の開集合 ⇔ U が P の上方集合

により P に位相を入れたものはアレクサンドロフ空間になる。（この位相を P のアレクサンドロフ位相という。）

逆に任意のアレクサンドロフ空間 P に対し P 上の「specialization preorder（英語版）」を前順序とすることで P を前順序集合と見なすことができる。

ここで位相空間 P のspecialization preorderとは

x\leq y\iff {\overline {\{x\}}}\subset {\overline {\{y\}}}

で定義される前順序のことである。上式で ${\overline {\{x\}}}$ は一元集合 ${x}$ の閉包である。（なお、P がT₀空間であればspecialization preorder は半順序であることが知られている。）

以上の対応関係により、集合P におけるアレクサンドロフ空間としての構造とP 上の前順序は1対1対応する。

specialization preorderはアレクサンドロフ空間でなくとも定義可能であるが、アレクサンドロフ空間でない位相空間上ではspecialization preorderに対して上方集合でない開集合も存在する。（なおこの場合でも開集合は常に上方集合である）。したがって前述したような、上方集合を開集合とする位相を考えても元の位相は復元できない。

実数体における例

実数体（に通常の順序をいれたもの）を前順序集合と見なすことで実数体にアレクサンドロフ位相を入れることができる。アレクサンドロフ位相における実数体上の開集合（すなわち上方集合）は以下のもののいずれかになる：

$(a,\infty )$ for some a
$[a,\infty )$ for some a
空集合 $\emptyset$ 、全体集合 $\mathbb {R}$

スコット位相

上で述べたようにアレクサンドロフ位相は $[a,\infty )$ のような「下に閉じた」集合すらも開集合と見なしてしまう。アレクサンドロフ位相からこのような不自然さを取り除いたのがスコット位相である。順序集合 P 上のスコット位相 (Scott topology) とは、以下の2条件を満たす P の部分集合 O 全体の集合を開集合族とする位相である：

O ⊂ P は上方集合である
P の有向部分集合 A で（A を自然に有向点族と見なしたときの）A の極限がO に入っていれば、A の点でO に含まれるものが存在する

後者の条件は内点概念の点列による特徴づけ（O の内点x に収束する点列はO と共通部分を持つ）に類似しており、この条件が「下に閉じた」集合を排除する。

よって実数体にスコット位相を入れた際、実数体上の開集合は以下のもののいずれかになる：

$(a,\infty )$ for some a
空集合 $\emptyset$ 、全体集合 $\mathbb {R}$

スコット位相を入れた順序集合をスコット空間といい、スコット空間からスコット空間への連続写像をスコット連続 (Scott continuity) という。順序集合 P から順序集合Q への写像 f がスコット連続である必要十分条件は以下の性質が成り立つことであることが知られている：

P の任意の有向部分集合A に対し、A がP 内の上限を持てばf (A )もQ 内の上限を持ち、sup f (A) = f (sup A ) が成立する。

スコット連続な関数は順序を保つ。実際、x ≥ y ⇒ sup{x , y } = x であるので、上述した条件より $sup{f (x), f (y)$ }が存在し、しかも sup{f (x ), f (y )} = f (sup{x , y }) = f (x ) となる。これは $f (x) \geq f (y)$ を意味する。

なお、スコット位相と下方位相のいずれよりも強い位相構造の中で最弱のものをローソン位相（英語版）という。

ストーン双対性

位相空間の開集合全体の集合は包含関係により順序集合と見なせる。位相空間が「sober性」という弱い性質を満たす時はこの順序構造のみで位相空間の構造が特徴づけられることが知られている（ストーンの双対性定理）。したがってsober性を満たす空間に話を限定すれば、点集合論に頼らなくても順序構造のみで位相空間論を展開できる（ポイントレス位相空間論）。

2つの半順序集合（の台集合）の直積集合上の半順序としては次の三種類がある。

辞書式順序： $(a,b)\leq (c,d)\iff a<c\lor (a=c\land b\leq d)$
積順序： $(a,b)\leq (c,d)\iff a\leq c\land b\leq d$
$(a,b)\leq (c,d)\iff (a<c\land b<d)\lor (a=c\land b=d)$

最後の順序は対応する狭義全順序の直積の反射閉包である。これらの三種類の半順序は、いずれも3個以上の半順序集合の直積に対しても同様に定義される。

体上の順序線型空間に対してこれらの構成を適用すれば、結果として得られる順序集合はいずれも再び順序線型空間となる。

$N \times N$ 上の直積狭義順序の反射閉包
$N \times N$ 上の積順序
$N \times N$ 上の辞書式順序

任意の半順序集合（および前順序集合）は、任意の射集合が高々一つの元からなる圏と見なすことができる。具体的には、射の集合を $x \leq y$ ならば $hom(x, y) = {(x, y)}$ （それ以外の場合は空集合）とし、 $(y, z)\circ(x, y) = (x, z)$ と定義する。2つの半順序集合が圏として同値となるのは、それらが順序集合として同型であるときであり、かつその時に限る。半順序集合に最小元が存在すればそれは始対象であり、最大元が存在すればそれは終対象となる。また、任意の前順序集合はある半順序集合に圏同値であり、半順序集合の任意の部分圏は同型射について閉じて（英語版）いる。

半順序集合からの函手、すなわち半順序圏で添字付けられた図式は、可換図式である。

（半順序関係の総数） $n$ 個の元からなる集合上の半順序の総数（狭義半順序の総数も同じ）は $1, 1, 3, 19, 219, 4231, \dots$ （オンライン整数列大辞典の数列 A001035）。同型を除いた総数は $1, 1, 2, 5, 16, 63, 318, \dots$ （オンライン整数列大辞典の数列 A000112）。
（線型順序拡大）半順序集合 $P$ の全順序集合への埋め込みを線型順序拡大（英語版） (linear extension) という。任意の半順序は全順序に拡張することができる（順序拡大原理（英語版）^[3]）。計算機科学において（有向非循環グラフの到達可能性（英語版）順序として表現される）半順序の線型拡張を求めるアルゴリズムは位相ソート (topological sorting) と呼ばれる。

反マトロイド（英語版）: 半順序集合よりも一般の順序付けの族を許すような、集合上の順序付けの一般化
因果集合
比較可能グラフ（英語版）
有向集合
次数付き順序集合（英語版）
半束
束 (束論)
順序群
準順序（英語版） (semiorder)
直並列半順序（英語版）
狭義弱順序（英語版）: "a < b または b < a の何れかが成り立つ" という関係が推移的となるような狭義半順序 "<"
完備半順序 (cpo)
ツォルンの補題
コンパクト要素

[脚注の使い方]

注釈

[注 1]
原理的には半順序集合であっても同様の概念を定義できるが、本稿の英語版をはじめ、筆者^[誰?]が調べた範囲^{[要文献特定詳細情報]}では全順序集合に対してのみ order topology を定義しているため、ここでは全順序のみに話を限定した。
[注 2]
実数体でなくとも上極限位相と下極限位相を考えることができるが、これも実数体以外に対してこれらの位相を定義した文献が見つけられなかったので、ここでは実数体のみを対象にした。

出典

[1]
花木章秀 (2021年1月22日). “集合論信州大学理学部数学科講義ノート 2020 年度後期 (2021/01/22)”. 2022年3月17日閲覧。
[2]
Ward, L. E. Jr (1954). “Partially Ordered Topological Spaces”. Proceedings of the American Mathematical Society 5 (1): 144-161. doi:10.1090/S0002-9939-1954-0063016-5.
[3]
Jech, Thomas (2008) [originally published in 1973]. The Axiom of Choice. Dover Publications. ISBN 0-486-46624-8

松坂和夫『集合・位相入門』岩波書店、1968年6月10日。ISBN 4-00-005424-4。
斎藤正彦『数学の基礎　集合・数・位相』東京大学出版会〈基礎数学14〉、2002年8月1日。ISBN 978-4-13-062909-6。
Deshpande, Jayant V. (1968). “On Continuity of a Partial Order”. Proceedings of the American Mathematical Society 19 (2): 383-386. doi:10.1090/S0002-9939-1968-0236071-7.
Schröder, Bernd S. W. (2003). Ordered Sets: An Introduction. Birkhäuser, Boston
Stanley, Richard P.. Enumerative Combinatorics 1. Cambridge Studies in Advanced Mathematics. 49. Cambridge University Press. ISBN 0-521-66351-2

オンライン整数列大辞典の数列 A001035: Number of posets with n labeled elements in the OEIS
オンライン整数列大辞典の数列 A000112: Number of posets with n unlabeled elements in the OEIS

[2] [注 1]
原理的には半順序集合であっても同様の概念を定義できるが、本稿の英語版をはじめ、筆者^[誰?]が調べた範囲^{[要文献特定詳細情報]}では全順序集合に対してのみ order topology を定義しているため、ここでは全順序のみに話を限定した。

[3] [注 2]
実数体でなくとも上極限位相と下極限位相を考えることができるが、これも実数体以外に対してこれらの位相を定義した文献が見つけられなかったので、ここでは実数体のみを対象にした。

[1] [1]
花木章秀 (2021年1月22日). “集合論信州大学理学部数学科講義ノート 2020 年度後期 (2021/01/22)”. 2022年3月17日閲覧。

[ward-1954-4] [2]
Ward, L. E. Jr (1954). “Partially Ordered Topological Spaces”. Proceedings of the American Mathematical Society 5 (1): 144-161. doi:10.1090/S0002-9939-1954-0063016-5.

[5] [3]
Jech, Thomas (2008) [originally published in 1973]. The Axiom of Choice. Dover Publications. ISBN 0-486-46624-8

[1]

[注 1]

[注 2]

[2]

[3]

前順序・半順序・全順序

順序集合の例

逆順序

狭義の順序

双対順序集合

具体例

定義

性質

具体例

全順序集合の位相

順序位相

上極限位相、下極限位相

overlapping interval topology

半順序集合の位相

半順序空間

上方位相、下方位相

アレクサンドロフ空間

実数体における例

スコット位相

ストーン双対性

注釈

出典

前順序・半順序・全順序

順序集合の例

逆順序

狭義の順序

双対順序集合

具体例

定義

性質

具体例

全順序集合の位相

順序位相

上極限位相、下極限位相

overlapping interval topology

半順序集合の位相

半順序空間

上方位相、下方位相

アレクサンドロフ空間

実数体における例

スコット位相

ストーン双対性

注釈

出典

定義

逆順序、狭義の順序、双対順序

ハッセ図

上界、最大、極大、上限、上方集合

写像と順序

区間

順序構造と位相構造

直積集合上の順序

圏としての順序集合

その他

関連項目

脚注

参考文献

外部リンク