Persegi panjang

Dalam geometri Euklides, persegi panjang adalah poligon dengan empat sudut siku-siku. Bangun datar dua dimensi ini juga dapat didefinisikan sebagai jajar genjang yang memiliki sudut siku-siku; atau secara mendetail sebagai bangun datar yang dibentuk oleh dua pasang sisi dengan masing-masingnya memiliki panjang yang sama, terletak sejajar dengan masing-masing pasangannya, dan saling tegak lurus dengan pasangan yang lain sehingga membentuk empat sudut yang semuanya siku-siku.

Persegi panjang
Persegi panjang
Sisi dan titik pojok	4
Simbol Schläfli	{ } × { }
Diagram Coxeter–Dynkin
Grup simetri	Dihedral (D2), [2], (*22), order 4
Sifat	konveks, isogonal, siklik Sudut dan sisi yang saling berhadapan bersifat saling kongruen

Persegi panjang dengan titik-titik sudut ABCD dinotasikan sebagai  ABCD. Lebih lanjut, sisi (rusuk) terpanjang dari bangun ini disebut dengan panjang, sedangkan sisi yang lebih pendek disebut dengan lebar. Persegi panjang dengan empat sisi memiliki panjang yang sama disebut dengan persegi.

Persegi panjang banyak terlibat dalam masalah teselasi (pengubinan), seperti pengubinan bidang oleh persegi-persegi panjang, atau pengubinan persegi panjang oleh poligon-poligon.

Definisi

Sebangun poligon konveks disebut persegi panjang jika dan hanya jika bangun tersebut merupakan salah satu dari beberapa bentuk berikut:^[1][2]

• jajar genjang dengan setidaknya satu sudut siku-siku,
• jajar genjang dengan kedua panjang diagonalnya sama besar,
• jajar genjang ${\displaystyle ABCD}$ dengan segitiga ${\displaystyle ABD}$ dan ${\displaystyle DCA}$ saling kongruen,
• poligon dengan empat sudut yang semuanya siku-siku,
• poligon dengan kedua diagonalnya saling berpotongan dan memiliki panjang yang sama,^[3]
• poligon konveks dengan sisi-sisi berurutan ${\displaystyle a,}$ ${\displaystyle b,}$ ${\displaystyle c,}$ dan ${\displaystyle d,}$ dan luas ${\displaystyle {\tfrac {1}{4}}(a+c)(b+d)}$.^[4]:fn.1
• poligon konveks dengan sisi-sisi berurutan ${\displaystyle a,}$ ${\displaystyle b,}$ ${\displaystyle c,}$ dan ${\displaystyle d,}$ dan luas ${\displaystyle {\tfrac {1}{2}}{\sqrt {(a^{2}+c^{2})(b^{2}+d^{2})}}.}$^[4]

Penggolongan tradisional

Persegi panjang adalah kasus khusus dari jajar genjang dan trapesium. Persegi adalah kasus khusu dari persegi panjang.

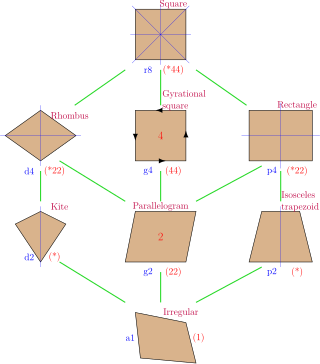
Persegi panjang adalah kasus khusus dari bangun jajar genjang, yang setiap pasangan sisi bersebelahannya saling tegak lurus. Jajar genjang selanjutnya adalah kasus khusus dari trapesium, yang sisi-sisi saling berhadapannya sejajar dan memiliki panjang yang sama. Trapesium adalah poligon konveks yang memiliki setidaknya sepasang sisi yang saling berhadapan. Poligon konveks adalah poligon yang:

• Sederhana: tidak ada sisi yang berpotongan dengan sisi(-sisi) lain dari poligon.
• Berbentuk bintang (star-shaped): Ada titik di dalam poligon yang dapat 'melihat' semua sisi poligon (tidak tertutup oleh suatu bagian dari poligon tersebut).

Sifat

Simetri

Persegi panjang memiliki dua garis simetri lipat dan dua garis simetri putar 180°. Persegi panjang bersifat siklik; artinya semua titik sudut bangun ini terletak pada suatu lingkaran.^[5] Lebih lanjut, persegi panjang juga bersifat sama-sudut (equiangular), dengan semua sudutnya berukuran 90 derajat. Bangun ini bersifat isogonal (vertex-transitive): semua sudut berada di orbit simetri yang sama.

Dualitas persegi panjang dan belah ketupat

Poligon dual dari persegi panjang adalah belah ketupat, sebagaimana terlihat pada tabel berikut.^[6]

Persegi panjang	Belah ketupat
Semua sudut sama besarnya.	Semua sisi sama besarnya.
Sisi yang saling berhadapan sama besarnya.	Sudut yang saling berhadapan sama besarnya.
Titik pusatnya berjarak sama dari semua titik sudutnya, sehingga memiliki lingkaran luar.	Titik pusatnya berjarak sama dari semua sisinya, sehingga memiliki lingkaran dalam.
Kedua garis simetri memotong dua sisi yang saling berhadapan.	Kedua garis simetri memotong dua sudut yang saling berhadapan.
Perpotongan kedua diagonal sama besar dalam panjangnya.	Perpotongan kedua diagonal sama besar dalam sudutnya.

Lain-lain

Dua persegi panjang, dengan yang satu tidak bisa diletakkan di dalam yang lainnya, dikatakan tidak dapat dibandingkan.

Rumus

Luas persegi panjang adalah hasil kali dari panjang dan lebarnya.

Jika persegi panjang memiliki length ${\displaystyle p}$ dan lebar ${\displaystyle l}$, maka:^[7]

• luasnya adalah ${\displaystyle L=p\cdot l}$ ;
• kelilingnya adalah ${\displaystyle K=2\cdot (p+l)}$ ;
• masing-masing diagonal memiliki panjang ${\textstyle d={\sqrt {p^{2}+l^{2}}}}$ ;
• dan jika ${\displaystyle p=l\,}$, persegi panjang tersebut adalah sebangun persegi.

Teorema

Berdasarkan teorema bendera Inggris, persegi-persegi berwarna merah memiliki total luas yang sama dengan persegi-persegi berwarna biru.

Teorema isoperimetrik untuk persegi panjang menyatakan bahwa di antara semua persegi panjang dengan keliling yang sama, persegi (yakni persegi panjang dengan semua panjang sisinya sama) memiliki luas terbesar.

Teorema bendera Inggris menyatakan bahwa untuk bangun persegi panjang dengan sudut A, B, C, dan D, dan sebarang titik P di dalam bangun tersebut, berlaku hubungan:^[8]$${\displaystyle \displaystyle (AP)^{2}+(CP)^{2}=(BP)^{2}+(DP)^{2}.}$$

Persegi panjang lainnya

Persegi panjang pelana memiliki 4 sudut nonplanar, yang diambil secara berseling dari sudut-sudut balok. Bangun ini memiliki permukaan minimal unik yang didefinisikan sebagai kombinasi linear dari keempat titik sudut, menghasilkan permukaan pelana. Gambar pada contoh ini memperlihatkan keempat sisi persegi panjang, dan dua diagonal berwarna hijau.

Dalam geometri bola, persegi panjang sferis adalah bangun yang dibentuk dari empat busur lingkaran besar yang berpotongan dengan besar sudut yang sama. Busur-busur yang saling berhadapan memiliki panjang yang sama, dan semua sudut perpotongan lebih besar dari 90°. Dari sudut pandang geometri eliptik, permukaan bola di geometri Euklides merupakan suatu permukaan non-Euklides. Geometri bola adalah bentuk geometri eliptik yang paling sederhana.

Dalam geometri eliptik, persegi panjang eliptik adalah bangun pada permukaan eliptik yang keempat sisinya adalah busur eliptik da n berpotongan pada suatu sudut yang lebih besar dari 90°. Busur-busur yang saling berhadapan memiliki panjang yang sama.

Dalam geometri hiperbolik, persegi panjang hiperbolik adalah bangun pada permukaan hiperbolik yang keempat sisinya adalah busur hiperbolik dan berpotongan pada suatu sudut yang lebih kecil dari 90°. Busur-busur yang saling berhadapan memiliki panjang yang sama.

Pengubinan

Persegi panjang digunakan dalam banyak pola teselasi periodik; beberapa contohnya dalam penyusunan bata sebagai berikut:

Unicode

Kode-kode Unicode berikut menyatakan persegi panjang:

• U+25AC ▬ BLACK RECTANGLE
• U+25AD ▭ WHITE RECTANGLE
• U+25AE ▮ BLACK VERTICAL RECTANGLE
• U+25AF ▯ WHITE VERTICAL RECTANGLE

Lihat juga

• Persegi

Referensi

1. Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition", Information Age Publishing, 2008, pp. 34–36 ISBN 1-59311-695-0.
2. Owen Byer; Felix Lazebnik; Deirdre L. Smeltzer (19 August 2010). Methods for Euclidean Geometry. MAA. hlm. 53–. ISBN 978-0-88385-763-2. Diakses tanggal 2011-11-13.
3. Gerard Venema, "Exploring Advanced Euclidean Geometry with GeoGebra", MAA, 2013, p. 56.
4. Josefsson Martin (2013). "Five Proofs of an Area Characterization of Rectangles" (PDF). Forum Geometricorum. 13: 17–21.
5. Dengan kata lain, dapat dibuat suatu lingkaran yang melewati semua titik sudut persegi panjang.
6. de Villiers, Michael, "Generalizing Van Aubel Using Duality", Mathematics Magazine 73 (4), Oct. 2000, pp. 303–307.
7. "Rectangle". Math Is Fun. Diakses tanggal 2024-03-22.
8. Hall, Leon M.; Robert P. Roe (1998). "An Unexpected Maximum in a Family of Rectangles" (PDF). Mathematics Magazine. 71 (4): 285–291. doi:10.1080/0025570X.1998.11996653. JSTOR 2690700. Parameter |name-list-style= yang tidak diketahui akan diabaikan (bantuan)