Symétrie (transformation géométrique)
transformation géométrique involutive qui conserve le parallélisme De Wikipédia, l'encyclopédie libre
Une symétrie géométrique est une transformation géométrique involutive[1] qui conserve le parallélisme[2]. Parmi les symétries courantes, on peut citer la réflexion (ou symétrie orthogonale) et la symétrie centrale.
Une symétrie géométrique est un cas particulier de symétrie. Il existe plusieurs sortes de symétries dans le plan ou dans l’espace.
Remarque : Le terme de symétrie possède aussi un autre sens en mathématiques. Dans l'expression groupe de symétrie, une symétrie désigne une isométrie quelconque. Ce terme désigne soit une translation, soit un automorphisme orthogonal, soit la composée des deux.
Symétrie dans le plan
Résumé
Contexte
Symétrie centrale (par rapport à un point)
Présentation
La symétrie de centre O est la transformation qui, à tout point M, associe le point M' tel que O soit le milieu de [MM'].
Construction : Tracez la droite (d) passant par A et O. Prolongez la au-delà de O. Avec un compas pointé en O et un écartement égal à OA, recoupez (d) en A'.
Le seul point invariant de cette symétrie est le point O.
Une symétrie de centre O est aussi une rotation d’angle plat et une homothétie de centre O et de rapport -1
Centre de symétrie
Une figure possède un centre de symétrie C si elle est invariante par la symétrie de centre C.

Exemples de centre de symétrie :
- Les lettres N, S et Z possèdent un centre de symétrie.
- Un parallélogramme possède pour centre de symétrie le point d’intersection de ses diagonales. Cette propriété est caractéristique des parallélogrammes : un quadrilatère ABCD possédant cette propriété est nécessairement un parallélogramme.
- L’hexagone est un polygone qui admet l’intersection de ses diagonales comme centre de symétrie.
- Le cercle admet son centre comme centre de symétrie.
- En analyse, une courbe d’équation y = f(x) possède un centre de symétrie C(a ; b) si et seulement si, pour tout réel h tel que a + h appartienne au domaine de définition de f, on a
- a - h appartient au domaine de définition
- f(a + h) + f(a - h) = 2b
- Lorsque le centre de symétrie est à l’origine du repère, la fonction est dite impaire. Dans ce cas l'expression précédente se simplifie en : f(- h) = - f(h).
Groupe des symétries centrales-translations
La composée de deux symétries de centres O et O', sO' o sO est une translation de vecteur

Cette propriété permet de définir un premier groupe de transformations du plan : celui des symétries centrales-translations. En effet, en composant deux symétries centrales ou translations, on obtient une symétrie centrale ou une translation. Et, pour obtenir l’application identique, il suffit de composer une translation de vecteur u par la translation de vecteur -u, ou de composer une symétrie centrale par elle-même.
La symétrie centrale conserve les distances et les angles orientés. C’est donc une isométrie positive ou déplacement. Le groupe défini précédemment est donc un sous-groupe du groupe des déplacements.
Symétrie axiale ou orthogonale par rapport à une droite
Présentation
On les appelle aussi des réflexions d’axe (d). La réflexion d’axe (d) est la transformation du plan qui laisse tous les points de (d) invariants et qui, à tout point M non situé sur (d), associe le point M' tel que (d) soit la médiatrice de [MM']. Comme il existe deux définitions équivalentes de la médiatrice, on connaît ainsi deux constructions équivalentes du point M'.
Construction
Données : l'axe de symétrie (d), le point A'.
Objectif : construire A' symétrique de A par la symétrie orthogonale d'axe (d).
- Première méthode :
- Tracez la droite perpendiculaire à (d) passant par A. Cette droite coupe l'axe en un point H.
- Tracez le cercle de centre H et de rayon HA. Ce cercle coupe (AH) en 2 points : A et A'.
- Deuxième méthode :
- Pour construire le point A' nous allons utiliser la propriété suivante :Tout point d'une médiatrice d’un segment est équidistant des extrémités de ce segment.
- Nous choisissons deux points quelconques c1 et c2 de (d) et nous allons déterminer l'unique point A' différent de A tel que c1A=c1A' et c2A=c2A'.
- Ainsi nous sommes certains que (c1c2), c’est-à-dire d, est la médiatrice de [AA'].
- Choisissez c1 et c2 sur (d).
- Tracez le cercle de centre c1 et de rayon c1A.
- Tracez le cercle de centre c2 et de rayon c2A.
- Les deux cercles se coupent en A et en A'.
- Sur cette figure, les points A" et C" ont été fait avec la première méthode et le point B' avec la seconde.
- Cette deuxième méthode est la méthode demandant le moins de construction euclidienne élémentaire (directement issue des axiomes de la géométrie euclidienne, c'est-à-dire droite passant par 2 point et cercle de rayon et centre donné).
- Elle ne demande que 2 cercles afin de trouver le symétrique alors que la première demande la perpendiculaire passant par un point donné qui n'est pas une construction euclidienne élémentaire. La perpendiculaire passant par un point donné demande au minimum 3 constructions euclidienne élémentaire.
Axe de symétrie
Une figure possède un axe de symétrie (d) si et seulement si elle est invariante par la réflexion d’axe (d)
Exemples de figures usuelles :
- Les lettres A, B, C, c, D, E, K, l, M, T, U, V, v, W, w possèdent généralement un axe de symétrie dans nombre de polices de caractères simples (non cursives et non italiques).
- Le cercle possède une infinité d’axes de symétrie : tous ses diamètres. Ce peut être parfois le cas des lettres O et o élargies (non cursives et non italiques).
- Un angle quelconque a toujours un axe de symétrie : sa bissectrice. Ce peut être parfois le cas de la lettre L élargie (non cursives et non italiques).
- Un segment quelconque a toujours un axe de symétrie : sa médiatrice. Ce peut être parfois le cas de la lettre I (non cursives et non italiques).
- Le triangle isocèle possède un axe de symétrie : sa bissectrice principale[3]. C’est généralement le cas de la lettre grecque delta majuscule Δ (non cursive et non italique).
- Le triangle équilatéral possède 3 axes de symétrie : ses 3 bissectrices.
- Le losange en possède 2 : ses 2 diagonales.
- Le rectangle en possède 2 : ses 2 médianes.
- Le carré en possède 4 : ses 2 diagonales (puisque c’est aussi un losange) et ses 2 médianes (puisque c’est aussi un rectangle).
- En analyse,
- une courbe d’équation y = f(x) possède un axe de symétrie d’équation x = a si et seulement si, pour tout h tel que (a + h) appartient au domaine de définition de f, on a :
- (a − h) appartient au domaine de définition, et
- f(a + h) = f(a − h) ;
- lorsque l’axe de symétrie est l’axe (Oy), c’est-à-dire ici l’axe d’équation x = 0 (donc avec a = 0), la fonction est dite paire : f(h) = f(−h)
- une courbe d’équation y = f(x) possède un axe de symétrie d’équation x = a si et seulement si, pour tout h tel que (a + h) appartient au domaine de définition de f, on a :
Une figure possédant deux axes de symétrie perpendiculaires a pour centre de symétrie le point d’intersection des deux droites. Par exemple, les lettres H, I, O, X dans des polices de caractère simples (non cursives et non italiques) possèdent souvent deux axes de symétrie perpendiculaires, donc aussi un centre de symétrie, de même le rectangle, le losange et le carré.
Réflexion et groupe des isométries
La réflexion conserve les distances et les angles. C’est donc une isométrie. Mais elle ne conserve pas l’orientation (voir chiralité). On dit que c’est un antidéplacement.
|
La composée de deux réflexions d’axes parallèles est une translation, de distance égale à deux fois la distance entre ces axes. Dans l’image ci-contre, les propriétés vectorielles des milieux permettent de dire que |
 |
|
La composée de deux réflexions d’axes sécants est une rotation, d’angle égal au double de l’angle formé entre les deux axes. Dans l’image ci-contre, les propriétés sur les bissectrices permettent de dire que |
 |
On remarque alors que l’ensemble des réflexions génère tout l’ensemble des isométries.
Symétrie oblique
La symétrie par rapport à une droite (d) suivant une direction (d') (non parallèle à (d)) est la transformation qui laisse tous les points de (d) invariants et qui, à tout point M non situé sur (d) associe le point M' tel que la droite (MM') soit parallèle à (d') et le milieu de [MM'] soit sur (d)
Cette symétrie est bien involutive : le symétrique de M’ est bien M. Elle offre moins d’intérêt que ses cousines car elle ne conserve pas les distances: elle déforme les figures. Cependant, elle conserve les barycentres et fait donc partie des transformations affines.
Symétrie dans l’espace
Résumé
Contexte
Symétrie centrale
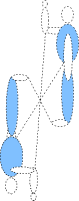
On retrouve la même définition et les mêmes propriétés que pour la symétrie centrale dans le plan, à ceci près qu’une symétrie centrale ne conserve pas l’orientation dans l’espace.
Le bonhomme lève la main droite et son image lève la main gauche.
Symétrie orthogonale par rapport à une droite
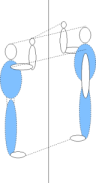
On retrouve la même définition que dans le plan. Une symétrie orthogonale par rapport à une droite est aussi une rotation d’axe (d) et d’angle plat.
Contrairement à ce qui se passe dans le plan, une telle symétrie dans l’espace conserve l’orientation.
Le bonhomme lève la main droite et son image lève la main droite.
Symétrie orthogonale par rapport à un plan

La symétrie orthogonale par rapport au plan (P) est la transformation qui laisse tous les points de (P) invariants et qui, à tout point M non situé sur (P), associe le point M’ tel que (P) soit le plan médiateur de [MM']
Une telle symétrie conserve les distances et les angles, mais ne conserve pas l'orientation.
Par exemple, quand vous levez la main droite devant votre miroir, votre image lève sa main gauche.
On démontre que l'ensemble des symétries par rapport à des plans génère par composition tout l'ensemble des isométries de l'espace.
Les symétries obliques
On peut tout aussi bien définir des symétries d’axe (d) selon la direction (P) ou des symétries par rapport à (P) suivant la direction (d), à condition que tout sous-espace égal ou parallèle à (P) ne contienne pas entièrement (d) ni ne soit entièrement contenu dans (d) et que leur intersection se réduise à un seul point (sinon ces transformations ne sont pas des symétries mais des projections).
Mais ces transformations ne sont pas des isométries si (d) et (P) ne sont pas orthogonaux. Ces transformations (de même que les projections) conservent cependant les barycentres et sont des cas particuliers de transformations affines de l’espace.
Notes et références
Voir aussi
Wikiwand - on
Seamless Wikipedia browsing. On steroids.







