Loading AI tools
El dos (2) es el número natural que sigue al uno y precede al tres.
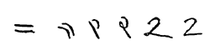
| 2 | |||||
|---|---|---|---|---|---|
| Cardinal | Dos | ||||
| Ordinal | Segundo, -a, 2.º, 2.ª[1] | ||||
| Partitivo | Mitad, medio, -a | ||||
| Multiplicativo | Doble, duplo, -a | ||||
| Factorización | 2 (número primo) | ||||
| Sistemas de numeración | |||||
| Romana | II | ||||
| Arábiga oriental | ٢ | ||||
| Ática | ΙΙ | ||||
| Jónica | β | ||||
| China | 二 | ||||
| China financiera | 貳 | ||||
| Japonesa | 二(ni) | ||||
| Egipcia | II | ||||
| Griega | Βʹ | ||||
| Hebrea | ב | ||||
| Armenia | Բ | ||||
| Maya | •• | ||||
| Cirílica | В | ||||
| De los Campos de Urnas | // | ||||
| India | ௨ | ||||
| Sistema binario | 10 | ||||
| Sistema octal | 2 | ||||
| Sistema hexadecimal | 2 | ||||
| Como parámetro de una función | |||||
| Función φ de Euler | 1 | ||||
| Función divisor | 2 | ||||
| Función de Möbius | -1 | ||||
| Función de Mertens | 0 | ||||
| Potencias de dos | |||||
|
| |||||
| Lista de números | |||||
- El cuerpo de menor cardinal contiene dos elementos.
- Es el valor más pequeño que anula la Función de Mertens.
- Es la característica de Euler para los poliedros.
- Es la base del sistema de numeración más sencillo en que los números naturales pueden escribirse de forma consistente, el sistema binario, empleado sobre todo en el lenguaje de máquina.
- Es la base del logaritmo binario.
- Junto al uno son los únicos números que son iguales a su factorial.
- Junto al uno y el cero, son los únicos números que en todas las bases son números de Harshad.
- Es el único número aparte del 1 que da igual resultado si se multiplica por sí mismo o si se eleva a sí mismo; además que, al sumarlo consigo también da igual resultado que la potenciación y multiplicación por sí mismo, a diferencia del 1 cuya suma es 2. Véase a continuación:
2 ∙ 2 = 4
22 = 4- Su raíz primitiva mínima es 1[2]
- Es el primer:
- Número primo y el único de ellos que es par. Lo sucede el tres.
- Número primo de Eisenstein, sucedido por el cinco.
- Número primo de Sophie Germain, sucedido por el tres.[3]
- Número primo de Stern, sucedido por el tres.
- Número primo factorial, sucedido por el tres.[NOTA 1]
- Número de Lucas, sucedido por el uno.
- Número de Perrin primo, sucedido por el tres. Además aparece dos veces en dicha sucesión, como el tercer y quinto elemento.[4]
- Número de Smarandache–Wellin, sucedido por el veintitrés.
- Primorial, sucedido por el seis.
- Término de la sucesión (1 + 1/n)n, la cual tiene como límite el número e.
- Es el segundo:
- Número de Markov, después del uno y antes del cinco.
- Número de Motzkin, después del uno y antes del cuatro.
- Número de Pell, después del uno y antes del cinco.
- Es el tercer:
- Número de Bell, después del uno y antes del cinco.
- Término de la sucesión de Fibonacci, después del uno y antes del tres.
- Es un número de Catalan.
- Es un número de Pell.


- Es el número atómico del helio.
- Objeto de Messier M2, es un cúmulo globular en la constelación de Acuario.
- El cerebro humano está dividido en dos partes hemisferio derecho e izquierdo.

La menor cantidad de cifras necesarias para definir un sistema de numeración consistente en notación posicional es dos, en donde un símbolo representa al cero o ausencia y otro al uno o presencia. A estos sistemas se los denonomina binarios.
Si bien existen documentos chinos e hindúes de la antigüedad que tratan de sistemas de notación binarias, fue Gottfried Leibniz en el siglo XVII quien sentó las bases del sistema actual, utilizando los símbolos 0 y 1. Posteriormente, George Boole determinó el conjunto de reglas y operaciones que definen a cualquier sistema binario, desarrollando así una rama de la matemática que lleva su nombre: el Álgebra de Boole. Basado en ella, en 1937 el estadounidense Claude Elwood Shannon desarrolló el primer código binario, que es el lenguaje de las computadoras. Llevando así al sistema binario un paso más allá; ahora no solo se pueden representar números con él, sino también escribir textos, realizar imágenes, videos o crear programas informáticos. En fin, con solo dos símbolos se puede crear e interpretar todo el mundo digital, del cual depende gran parte de nuestra actual tecnología.
En diversas corrientes filosóficas y teológicas se afirma la existencia de dos principios fundamentales y basan en ellos su doctrina. Algunas de las características comunes que podemos identificar es que son supremos, increados, independientes, irreductibles y antagónicos. Estos entes suelen ir asociados a conceptos fundamentales como ser el bien y el mal, materia y espíritu, orden físico y orden moral, lo ideal y lo real, lo divino y lo terrenal o lo natural y lo racional.
Entre las teoría dualistas más importantes, debido a su gran influencia en el desarrollo científico y religioso europeo de mediados del siglo XVII, se encuentra el dualismo cartesiano que resuelve un dilema surgido durante el renacimiento sobre el papel divino en la creación y evolución del Universo, al distinguir y separar lo físico de lo espiritual, asignándole el estudio de lo material a las ciencias y el de lo inmaterial a las religiones. Desde el punto de vista cartesiano, lo físico puede conocerse interactuando con él, experimentando, observando; mientras que lo inmaterial juega un rol de andamiaje y sostén imponiendo las reglas del mundo físico sin afectarlo de manera directa. Así, atribuye a Dios la creación del Universo y con él de las leyes que lo rigen, mientras que la física, como ciencia, será quien deba descubrirlas.[5] Debido a la influencia de sus ideas dualistas en el conductismo, es considerado el padre de la psicología moderna.[6]
Véase también: René Descartes

Los organismos vivos presentan una variedad asombrosa de formas. No obstante, existen patrones básicos comunes a todos ellos. Uno de ellos, muy importante para su clasificación, es la simetría de sus cuerpos. Cuando un animal posee una estructura corporal donde sus órganos aparecen duplicados con respecto a un plano que lo divide en dos partes, se dice que tiene simetría bilateral. Se cree que la razón por la cual la mayor parte de las especies zoológicas presentan este tipo de simetría es debido a las ventajas que presenta a la movilidad.
Existen tres planos posibles que sirven de soporte a la simetría bilateral, pudiendo presentarse 1, 2 o los 3 en la misma especie. Ellos son el plano sagital, que divide al cuerpo en sus mitades derecha e izquierda; el plano frontal o coronal, que lo divide en las partes dorsal y ventral (el frente y el reverso) y el plano transversal, que lo divide en sus partes anterior y posterior.[7]
Aquellos organismos que poseen simetría bilateral se encuentran agrupados en el filo Bilateria. Este tipo de organización resultó vital en el desarrollo del sistema nervioso central.
La simetría bilateral también aparece, aunque en menor medida en el reino vegetal. Las hojas, flores y frutos de ciertas especies la poseen. En cambio, saliendo de estos dos reinos es muy difícil de hallar.
Dos puede ser tanto sustantivo («el dos de copas») como adjetivo («dos libros»).
Como adjetivo numeral multiplicativo, solo se usa la forma doble para ambos géneros: «visión doble». Como sustantivo multiplicativo, también existen duplo y dupla, aunque son raramente usados; el femenino dupla persiste en algunos países de América para indicar una pareja o grupo de dos personas o cosas.[8]
Como partitivo o fraccionario, existen las formas mitad y medio (sustantivos): «la mitad de la población», aunque medio solo es normal en un contexto matemático: «la superficie de un triángulo es igual a un medio de la base por su altura». Como adjetivo, solo se usa medio, que debe concordar en género y número con el sustantivo al cual modifica: «dos medias naranjas».[9] Medio es también adverbio (y como tal, invariable) y significa "no completamente": «las ollas están medio llenas».
Existen varios prefijos que significan dos y participan en la construcción de una gran cantidad de palabras de uso cotidiano: bi- / bis- / biz-, di- y du-, como en bisiesto, dicotomía y dual.

- En muchas culturas el 2 se representa mediante dos puntos o dos trazos (horizontales o verticales). Por ejemplo, en la numeración romana (II) y en la numeración china (二).
- Considerado por los pitagóricos como el primer número en sentido estricto, ya que representa la primaria pluralidad posible: si el uno corresponde al ser creador, el dos es la primera y más elemental manifestación de la creación. Es la dualidad la que posibilita la pluralidad, en tanto que dos son los principios contrarios creados que hacen posible el resto: masculino y femenino, el cielo y la tierra, la luz y la oscuridad, etc.
- Según la leyenda cabalística el número dos expresa en el orden moral el hombre y la mujer, y en el físico la causa eficiente y la materia.
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.