EO
All
Articles
Dictionary
Quotes
Map

Wikiwand ❤️ Wikipedia

PrivacyTerms

Hiperbola funkcio

hiperbola analogaĵo de la trigonometriaj funkcioj From Wikipedia, the free encyclopedia

Hiperbola funkcio
DifinojProprecojDerivaĵojMalderivaĵojSeriojHiperbolaj funkcioj por kompleksaj nombrojSimileco al trigonometriaj funkciojVidu ankaŭEksteraj ligiloj

En matematiko, la hiperbolaj funkcioj estas certaj funkcioj de unu variablo, iel analogaj al la ordinaraj trigonometriaj funkcioj.

Polurinda artikolo
 Ĉi tiu artikolo bezonas poluradon, ĉar ĝi montras stilajn kaj/aŭ gramatikajn kaj/aŭ strukturajn problemojn, kiuj ne konformas al stilogvido.
La priskribo de la problemo troviĝas ĉi tie. Bonvolu ŝanĝi la enhavon por plibonigi la artikolon.
Pliaj informoj Matematikaj funkcioj, Fundamentaj funkcioj ...
Matematikaj funkcioj
Aroj: fonta aro, argumentaro, bildaro, cela aro (suma klarigo) • malbildo
Fundamentaj funkcioj
Algebraj funkcioj:
konstanta • lineara • kvadrata • polinoma • racionala • Transformo de Möbius
Aliaj funkcioj:
trigonometriaj • inversa trigonometria • hiperbola • eksponenta • logaritma • potenca
Specialaj funkcioj
erara • β • Γ • ζ • η • W de Lambert • de Bessel
Nombroteoriaj funkcioj:
τ • σ • de Möbius • φ • π • λ
Ecoj:
totaleco kaj parteco • pareco kaj malpareco • monotoneco • bariteco • periodeco • disĵeteco • surĵeteco • dissurĵeteco
kontinueco • derivaĵeco • integralebleco
Fermi

Iliaj retroĵetoj estas la inversaj hiperbolaj funkcioj.

La bazaj hiperbolaj funkcioj estas la hiperbola sinuso kaj hiperbola kosinuso, difinitaj per eksponenta funkcio. La aliaj hiperbolaj funkcioj estas difinitaj per ili du, simile al tio kiel per sinuso kaj kosinuso estas difinitaj la aliaj trigonometriaj funkcioj

La hiperbolaj funkcioj preni reelajn valorojn por reelaj argumentoj. La argumento estas iam nomata kiel la hiperbola angulo. En kompleksa analitiko, ili estas simple racionalaj funkcioj de eksponentaj funkcioj, kaj do estas meromorfaj funkcioj.

La grafikaĵo de hiperbola kosinuso estas la kateno, la kurbo formata per fleksebla ĉeno de egala longa denseco, fiksita je siaj finoj kaj pendanta libere sub gravito.

La hiperbolaj funkcioj estas:

Pliaj informoj , ...
NomoSkribmanieroDifino
Hiperbola sinuso sinh x aŭ sh x e x − e − x 2 {\displaystyle {\frac {e^{x}-e^{-x}}{2}}\!} {\displaystyle {\frac {e^{x}-e^{-x}}{2}}\!}
Hiperbola kosinuso cosh x aŭ ch x e x + e − x 2 {\displaystyle {\frac {e^{x}+e^{-x}}{2}}\!} {\displaystyle {\frac {e^{x}+e^{-x}}{2}}\!}
Hiperbola tangento tanh x aŭ th x sinh ⁡ x cosh ⁡ x {\displaystyle {\frac {\sinh x}{\cosh x}}\!} {\displaystyle {\frac {\sinh x}{\cosh x}}\!}
Hiperbola kotangento coth x aŭ cth x cosh ⁡ x sinh ⁡ x {\displaystyle {\frac {\cosh x}{\sinh x}}\!} {\displaystyle {\frac {\cosh x}{\sinh x}}\!}
Hiperbola sekanto sech x 1 cosh ⁡ x {\displaystyle {\frac {1}{\cosh x}}\!} {\displaystyle {\frac {1}{\cosh x}}\!}
Hiperbola kosekanto csch 1 sinh ⁡ x {\displaystyle {\frac {1}{\sinh x}}\!} {\displaystyle {\frac {1}{\sinh x}}\!}
Fermi

sinh, cosh, tanh
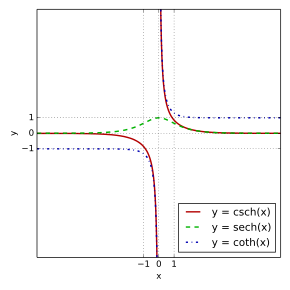csch, sech, coth
sinh ⁡ x = e x − e − x 2 = − i sin ⁡ i x {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}=-i\sin ix\!} {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}=-i\sin ix\!}
cosh ⁡ x = e x + e − x 2 = cos ⁡ i x {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}=\cos ix\!} {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}=\cos ix\!}
tanh ⁡ x = sinh ⁡ x cosh ⁡ x = e x − e − x 2 e x + e − x 2 = e x − e − x e x + e − x = e 2 x − 1 e 2 x + 1 = − i tan ⁡ i x {\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {\frac {e^{x}-e^{-x}}{2}}{\frac {e^{x}+e^{-x}}{2}}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}=-i\tan ix\!} {\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {\frac {e^{x}-e^{-x}}{2}}{\frac {e^{x}+e^{-x}}{2}}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}=-i\tan ix\!}
coth ⁡ x = cosh ⁡ x sinh ⁡ x = e x + e − x 2 e x − e − x 2 = e x + e − x e x − e − x = e 2 x + 1 e 2 x − 1 = i cot ⁡ i x {\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {\frac {e^{x}+e^{-x}}{2}}{\frac {e^{x}-e^{-x}}{2}}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}=i\cot ix\!} {\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {\frac {e^{x}+e^{-x}}{2}}{\frac {e^{x}-e^{-x}}{2}}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}=i\cot ix\!}
sech ⁡ x = 1 cosh ⁡ x = 2 e x + e − x = sec ⁡ i x {\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}=\sec {ix}\!} {\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}=\sec {ix}\!}
csch ⁡ x = 1 sinh ⁡ x = 2 e x − e − x = i csc i x {\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}=i\,\csc \,ix\!} {\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}=i\,\csc \,ix\!}
( cosh ⁡ t ) 2 − ( sinh ⁡ t ) 2 = 1 {\displaystyle (\cosh t)^{2}-(\sinh t)^{2}=1\!} {\displaystyle (\cosh t)^{2}-(\sinh t)^{2}=1\!}
( tanh ⁡ x ) 2 = 1 − ( sech ⁡ x ) 2 {\displaystyle (\tanh x)^{2}=1-(\operatorname {sech} x)^{2}\!} {\displaystyle (\tanh x)^{2}=1-(\operatorname {sech} x)^{2}\!}
( coth ⁡ x ) 2 = 1 + ( csch ⁡ x ) 2 {\displaystyle (\coth x)^{2}=1+(\operatorname {csch} x)^{2}\!} {\displaystyle (\coth x)^{2}=1+(\operatorname {csch} x)^{2}\!}

kie i estas la imaginara unuo.

sinh(-x) = -sinh x
cosh(-x) = cosh x

De ĉi tie:

tanh(-x) = -tanh x
coth(-x) = -coth x
sech(-x) = sech x
csch(-x) = -csch x

cosh x kaj sech x estas paraj funkcioj, la aliaj el la ses estas neparaj funkcioj.

Identoj por sumo de argumentoj:

sinh ⁡ ( x + y ) = sinh ⁡ x cosh ⁡ y + cosh ⁡ x sinh ⁡ y {\displaystyle \sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y\,} {\displaystyle \sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y\,}
cosh ⁡ ( x + y ) = cosh ⁡ x cosh ⁡ y + sinh ⁡ x sinh ⁡ y {\displaystyle \cosh(x+y)=\cosh x\cosh y+\sinh x\sinh y\,} {\displaystyle \cosh(x+y)=\cosh x\cosh y+\sinh x\sinh y\,}
tanh ⁡ ( x + y ) = tanh ⁡ x + tanh ⁡ y 1 + tanh ⁡ x tanh ⁡ y {\displaystyle \tanh(x+y)={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\,} {\displaystyle \tanh(x+y)={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\,}

por duoblaj argumentoj:

sinh ⁡ 2 x   = 2 sinh ⁡ x cosh ⁡ x {\displaystyle \sinh 2x\ =2\sinh x\cosh x\,} {\displaystyle \sinh 2x\ =2\sinh x\cosh x\,}
cosh ⁡ 2 x   = ( cosh ⁡ x ) 2 + ( sinh ⁡ x ) 2 = 2 ( cosh ⁡ x ) 2 − 1 = 2 ( sinh ⁡ x ) 2 + 1 {\displaystyle \cosh 2x\ =(\cosh x)^{2}+(\sinh x)^{2}=2(\cosh x)^{2}-1=2(\sinh x)^{2}+1\,} {\displaystyle \cosh 2x\ =(\cosh x)^{2}+(\sinh x)^{2}=2(\cosh x)^{2}-1=2(\sinh x)^{2}+1\,}

por duonaj argumentoj:

( cosh ⁡ x 2 ) 2 = cosh ⁡ x + 1 2 {\displaystyle \left(\cosh {\frac {x}{2}}\right)^{2}={\frac {\cosh x+1}{2}}} {\displaystyle \left(\cosh {\frac {x}{2}}\right)^{2}={\frac {\cosh x+1}{2}}}
( sinh ⁡ x 2 ) 2 = cosh ⁡ x − 1 2 {\displaystyle \left(\sinh {\frac {x}{2}}\right)^{2}={\frac {\cosh x-1}{2}}} {\displaystyle \left(\sinh {\frac {x}{2}}\right)^{2}={\frac {\cosh x-1}{2}}}
d sinh ⁡ ( x ) d x = cosh ⁡ ( x ) {\displaystyle {\frac {d\sinh(x)}{dx}}=\cosh(x)\,} {\displaystyle {\frac {d\sinh(x)}{dx}}=\cosh(x)\,}
d cosh ⁡ ( x ) d x = sinh ⁡ ( x ) {\displaystyle {\frac {d\cosh(x)}{dx}}=\sinh(x)\,} {\displaystyle {\frac {d\cosh(x)}{dx}}=\sinh(x)\,}
d tanh ⁡ ( x ) d x = 1 − ( tanh ⁡ ( x ) ) 2 = ( sech ⁡ ( x ) ) 2 = 1 / ( cosh ⁡ ( x ) ) 2 {\displaystyle {\frac {d\tanh(x)}{dx}}=1-(\tanh(x))^{2}=(\operatorname {sech} (x))^{2}=1/(\cosh(x))^{2}\,} {\displaystyle {\frac {d\tanh(x)}{dx}}=1-(\tanh(x))^{2}=(\operatorname {sech} (x))^{2}=1/(\cosh(x))^{2}\,}
d coth ⁡ ( x ) d x = 1 − ( coth ⁡ ( x ) ) 2 = − ( csch ⁡ ( x ) ) 2 = − 1 / ( sinh ⁡ ( x ) ) 2 {\displaystyle {\frac {d\coth(x)}{dx}}=1-(\coth(x))^{2}=-(\operatorname {csch} (x))^{2}=-1/(\sinh(x))^{2}\,} {\displaystyle {\frac {d\coth(x)}{dx}}=1-(\coth(x))^{2}=-(\operatorname {csch} (x))^{2}=-1/(\sinh(x))^{2}\,}
d c s c h ( x ) d x = − coth ⁡ ( x ) c s c h ( x ) {\displaystyle {\frac {d\operatorname {csch(x)} }{dx}}=-\coth(x)\operatorname {csch(x)} \,} {\displaystyle {\frac {d\operatorname {csch(x)} }{dx}}=-\coth(x)\operatorname {csch(x)} \,}
d s e c h ( x ) d x = − tanh ⁡ ( x ) s e c h ( x ) {\displaystyle {\frac {d\operatorname {sech(x)} }{dx}}=-\tanh(x)\operatorname {sech(x)} \,} {\displaystyle {\frac {d\operatorname {sech(x)} }{dx}}=-\tanh(x)\operatorname {sech(x)} \,}
∫ sinh ⁡ a x d x = 1 a cosh ⁡ a x + C {\displaystyle \int \sinh ax\,dx={\frac {1}{a}}\cosh ax+C} {\displaystyle \int \sinh ax\,dx={\frac {1}{a}}\cosh ax+C}
∫ cosh ⁡ a x d x = 1 a sinh ⁡ a x + C {\displaystyle \int \cosh ax\,dx={\frac {1}{a}}\sinh ax+C} {\displaystyle \int \cosh ax\,dx={\frac {1}{a}}\sinh ax+C}
∫ tanh ⁡ a x d x = 1 a ln ⁡ ( cosh ⁡ a x ) + C {\displaystyle \int \tanh ax\,dx={\frac {1}{a}}\ln(\cosh ax)+C} {\displaystyle \int \tanh ax\,dx={\frac {1}{a}}\ln(\cosh ax)+C}
∫ coth ⁡ a x d x = 1 a ln ⁡ ( sinh ⁡ a x ) + C {\displaystyle \int \coth ax\,dx={\frac {1}{a}}\ln(\sinh ax)+C} {\displaystyle \int \coth ax\,dx={\frac {1}{a}}\ln(\sinh ax)+C}

En la pli supre donitaj esprimoj, C estas la konstanto de integralado.

Serioj de Taylor:

sinh ⁡ x = x + x 3 3 ! + x 5 5 ! + x 7 7 ! + ⋯ = ∑ n = 0 ∞ x 2 n + 1 ( 2 n + 1 ) ! {\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}} {\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}
cosh ⁡ x = 1 + x 2 2 ! + x 4 4 ! + x 6 6 ! + ⋯ = ∑ n = 0 ∞ x 2 n ( 2 n ) ! {\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}} {\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}
tanh ⁡ x = x − x 3 3 + 2 x 5 15 − 17 x 7 315 + ⋯ = ∑ n = 1 ∞ 2 2 n ( 2 2 n − 1 ) B 2 n x 2 n − 1 ( 2 n ) ! , | x | < π 2 {\displaystyle \tanh x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}} {\displaystyle \tanh x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}
sech x = 1 − x 2 2 + 5 x 4 24 − 61 x 6 720 + ⋯ = ∑ n = 0 ∞ E 2 n x 2 n ( 2 n ) ! , | x | < π 2 {\displaystyle \operatorname {sech} \,x=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}} {\displaystyle \operatorname {sech} \,x=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}

Hiperbola kotangento kaj hiperbola kosekanto havas poluson en punkto 0, tiel iliaj seriaj elvolvaĵoj estas serioj de Laurent:

coth ⁡ x = 1 x + x 3 − x 3 45 + 2 x 5 945 + ⋯ = 1 x + ∑ n = 1 ∞ 2 2 n B 2 n x 2 n − 1 ( 2 n ) ! , 0 < | x | < π {\displaystyle \coth x={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi } {\displaystyle \coth x={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi } (serio de Laurent)
csch x = 1 x − x 6 + 7 x 3 360 − 31 x 5 15120 + ⋯ = 1 x + ∑ n = 1 ∞ 2 ( 1 − 2 2 n − 1 ) B 2 n x 2 n − 1 ( 2 n ) ! , 0 < | x | < π {\displaystyle \operatorname {csch} \,x={\frac {1}{x}}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi } {\displaystyle \operatorname {csch} \,x={\frac {1}{x}}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }

En la formuloj pli supre

Bn estas la n-a nombro de Bernoulli,
En estas la n-a eŭlera nombro.

Pro tio ke la eksponenta funkcio estas difinita por ĉiu kompleksa argumento, la difinoj de la hiperbolaj funkcioj uzeblas ankaŭ por kompleksaj argumentoj. La funkcioj sinh z kaj cosh z estas tiam holomorfaj; iliaj serioj de Taylor konverĝas ĉie.

Interrilatoj al trigonometriaj funkcioj estas donitaj per eŭlera formulo, vera por ĉiu kompleksa x:

eix = cos x + i sin x

el ĉi tiu formulo sekvas la sekva formulo

e−ix = cos x - i sin x

kaj tiel

cosh ⁡ i x = e i x + e − i x 2 = cos ⁡ x {\displaystyle \cosh ix={\frac {e^{ix}+e^{-ix}}{2}}=\cos x} {\displaystyle \cosh ix={\frac {e^{ix}+e^{-ix}}{2}}=\cos x}
sinh ⁡ i x = e i x − e − i x 2 = i sin ⁡ x {\displaystyle \sinh ix={\frac {e^{ix}-e^{-ix}}{2}}=i\sin x} {\displaystyle \sinh ix={\frac {e^{ix}-e^{-ix}}{2}}=i\sin x}
tanh ix = i tan x
cosh x = cos ix
sinh x = -i sin ix
tanh x = -i tan ix

La hiperbolaj funkcioj estas perioda kun kompleksa periodo 2πi (πi por hiperbola tangento kaj hiperbola kotangento).

De la difinoj de hiperbolaj sinuso kaj kosinuso, eblas derivi jenajn identojn:

ex = cosh x + sinh x

kaj

e−x = cosh x - sinh x

Ĉi tiuj esprimoj estas analogoj al la eŭlera formulo.

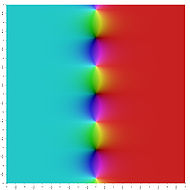Thumb
sinh z		 Thumb
tanh z		 Thumb
sech z
Thumb
cosh z		 Thumb
coth z		 Thumb
csch z
Thumb
Radio tra la origino tranĉas la hiperbolon x2-y2 = 1 en la punkto (cosh A, sinh A), kie A estas la areo inter la radio kaj ĝia spegula bildo kun respekto al la x-akso, kaj la hiperbolo

Punkto sur la hiperbolo x y = 1 kun x > 1 difinas hiperbolan triangulon en kiu la flanko najbara al la hiperbola angulo estas asociita kun cosh kaj la flanko kontraŭa estas asociita kun sinh. Pro tio ke la punkto (1, 1) sur ĉi tiu hiperbolo estas je distanco √2 de la punkto (0, 0), la normaliga konstanto 1/√2 estas necesa al difini funkciojn cosh kaj sinh per longoj de la flankoj de la hiperbola triangulo.

Simile al tio ke kiel la aro de punktoj (cos t, sin t) estas cirklo, la aro de punktoj (cosh t, sinh t) estas la dekstra duono de la egallatera hiperbolo x2-y2 = 1.

La parametro t estas ne cirkla angulo, sed hiperbola angulo kiu estas duobligita areo inter la x-akso, la hiperbolo kaj la rekto tra punktoj (0, 0) kaj (cosh t, sinh t). Traktado de la parametro kiel duobligita areo fakte taŭgas ankaŭ por la trigonometriaj funkcioj; se konsideri punkton (cos t, sin t) sur cirklo do la argumento t estas duobligita areo de la cirkla sektoro inter la x-akso, la cirklo kaj la rekto tra punktoj (0, 0) kaj (cos t, sin t).

La hiperbolaj funkcioj kontentigas multajn identojn, similajn en formo al tiuj por la trigonometriaj funkcioj. Fakte, regulo de Osborn statas ke eblas konverti ĉiun trigonometrian identon en hiperbolan identon per elvolvanta ĝin plene en termojn de entjeraj potencoj de sinusoj kaj kosinusoj, ŝanĝo de sin al sinh kaj cos al cosh, kaj ŝanĝo de la signo de ĉiu termo kiu enhavas produton de kvanto 2, 6, 10, 14, ... da sinh-oj, kalkulante kun la potencoj. La derivado povas esti farita per trairo al trigonometriaj funkcioj kiel estas donite pli supre. Oni fari anstataŭigon en la fonta trigonometria idento kiel cosh ixj = cos xj kaj sinh ixj = i sin xj por ĉiu variablo xj; ĉi tiu aldona multiplikata imaginara unuo i ĉe sinuso, se en potenco 2, 6, 10, 14, ..., donas la ŝanĝon de signo. Poste necesas ŝanĝi la variablojn wj = ixj kaj la hiperbola idento rezultiĝas.

Ĉi tiel eblas ricevi donitajn pli supre identojn por sumo de argumentoj, por duoblaj argumentoj kaj por duonaj argumentoj

La funkcio de Gudermannian donas interrilaton inter la trigonometriaj kaj la hiperbolaj funkcioj ne engaĝante kompleksajn nombrojn.

  • Hiperbolo
  • Inversa hiperbola funkcio
  • Trigonometria funkcio
  • Inversa trigonometria funkcio
  • Eksponenta funkcio
  • Eŭlera formulo
  • Funkcio de Gudermannian
  • Kateno
  • Kategorio Hiperbola funkcio en la Vikimedia Komunejo (Multrimedaj datumoj)
  • Mnemoniko por hiperbolaj formuloj. G. Osborn, La Matematika Gazeto, p. 189, volumo 2, eldono 34, julio 1902 (la regulo de Osborn)
  • Hiperbolaj funkcioj Arkivigite je 2012-02-18 per la retarkivo Wayback Machine je PlanetMath
  • Hiperbolaj funkcioj je MathWorld
  • Hiperbola tandento je MathWorld
  • GonioLab Arkivigite je 2007-10-06 per la retarkivo Wayback Machine: Videbligo de la unuobla cirklo, trigonometriaj kaj hiperbolaj funkcioj
  • TTT-kalkulilo de hiperbolaj funkcioj
Edit in WikipediaRevision historyRead in Wikipedia

Wikiwand in your browser!

Seamless Wikipedia browsing. On steroids.

Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.

Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.

Chrome
Wikiwand for Chrome
Edge
Wikiwand for Edge
Firefox
Wikiwand for Firefox

Difinoj

Proprecoj

Derivaĵoj

Malderivaĵoj

Serioj

Hiperbolaj funkcioj por kompleksaj nombroj

Simileco al trigonometriaj funkcioj

Vidu ankaŭ

Eksteraj ligiloj