Hexagonal tiling

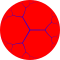
In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} (as a truncated triangular tiling).

Hexagonal tiling
Type	regular tiling
Tile	regular hexagon
Vertex configuration	6.6.6
Wallpaper group	p6m
Dual	triangular tiling
Properties	vertex-transitive, edge-transitive, face-transitive

English mathematician John Conway called it a hextille.

The internal angle of the hexagon is 120 degrees, so three hexagons at a point make a full 360 degrees. It is one of three regular tilings of the plane. The other two are the triangular tiling and the square tiling.

Structure and properties

The hexagonal tiling has a structure consisting of a regular hexagon only as its prototile, sharing two vertices with other identical ones, an example of monohedral tiling.^[1] Each vertex at the tiling is surrounded by three regular hexagons, denoted as ${\displaystyle 6.6.6}$ by vertex configuration.^[2] The dual of a hexagonal tiling is triangular tiling, because the center of each hexagonal tiling connects to another center of one, forming equilateral triangles.^[3]

Every mutually incident vertex, edge, and tile of a hexagonal tiling can be act transitively to another of those three by mapping the first ones to the second through the symmetry operation. In other words, they are vertex-transitive (mapping the vertex of a tile to another), edge-transitive (mapping the edge to another), and face-transitive (mapping regular hexagonal tile to another). From these, the hexagonal tiling is categorized as one of three regular tilings; the remaining being its dual and square tiling..^[4] The symmetry group of a hexagonal tiling is p6m.^[5]

Applications

The densest circle packing is arranged like the hexagons in this tiling

If a circle is inscribed in each hexagon, the resulting figure is the densest way to arrange circles in two dimensions; its packing density is ${\textstyle {\frac {\pi }{2{\sqrt {3}}}}\approx 0.907}$.^[6] The honeycomb conjecture states that hexagonal tiling is the best way to divide a surface into regions of equal area with the least total perimeter.^[7] The optimal three-dimensional structure for making honeycomb (or rather, soap bubbles) was investigated by Lord Kelvin, who believed that the Kelvin structure (or body-centered cubic lattice) is optimal. However, the less regular Weaire–Phelan structure is slightly better.

Graphene

Chicken wire fencing

The hexagonal tiling is commonly found in nature, such as the sheet of graphene with strong covalent carbon bonds. Tubular graphene sheets have been synthesised, known as carbon nanotubes.^[8] They have many potential applications, due to their high tensile strength and electrical properties. Silicene has a similar structure as graphene.

Chicken wire consists of a hexagonal lattice of wires, although the shape is not regular.^[9]

• 
  A carbon nanotube can be seen as a hexagon tiling on a cylindrical surface
• 
  Hexagonal Persian tile c. 1955
• 
  Hexagonal trylinka pavement crumbling in New York

The hexagonal tiling appears in many crystals. In three dimensions, the face-centered cubic and hexagonal close packing are common crystal structures. They are the densest sphere packings in three dimensions. Structurally, they comprise parallel layers of hexagonal tilings, similar to the structure of graphite. They differ in the way that the layers are staggered from each other, with the face-centered cubic being the more regular of the two. Pure copper, amongst other materials, forms a face-centered cubic lattice.

Uniform colorings

There are three distinct uniform colorings of a hexagonal tiling, all generated from reflective symmetry of Wythoff constructions. The (h,k) represent the periodic repeat of one colored tile, counting hexagonal distances as h first, and k second. The same counting is used in the Goldberg polyhedra, with a notation {p+,3}_h,k, and can be applied to hyperbolic tilings for p > 6.

k-uniform	1-uniform			2-uniform		3-uniform
Symmetry	p6m, (*632)		p3m1, (*333)	p6m, (*632)		p6, (632)
Picture
Colors	1	2	3	2	4	2	7
(h,k)	(1,0)	(1,1)		(2,0)		(2,1)
Schläfli	{6,3}	t{3,6}	t{3[3]}
Wythoff	3 | 6 2	2 6 | 3	3 3 3 |
Coxeter
Conway	H	tΔ		cH=t6daH		wH=t6dsH

The 3-color tiling is a tessellation generated by the order-3 permutohedrons.

Chamfered hexagonal tiling

A chamfered hexagonal tiling replaces edges with new hexagons and transforms into another hexagonal tiling. In the limit, the original faces disappear, and the new hexagons degenerate into rhombi, and it becomes a rhombic tiling.

The chamfered hexagonal tiling degenerates into a rhombille tiling at the limit

Hexagons (H)	Chamfered hexagons (cH)			Rhombi (daH)

Related tilings

The hexagons can be dissected into sets of 6 triangles. This process leads to two 2-uniform tilings, and the triangular tiling:

Regular tiling	Dissection	2-uniform tilings		Regular tiling	Inset	Dual Tilings
Original		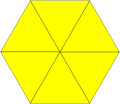1/3 dissected	2/3 dissected	fully dissected		E to IH to FH to H

The hexagonal tiling can be considered an elongated rhombic tiling, where each vertex of the rhombic tiling is stretched into a new edge. This is similar to the relation of the rhombic dodecahedron and the rhombo-hexagonal dodecahedron tessellations in 3 dimensions.

Rhombic tiling

Hexagonal tiling

Fencing uses this relation

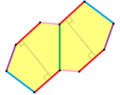
It is also possible to subdivide the prototiles of certain hexagonal tilings by two, three, four or nine equal pentagons:

Pentagonal tiling type 1 with overlays of regular hexagons (each comprising 2 pentagons).

pentagonal tiling type 3 with overlays of regular hexagons (each comprising 3 pentagons).

Pentagonal tiling type 4 with overlays of semiregular hexagons (each comprising 4 pentagons).

Pentagonal tiling type 3 with overlays of two sizes of regular hexagons (comprising 3 and 9 pentagons respectively).

Symmetry mutations

This tiling is topologically related as a part of a sequence of regular tilings with hexagonal faces, starting with the hexagonal tiling, with Schläfli symbol {6,n}, and Coxeter diagram , progressing to infinity.

*n62 symmetry mutation of regular tilings: {6,n} v t e
Spherical	Euclidean	Hyperbolic tilings
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

This tiling is topologically related to regular polyhedra with vertex figure n³, as a part of a sequence that continues into the hyperbolic plane.

*n32 symmetry mutation of regular tilings: {n,3} v t e
Spherical				Euclidean	Compact hyperb.		Paraco.	Noncompact hyperbolic
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

It is similarly related to the uniform truncated polyhedra with vertex figure n.6.6.

*n32 symmetry mutation of truncated tilings: n.6.6 v t e
Sym. *n42 [n,3]	Spherical				Euclid.	Compact		Parac.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis figures
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

This tiling is also part of a sequence of truncated rhombic polyhedra and tilings with [n,3] Coxeter group symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares. The truncated forms have regular n-gons at the truncated vertices, and nonregular hexagonal faces.

Symmetry mutations of dual quasiregular tilings: V(3.n)2
*n32	Spherical			Euclidean	Hyperbolic
	*332	*432	*532	*632	*732	*832...	*∞32
Tiling
Conf.	V(3.3)2	V(3.4)2	V(3.5)2	V(3.6)2	V(3.7)2	V(3.8)2	V(3.∞)2

Monohedral convex hexagonal tilings

There are 3 types of monohedral convex hexagonal tilings.^[10] They are all isohedral. Each has parametric variations within a fixed symmetry. Type 2 contains glide reflections, and is 2-isohedral keeping chiral pairs distinct.

3 types of monohedral convex hexagonal tilings

1	2		3
p2, 2222	pgg, 22×	p2, 2222	p3, 333
b = e B + C + D = 360°	b = e, d = f B + C + E = 360°		a = f, b = c, d = e B = D = F = 120°
2-tile lattice	4-tile lattice		3-tile lattice

There are also 15 monohedral convex pentagonal tilings, as well as all quadrilaterals and triangles.

Topologically equivalent tilings

Hexagonal tilings can be made with the identical {6,3} topology as the regular tiling (3 hexagons around every vertex). With isohedral faces, there are 13 variations. Symmetry given assumes all faces are the same color. Colors here represent the lattice positions.^[11] Single-color (1-tile) lattices are parallelogon hexagons.

13 isohedrally-tiled hexagons

pg (××)		p2 (2222)	p3 (333)	pmg (22*)
pgg (22×)			p31m (3*3)	p2 (2222)	cmm (2*22)	p6m (*632)

Other isohedrally-tiled topological hexagonal tilings are seen as quadrilaterals and pentagons that are not edge-to-edge, but interpreted as colinear adjacent edges:

Isohedrally-tiled quadrilaterals

pmg (22*)		pgg (22×)			cmm (2*22)	p2 (2222)
Parallelogram	Trapezoid	Parallelogram	Rectangle	Parallelogram	Rectangle	Rectangle

Isohedrally-tiled pentagons

p2 (2222)	pgg (22×)	p3 (333)

The 2-uniform and 3-uniform tessellations have a rotational degree of freedom which distorts 2/3 of the hexagons, including a colinear case that can also be seen as a non-edge-to-edge tiling of hexagons and larger triangles.^[12]

It can also be distorted into a chiral 4-colored tri-directional weaved pattern, distorting some hexagons into parallelograms. The weaved pattern with 2 colored faces has rotational 632 (p6) symmetry. A chevron pattern has pmg (22*) symmetry, which is lowered to p1 (°) with 3 or 4 colored tiles.

Regular	Gyrated	Regular	Weaved	Chevron
p6m, (*632)	p6, (632)	p6m (*632)	p6 (632)	p1 (°)
p3m1, (*333)	p3, (333)	p6m (*632)	p2 (2222)	p1 (°)

Circle packing

The hexagonal tiling can be used as a circle packing, placing equal-diameter circles at the center of every point. Every circle is in contact with 3 other circles in the packing (kissing number).^[13] The gap inside each hexagon allows for one circle, creating the densest packing from the triangular tiling, with each circle in contact with a maximum of 6 circles.

Related regular complex apeirogons

There are 2 regular complex apeirogons, sharing the vertices of the hexagonal tiling. Regular complex apeirogons have vertices and edges, where edges can contain 2 or more vertices. Regular apeirogons p{q}r are constrained by: 1/p + 2/q + 1/r = 1. Edges have p vertices, and vertex figures are r-gonal.^[14]

The first is made of 2-edges, three around every vertex, the second has hexagonal edges, three around every vertex. A third complex apeirogon, sharing the same vertices, is quasiregular, which alternates 2-edges and 6-edges.

2{12}3 or	6{4}3 or

See also

• Hexagonal lattice
• Hexagonal prismatic honeycomb
• Tilings of regular polygons
• List of uniform tilings
• List of regular polytopes
• Hexagonal tiling honeycomb
• Hex map board game design