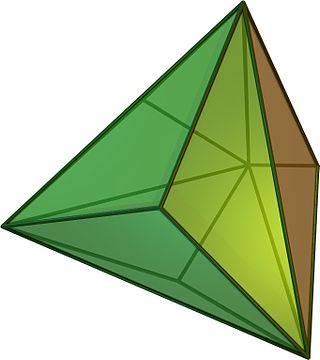
Triakis tetrahedron

In geometry, a triakis tetrahedron (or tristetrahedron^[1], or kistetrahedron^[2]) is a solid constructed by attaching four triangular pyramids onto the triangular faces of a regular tetrahedron, a Kleetope of a tetrahedron.^[3] This replaces the equilateral triangular faces of the regular tetrahedron with three isosceles triangles at each face, so there are twelve in total; eight vertices and eighteen edges form them.^[4] This interpretation is also expressed in the name, triakis, which is used for Kleetopes of polyhedra with triangular faces.^[2]

Triakis tetrahedron
Type	Catalan solid, Kleetope
Faces	12
Edges	18
Vertices	8
Symmetry group	tetrahedral symmetry ${\displaystyle \mathrm {T} _{\mathrm {d} }}$
Dihedral angle (degrees)	129.52°
Dual polyhedron	truncated tetrahedron
Properties	convex, face-transitive, Rupert property
Net

3D model of a triakis tetrahedron

The triakis tetrahedron is a Catalan solid, the dual polyhedron of a truncated tetrahedron, an Archimedean solid with four hexagonal and four triangular faces, constructed by cutting off the vertices of a regular tetrahedron; it shares the same symmetry of full tetrahedral ${\displaystyle \mathrm {T} _{\mathrm {d} }}$. Each dihedral angle between triangular faces is ${\displaystyle \arccos(-7/11)\approx 129.52^{\circ }}$.^[4] Unlike its dual, the truncated tetrahedron is not vertex-transitive, but rather face-transitive, meaning its solid appearance is unchanged by any transformation like reflecting and rotation between two triangular faces.^[5] Whenever a triakis tetrahedron has a hole, it is possible for a polyhedron to exist with the same or larger size passing through it.^[6]

A triakis tetrahedron is different from an augmented tetrahedron as latter is obtained by augmenting the four faces of a tetrahedron with four regular tetrahedra (instead of nonuniform triangular pyramids) resulting in an equilateral polyhedron which is a concave deltahedron (whose all faces are congruent equilateral triangles). The convex hull of an augmented tetrahedron is a triakis tetrahedron.^[7]

See also

• Truncated triakis tetrahedron