Hexagonal lattice
One of the five 2D Bravais lattices From Wikipedia, the free encyclopedia
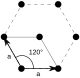
The hexagonal lattice (sometimes called triangular lattice) is one of the five two-dimensional Bravais lattice types.[1] The symmetry category of the lattice is wallpaper group p6m. The primitive translation vectors of the hexagonal lattice form an angle of 120° and are of equal lengths,
The reciprocal lattice of the hexagonal lattice is a hexagonal lattice in reciprocal space with orientation changed by 90° and primitive lattice vectors of length
Honeycomb point set

The honeycomb point set is a special case of the hexagonal lattice with a two-atom basis.[1] The centers of the hexagons of a honeycomb form a hexagonal lattice, and the honeycomb point set can be seen as the union of two offset hexagonal lattices.
In nature, carbon atoms of the two-dimensional material graphene are arranged in a honeycomb point set.
Crystal classes
The hexagonal lattice class names, Schönflies notation, Hermann-Mauguin notation, orbifold notation, Coxeter notation, and wallpaper groups are listed in the table below.
| Geometric class, point group | Wallpaper groups | ||||
|---|---|---|---|---|---|
| Schön. | Intl | Orb. | Cox. | ||
| C3 | 3 | (33) | [3]+ | p3 (333) |
|
| D3 | 3m | (*33) | [3] | p3m1 (*333) |
p31m (3*3) |
| C6 | 6 | (66) | [6]+ | p6 (632) |
|
| D6 | 6mm | (*66) | [6] | p6m (*632) |
|
See also
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.