List of Euclidean uniform tilings

This table shows the 11 convex uniform tilings (regular and semiregular) of the Euclidean plane, and their dual tilings.

An example of uniform tiling in the Archeological Museum of Seville, Sevilla, Spain: rhombitrihexagonal tiling

Uniform tilings and their duals drawn by Max Brückner in Vielecke und Vielflache (1900)

There are three regular and eight semiregular tilings in the plane. The semiregular tilings form new tilings from their duals, each made from one type of irregular face.

John Conway called these uniform duals Catalan tilings, in parallel to the Catalan solid polyhedra.

Uniform tilings are listed by their vertex configuration, the sequence of faces that exist on each vertex. For example 4.8.8 means one square and two octagons on a vertex.

These 11 uniform tilings have 32 different uniform colorings. A uniform coloring allows identical sided polygons at a vertex to be colored differently, while still maintaining vertex-uniformity and transformational congruence between vertices. (Note: Some of the tiling images shown below are not color-uniform.)

In addition to the 11 convex uniform tilings, there are also 14 known nonconvex tilings, using star polygons, and reverse orientation vertex configurations. A further 28 uniform tilings are known using apeirogons. If zigzags are also allowed, there are 23 more known uniform tilings and 10 more known families depending on a parameter: in 8 cases the parameter is continuous, and in the other 2 it is discrete. The set is not known to be complete.

Laves tilings

In the 1987 book, Tilings and patterns, Branko Grünbaum calls the vertex-uniform tilings Archimedean, in parallel to the Archimedean solids. Their dual tilings are called Laves tilings in honor of crystallographer Fritz Laves.^[1][2] They're also called Shubnikov–Laves tilings after Aleksei Shubnikov.^[3] John Conway called the uniform duals Catalan tilings, in parallel to the Catalan solid polyhedra.

The Laves tilings have vertices at the centers of the regular polygons, and edges connecting centers of regular polygons that share an edge. The tiles of the Laves tilings are called planigons. This includes the 3 regular tiles (triangle, square and hexagon) and 8 irregular ones.^[4] Each vertex has edges evenly spaced around it. Three dimensional analogues of the planigons are called stereohedrons.

These dual tilings are listed by their face configuration, the number of faces at each vertex of a face. For example V4.8.8 means isosceles triangle tiles with one corner with four triangles, and two corners containing eight triangles. The orientations of the vertex planigons (up to D₁₂) are consistent with the vertex diagrams in the below sections.

Eleven planigons

Triangles				Quadrilaterals			Pentagons			Hexagon
V63	V4.82	V4.6.12	V3.122	V44	V(3.6)2	V3.4.6.4	V32.4.3.4	V34.6	V33.42	V36

Convex uniform tilings of the Euclidean plane

All reflectional forms can be made by Wythoff constructions, represented by Wythoff symbols, or Coxeter-Dynkin diagrams, each operating upon one of three Schwarz triangle (4,4,2), (6,3,2), or (3,3,3), with symmetry represented by Coxeter groups: [4,4], [6,3], or [3^[3]]. Alternated forms such as the snub can also be represented by special markups within each system. Only one uniform tiling can't be constructed by a Wythoff process, but can be made by an elongation of the triangular tiling. An orthogonal mirror construction [∞,2,∞] also exists, seen as two sets of parallel mirrors making a rectangular fundamental domain. If the domain is square, this symmetry can be doubled by a diagonal mirror into the [4,4] family.

Families:

• (4,4,2), ${\displaystyle {\tilde {BC}}_{2}}$, [4,4] – Symmetry of the regular square tiling
  • ${\displaystyle {\tilde {I}}_{1}^{2}}$, [∞,2,∞]
• (6,3,2), ${\displaystyle {\tilde {G}}_{2}}$, [6,3] – Symmetry of the regular hexagonal tiling and triangular tiling.
  • (3,3,3), ${\displaystyle {\tilde {A}}_{2}}$, [3^[3]]

The [4,4] group family

Uniform tilings (Platonic and Archimedean)	Vertex figure and dual face Wythoff symbol(s) Symmetry group Coxeter diagram(s)	Dual-uniform tilings (called Laves or Catalan tilings)
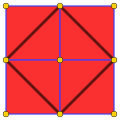Square tiling (quadrille)	4.4.4.4 (or 44) 4 | 2 4 p4m, [4,4], (*442)	self-dual (quadrille)
Truncated square tiling (truncated quadrille)	4.8.8 2 | 4 4 4 4 2 | p4m, [4,4], (*442) or	Tetrakis square tiling (kisquadrille)
Snub square tiling (snub quadrille)	3.3.4.3.4 | 4 4 2 p4g, [4+,4], (4*2) or	Cairo pentagonal tiling (4-fold pentille)

The [6,3] group family

Platonic and Archimedean tilings	Vertex figure and dual face Wythoff symbol(s) Symmetry group Coxeter diagram(s)	Dual Laves tilings
Hexagonal tiling (hextille)	6.6.6 (or 63) 3 | 6 2 2 6 | 3 3 3 3 | p6m, [6,3], (*632)	Triangular tiling (deltille)
Trihexagonal tiling (hexadeltille)	(3.6)2 2 | 6 3 3 3 | 3 p6m, [6,3], (*632) =	Rhombille tiling (rhombille)
Truncated hexagonal tiling (truncated hextille)	3.12.12 2 3 | 6 p6m, [6,3], (*632)	Triakis triangular tiling (kisdeltille)
Triangular tiling (deltille)	3.3.3.3.3.3 (or 36) 6 | 3 2 3 | 3 3 | 3 3 3 p6m, [6,3], (*632) =	Hexagonal tiling (hextille)
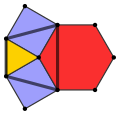Rhombitrihexagonal tiling (rhombihexadeltille)	3.4.6.4 3 | 6 2 p6m, [6,3], (*632)	Deltoidal trihexagonal tiling (tetrille)
Truncated trihexagonal tiling (truncated hexadeltille)	4.6.12 2 6 3 | p6m, [6,3], (*632)	Kisrhombille tiling (kisrhombille)
Snub trihexagonal tiling (snub hextille)	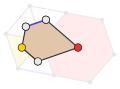3.3.3.3.6 | 6 3 2 p6, [6,3]+, (632)	Floret pentagonal tiling (6-fold pentille)

Non-Wythoffian uniform tiling

Platonic and Archimedean tilings	Vertex figure and dual face Wythoff symbol(s) Symmetry group Coxeter diagram	Dual Laves tilings
Elongated triangular tiling (isosnub quadrille)	3.3.3.4.4 2 | 2 (2 2) cmm, [∞,2+,∞], (2*22)	Prismatic pentagonal tiling (iso(4-)pentille)

Uniform colorings

There are a total of 32 uniform colorings of the 11 uniform tilings:

1. Triangular tiling – 9 uniform colorings, 4 wythoffian, 5 nonwythoffian
   •          
2. Square tiling – 9 colorings: 7 wythoffian, 2 nonwythoffian
   •          
3. Hexagonal tiling – 3 colorings, all wythoffian
   •    
4. Trihexagonal tiling – 2 colorings, both wythoffian
   •   
5. Snub square tiling – 2 colorings, both alternated wythoffian
   •   
6. Truncated square tiling – 2 colorings, both wythoffian
   •   
7. Truncated hexagonal tiling – 1 coloring, wythoffian
   •  
8. Rhombitrihexagonal tiling – 1 coloring, wythoffian
   •  
9. Truncated trihexagonal tiling – 1 coloring, wythoffian
   •  
10. Snub hexagonal tiling – 1 coloring, alternated wythoffian
    •  
11. Elongated triangular tiling – 1 coloring, nonwythoffian
    •  

See also

• Convex uniform honeycomb – The 28 uniform 3-dimensional tessellations, a parallel construction to the convex uniform Euclidean plane tilings.
• Euclidean tilings by convex regular polygons
• List of tessellations
• Percolation threshold
• Uniform tilings in hyperbolic plane