8-demicube

In geometry, a demiocteract or 8-demicube is a uniform 8-polytope, constructed from the 8-hypercube, octeract, with alternated vertices removed. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.

Demiocteract (8-demicube)
Petrie polygon projection
Type	Uniform 8-polytope
Family	demihypercube
Coxeter symbol	151
Schläfli symbols	{3,35,1} = h{4,36} s{21,1,1,1,1,1,1}
Coxeter diagrams	=
7-faces	144: 16 {31,4,1} 128 {36}
6-faces	112 {31,3,1} 1024 {35}
5-faces	448 {31,2,1} 3584 {34}
4-faces	1120 {31,1,1} 7168 {3,3,3}
Cells	10752: 1792 {31,0,1} 8960 {3,3}
Faces	7168 {3}
Edges	1792
Vertices	128
Vertex figure	Rectified 7-simplex
Symmetry group	D8, [35,1,1] = [1+,4,36] A18, [27]+
Dual	?
Properties	convex

E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as HM₈ for an 8-dimensional half measure polytope.

Coxeter named this polytope as 1₅₁ from its Coxeter diagram, with a ring on one of the 1-length branches, and Schläfli symbol ${\displaystyle \left\{3{\begin{array}{l}3,3,3,3,3\\3\end{array}}\right\}}$ or {3,3^5,1}.

Cartesian coordinates

Cartesian coordinates for the vertices of an 8-demicube centered at the origin are alternate halves of the 8-cube:

(±1,±1,±1,±1,±1,±1,±1,±1)

with an odd number of plus signs.

Related polytopes and honeycombs

This polytope is the vertex figure for the uniform tessellation, 2₅₁ with Coxeter-Dynkin diagram:

Images

orthographic projections

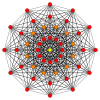
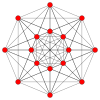
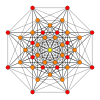
Coxeter plane	B8	D8	D7	D6	D5
Graph
Dihedral symmetry	[16/2]	[14]	[12]	[10]	[8]
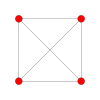
Coxeter plane	D4	D3	A7	A5	A3
Graph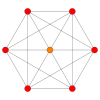
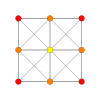Dihedral symmetry	[6]	[4]	[8]	[6]	[4]

References

• H.S.M. Coxeter:
  • Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)

External links

• Olshevsky, George. "Demiocteract". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• Multi-dimensional Glossary

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds