Schwingungslehre

Die Technische Schwingungslehre, auch kurz Schwingungslehre, ist die Wissenschaft von den technischen Schwingungsystemen (Oszillatoren).

Freie Schwingung eines Kragbalkens

Schwingungen spielen in der Natur und Technik eine große Rolle.^[1]:218 Bei schwingfähigen Bauteilen ist deren sichere Auslegung in allen Bereichen der Technik, insbesondere im Maschinenbau, Bauingenieurwesen und in der Elektrotechnik, von großer Bedeutung.^[2]:1 Sie beschäftigt sich mit

• der Analyse von Schwingungssystemen,
• der Einteilung von Schwingungen und
• dem Entstehen von Schwingungen.

Wesentliche Eigenschaften mechanischer Schwingungssysteme sind ihre Steifigkeit und Trägheit, die sie befähigen eine Verformung zurückzustellen, dabei jedoch die Verformungsgeschwindigkeit aufrechtzuhalten. Diese widerstreitenden Eigenschaften führen im sich selbst überlassenen System nach einer irgendwie eingeleiteten, hinreichend kleinen Auslenkung (im linearen Bereich, wo keine Schäden auftreten) wie in der Animation zu Schwingungen. Deren wichtigste Kenngröße ist die Eigenkreisfrequenz, die den Takt der Schwingung vorgibt. Wird das System in diesem Takt, genauer in dieser Frequenz, angeregt, kann es zur Resonanzkatastrophe kommen, die es in technischen Systemen zu vermeiden gilt.

Sie ist eine theoretische Disziplin, die das vollständige Verständnis technischer Schwingungsphänomene anstrebt, dabei auch ihre mathematische Beschreibung nutzt, ohne sie zum Selbstzweck werden zu lassen.^[3]:V Schwingungen werden mit Differentialgleichungen beschrieben, die es aufzustellen, zu interpretieren und zu lösen gilt. Die Lösungen sind in ihrer physikalisch-technischen Bedeutung zu verstehen. Kenntnisse der technischen Schwingungslehre sind in der Entwicklung und Konstruktion unabdingbar.^[2]:VI–1

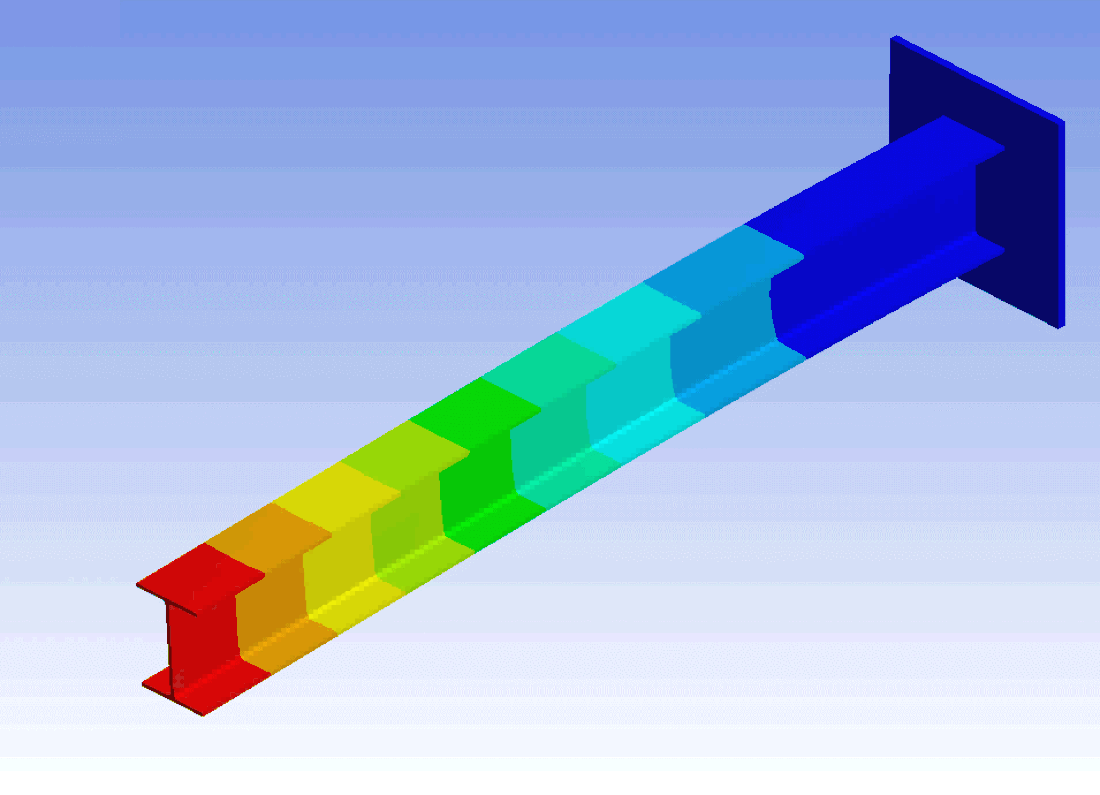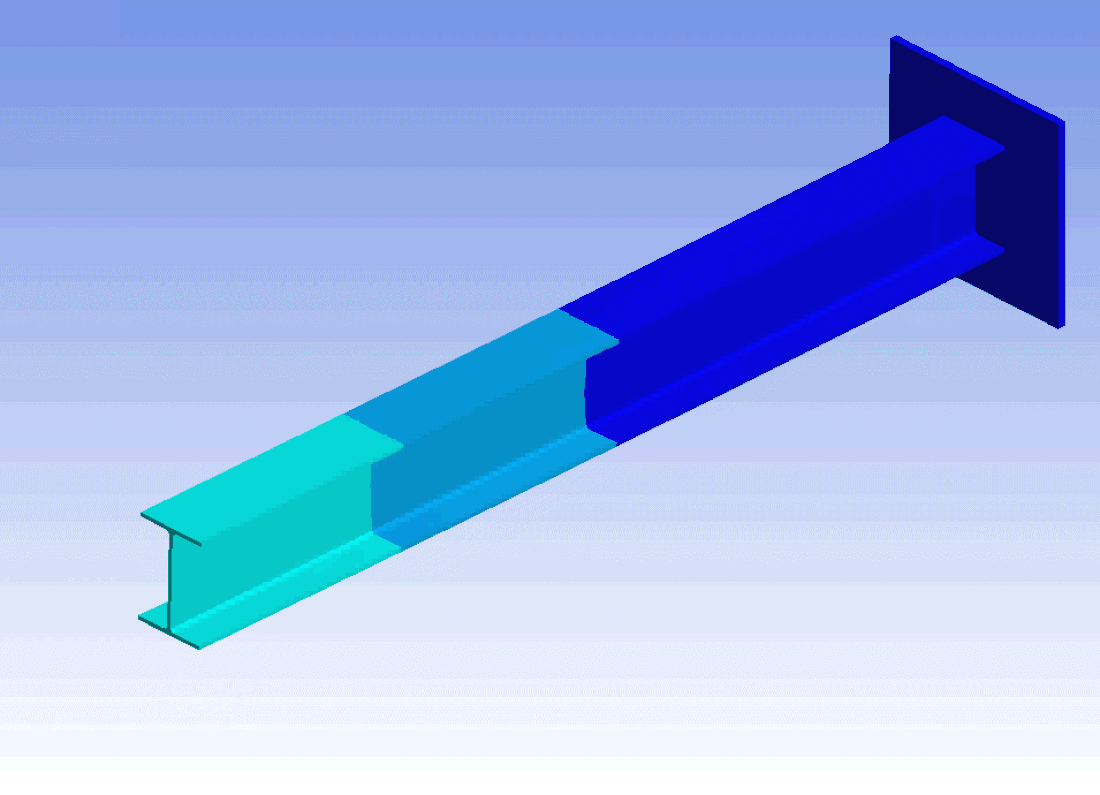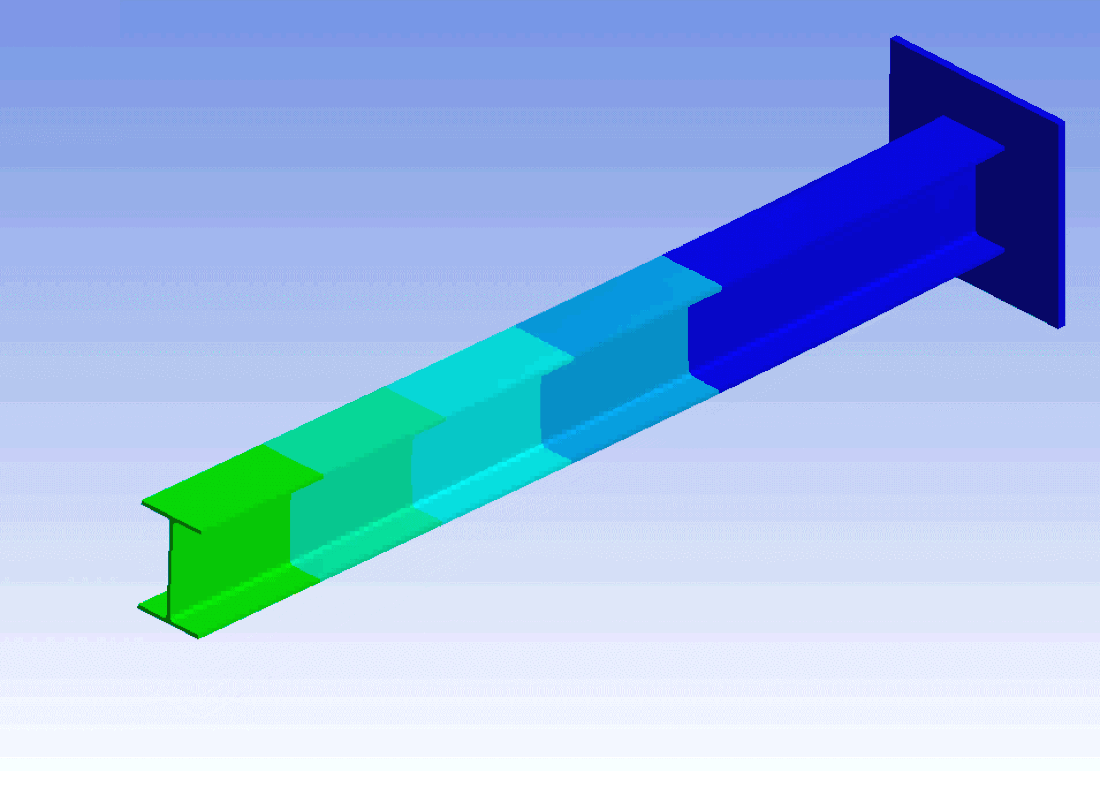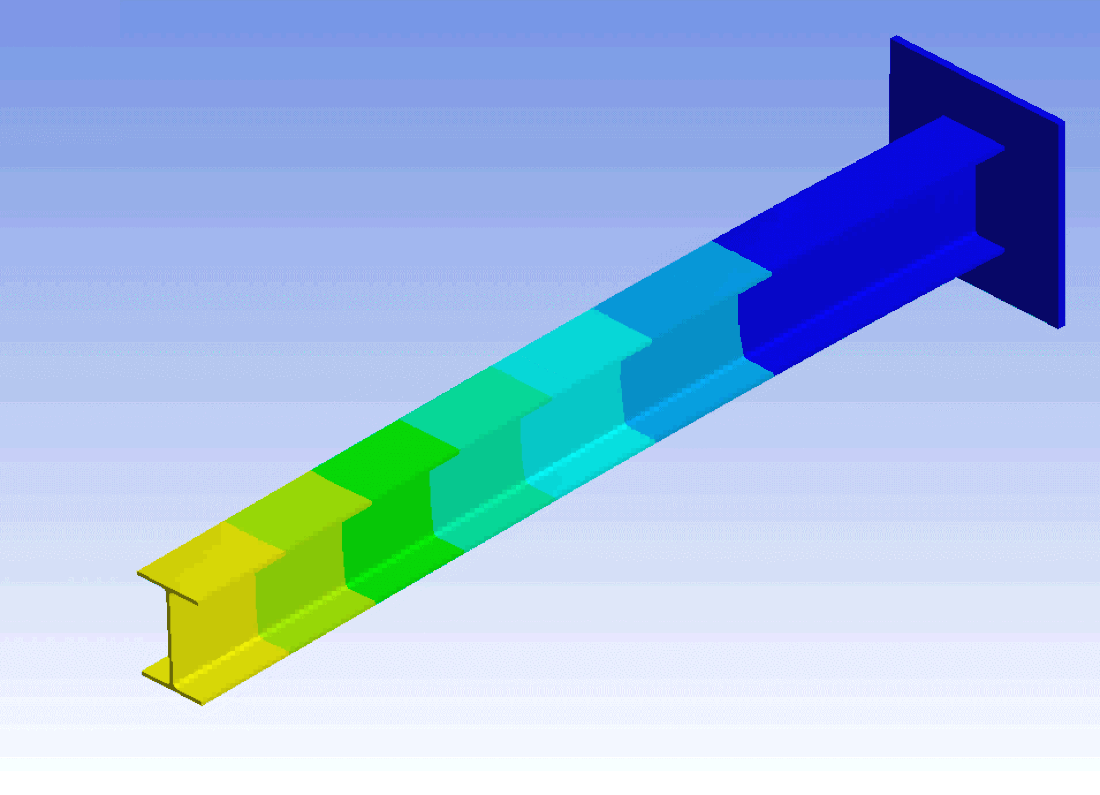
Die Wellenlehre untersucht sich räumlich ausbreitende Schwingungen. In Abgrenzung dazu, befasst sich dieser Artikel mit stationären Schwingungen, wie sie beim Federpendel oder Kragbalken vorkommen, siehe Bild.

Grundsätzliches

Einteilung von Schwingungen und Grundbegriffe

Unter einer Schwingung wird ein sich in gleicher Weise wiederholender Vorgang verstanden, bei dem eine physikalische Größe (wie z. B. der Weg oder die Winkelauslenkung) abwechselnd zu- und abnimmt. Beispiele sind Pendel, Seegang, elektrische Schwingkreise oder Erdbebenwellen.^{[2]:1[1]:219–239} Folgende Begriffe werden häufig benutzt:

Schwinger

Schwingende mechanische Systeme werden auch kurz Schwinger genannt.

Zustandsgröße, Verallgemeinerte Koordinate

Sie ist die interessierende physikalische Größe, wie die Lage eines Partikels, die zeitlichen Schwankungen unterliegt.

Zeitlicher Verlauf

Deterministische sich wiederholende Schwingungen, deren Frequenzanalyse meist die Grundlage der Beurteilung bilden. Aber auch Zufallsschwingungen kommen vor, die beispielsweise vom Wind (siehe Tacoma-Narrows-Brücke#Einsturz der Brücke von 1940) oder von Erdbebenwellen angefacht werden. Mit stochastischer Anregung werden Betriebsschwingformen ermittelt.

Periodische Schwingung

Bei periodischen Schwingungen wiederholt sich der Verlauf mit der Zeit, siehe #Periodische Schwingungen und Funktionen

Entstehung der Schwingung

• Eine autonome Schwingung erfolgt ausschließlich in vom System selbst bestimmten Frequenzen; freie Schwingungen auch als Überlagerung von Eigenschwingungen sind eine Untergruppe. Die in der Einleitung erwähnten Schwingungen sich selbst überlassener Systeme fallen in diese Kategorie. Auch selbsterregte Schwingungen wie beim Pendel sind autonom.
• Bei heteronomen Schwingungen werden die Frequenzen von äußeren Einflüssen verändert. In der Untergruppe der erzwungenen Schwingungen treten zeitlich schwankende Einflüsse wie Kräfte oder Momente auf, die dem System eine Frequenz aufzwingen. In parametererregten Schwingungen ändert sich eine Systemeigenschaft mit der Zeit, sodass Schwingungen angefacht werden. Ein Beispiel ist die Schaukel, bei der die Schwingung durch Streck- und Beugebewegungen buchstäblich aufgeschaukelt wird.

Dämpfung

Sie bewirkt eine Abnahme der Schwingweite in Eigenschwingungen. Bei oszillatorischer Instabilität tritt negative Dämpfung auf, durch die die Schwingung angefacht wird, siehe #Dämpfung technischer Systeme und Stabilitätstheorie.

Zahl der Bewegungs­freiheitsgrade

Sie gibt die Anzahl der notwendigen, voneinander kinematisch unabhängigen Bewegungsmöglichkeiten an, mit denen der Zustand eines Systems eindeutig angegeben wird. Häufig können alle trägheitsbehafteten Systemteile als starr angenommen werden, wodurch diskrete Systeme mit endlich vielen Freiheitsgraden entstehen, was die Analyse vereinfacht.

Bewegungsform

Bei kontinuierlicher Massenbelegung ersetzt die Bewegungsform die Freiheitsgrade. Beim oft benutzten Balken ist die Unterscheidung von Schwingbewegungen

• in Balkenlängsrichtung als Längs- oder Longitudinalschwingung,
• in Querrichtung als Quer- oder Transversalschwingung und
• bei Verwindung als Verdreh- oder Torsionsschwingung

vorteilhaft, siehe #Schwingungen der Kontinua

Schwingungsdifferentialgleichung

Dies ist die Differentialgleichung, die die Schwingung beschreibt, und wird auch kurz Schwingungsgleichung genannt. Im diskreten System sind es Gewöhnliche Differentialgleichungen, im kontinuierlichen Modell Partielle Differentialgleichungen.

Lineare und nichtlineare Schwingungssysteme

• Lineare Systemmodelle sind von großem Vorteil, denn sie lassen sich überlagern und besitzen erregungsunabhängige Systemkenngrößen. Lineare gewöhnliche Differentialgleichungen beschreiben lineare Schwinger. Die Zeitinvarianz der betrachteten Schwinger ist das Ziel der Auslegung.
• Nichtlineare mechanische Schwingungssysteme kennzeichnet Bewegungsdifferentialgleichungen, die allgemeine nichtlineare Abhängigkeiten von Bewegungs- oder Kraftgrößen enthalten. Die Phänomene nichtlinearer Schwingungen sind vielfältig. Es gibt keine Invarianten mehr; beispielsweise kann die „Eigenkreisfrequenz“ von den Anfangsbedingungen abhängen. Häufig führen Linearisierungen am Betriebspunkt zu befriedigenden Ergebnissen.^[2]:2–5

Periodische Schwingungen und Funktionen

Wiedergabe einer Schwingung durch die harmonische Funktion cos.

Siehe auch: Harmonischer Oszillator

Bei periodischen Schwingungen wiederholt sich der Verlauf mit der Zeit (t), und Periodische Funktionen können sie kompakt beschreiben, siehe Animation.^{[2]:7–9[1]:219–221} Die Zeitspanne, bis die Wiederholung auftritt, ist die Periodendauer, Periode oder Schwingungsdauer T, ihr Kehrwert die Frequenz f der Schwingung, das 2π-fache der Frequenz die Kreisfrequenz ω der Schwingung, und die Anzahl der Schwingungen pro Minute ist die Schwingungszahl n.

Die Amplitude ist die maximale Auslenkung, und Schwingungen mit konstanter Amplitude, wie die hier angegebenen, heißen ungedämpft. Schwingungen mit abnehmender Amplitude sind gedämpft und solche mit wachsender Amplitude angefacht. Der Spitze-Tal-Wert entspricht der doppelten Amplitude.

Ein wichtiger Sonderfall periodischer Schwingungen sind die harmonischen Schwingungen wie in der Animation oben, bei denen die Größe mit dem Sinus und Kosinus, sin bzw. cos, in der Zeit t verläuft. Periodische Funktionen können mit (unendlichen) Summen von harmonischen Funktionen dargestellt werden.

Die Summe (Überlagerung) der roten und blauen Kurve ist die immer noch periodische schwarze Kurve (eine Schwebung)

Bei der Überlagerung harmonischer Schwingungen sind zwei Fälle zu unterscheiden:

1. Wenn die beiden Kreisfrequenzen in einem rationalen Verhältnis ω₁/ω₂=p/q mit ganzzahligen sowie teilerfremden p und q stehen, dann ist die sich einstellende Schwingung nicht mehr harmonisch, aber periodisch mit der Periodendauer T=pT₁=qT₂.
2. Wenn die beiden Kreisfrequenzen in keinem rationalen Verhältnis stehen, ist ihre Überlagerung nicht mehr periodisch.

Falls die Frequenzen der beiden Schwingungen nahe beieinander liegen kommt es zu einer Schwebung, wie im Bild.

In Fourierreihen wird eine periodische Schwingung als Überlagerung einer harmonischen Grundschwingung mit ihren Harmonischen dargestellt; hier sind die Kreisfrequenzen ganzzahlige Vielfache der Grundfrequenz. Die Sägezahn- und Rechteckschwingung sind Schwingungen, die eine Überlagerung von unendlich vielen harmonischen Schwingungen sind. Mittels der Fourier-Analysis können Zeitsignale in ihre Frequenzanteile zerlegt werden, und umgekehrt kann aus den Frequenzanteilen das Signal zusammengesetzt werden. In der Mess- und Regelungstechnik ist auch das kontinuierliche Spektrum bedeutsam, das aus der Fourier-Transformation entsteht. Mittels der FFT kann ein zeitdiskretes Signal, wie es bei Messungen anfällt, in seine Frequenzanteile zerlegt und analysiert werden.^[2]:13f

Harmonische Schwingungen können mit dem Zeigermodell in der Animation unten anschaulich dargestellt werden. Ihre allgemeine Bewegungsfunktion ${\displaystyle x}$ als Funktion der Zeit t ist^{[1]:221[2]:9f}

${\displaystyle x(t)=A\sin(\omega t)+B\cos(\omega t)=C\sin(\omega t+\varphi _{0})}$

mit Kreisfrequenz ω, Konstanten ${\displaystyle A=C\cos(\varphi _{0}),B=C\sin(\varphi _{0})}$, Amplitude ${\displaystyle C={\sqrt {A^{2}+B^{2}}}}$ und Nullphasenwinkel φ₀=atan2(B,A). Die Zeitableitungen der Bewegungsfunktion liefern die Geschwindigkeit und die Beschleunigung:

${\displaystyle {\begin{aligned}{\dot {x}}(t)=&\omega \,A\cos(\omega t)-\omega B\,\sin(\omega t)=\omega \,C\cos(\omega t+\varphi _{0})\\{\ddot {x}}(t)=&-\omega ^{2}\,A\sin(\omega t)-\omega ^{2}\,B\cos(\omega t)=-\omega ^{2}\,C\sin(\omega t+\varphi _{0})=-\omega ^{2}\,x(t)\end{aligned}}}$

Hat die Schwingung zu Beginn (bei t=0) die Auslenkung x₀ und die Geschwindigkeit v₀, dann berechnen sich die Konstanten

${\displaystyle A={\frac {v_{0}}{\omega }},\;B=x_{0},\;C={\sqrt {x_{0}^{2}+{\frac {v_{0}^{2}}{\omega ^{2}}}}},\varphi _{0}={\rm {atan2}}\left(x_{0},{\frac {v_{0}}{\omega }}\right)}$

Darstellung mit komplexen Zahlen

Animiertes Zeigermodell

Die mathematische Behandlung wird kürzer und eleganter, wenn komplexe Zahlen mit der imaginären Einheit j²=−1 eingeführt werden. Es ändert sich dadurch nichts an den physikalischen Zusammenhängen,^[4]:469 siehe Animation. Die xy-Ebene wird als Gaußsche Zahlenebene aufgefasst, in der eine komplexe Zahl z=x+jy mit Realteil x und Imaginärteil y einen Punkt darstellt, rot in der Animation. Die reellen Parameter der Zahl beschreiben das beobachtete System: In der Animation stellt der Imaginärteil (die y-Koordinate) die Auslenkung dar, der Realteil (die x-Koordinate) ist zur Geschwindigkeit des Pendelkörpers proportional und der Betrag (r) ist die Amplitude der Schwingung des Federpendels.

Die Polardarstellung der komplexen Zahl ist z=r·e^jφ mit Betrag r=|z| und Argument φ=atan2(y,x), das den Winkel angibt, mit dem die positive x-Achse gegen den Uhrzeigersinn um den Ursprung gedreht werden muss, damit sie durch die Zahl z führt (ein negatives Argument bedeutet eine Drehung im Uhrzeigersinn.) In dieser Darstellung besitzt das Argument dasselbe Vorzeichen wie der Imaginärteil y. An der Stelle z=−r springt das Argument von φ=π nach φ=−π, was der Tatsache entspricht, dass der Hauptwert des komplexen Logarithmus auf der negativen reellen Achse nicht stetig ist. Wird z=r·e^jφ mit einer anderen komplexen Zahl V·e^jζ multipliziert, ergibt das w=V·r·e^j(φ+ζ), d. h. w hat gegenüber z den V-fachen Betrag und ist um den Winkel ζ gegen den Uhrzeigersinn gedreht. Die konjugiert komplexe Zahl w:=V·e^−jζ dreht entsprechend im Uhrzeigersinn. Beispielsweise kann ein #Komplexer Frequenzgang bei harmonischer Erregung elegant in dieser Weise beschrieben werden.

Dämpfung technischer Systeme

Gedämpfter Schwinger

In realen Systemen nehmen die Auslenkungen von freien Schwingungen durch Energie­dissipation mit der Zeit ab bis das System zur Ruhe kommt: Reale Schwingungen sind gedämpft. Als Ursachen kommen in Frage:

Dämpfung durch Schwingungsdämpfer

Diese werden eingebaut, um ein bestimmtes Schwingungsverhalten zu erzielen, z. B. Stoßdämpfer im Fahrwerk. Ziel kann eine Schwingungstilgung oder Resonanzabsorption sein.

Umgebungsdämpfung

Das System bewegt sich in Luft, einem anderen Gas oder in einer Flüssigkeit. Je nachdem, ob das umgebende Medium in Ruhe oder selbst in Bewegung ist, liegt hydrostatische bzw. hydrodynamische Dämpfung vor.

Material- oder Werkstoffdämpfung

Die Dämpfung entsteht z. B. durch quantenmechanische Prozesse in und zwischen den kristallinen Körnern und Phasen eines Materials, Schlupf auf mikroskopischer Ebene oder durch Wachstum von Mikrorissen. Metalle weisen eine geringere Werkstoffdämpfung auf als Kunststoffe.^[5]:197

Lagerdämpfung

In Lagern und Führungselementen tritt häufig Reibung auf. Bei „Trockener Reibung“ ist die Reibkraft konstant; es gibt aber auch geschwindigkeitsproportionale (viskose s. u.) und dem Quadrat der Geschwindigkeit proportionale Lagerdämpfung.

Systemdämpfung

Sie ist abhängig von der konstruktiven Gestalt des Systems. Z. B. hat eine Nietkonstruktion im Allgemeinen eine größere Dämpfung als eine geschweißte Konstruktion.^[2]:87 Zu ihr zählt auch die Fügestellen­dämpfung, die der wahrscheinlich größte Beitrag zur Schwingungsdämpfung realer Maschinen ist.^[5]:197

Dämpfung durch Schallabstrahlung

Schwingende Körper, die von einem Fluid umgeben sind, können Energie durch Schallabstrahlung abgeben, was dämpfend wirkt.^[5]:197

Viskose Dämpfung

Hier ist die Dämpfungskraft proportional zur Geschwindigkeit, ein Ansatz, mit dem lineare Differenzialgleichungen mit wenigen Parametern entstehen, die den mechanischen Energieverlust während der Schwingungen ausdrücken.^[4]:462 Hydraulische Dämpfer weisen sie bei nicht zu großer Geschwindigkeit auf.^{[2]:88[6]:B38}

Rayleigh-, Proportionale- oder α-β-Dämpfung

Es ist ratsam, erzwungene Schwingungen nur in Verbindung mit Dämpfungswerten zu berechnen, da sonst keine brauchbaren Amplitudenwerte in Resonanznähe entstehen. Da oft Dämpfungskonstanten realer Maschinen fehlen, ist es üblich, modale Dämpfungen einzuführen, was am häufigsten mit der Rayleigh-Dämpfung geschieht, die in entsprechend vielen Programmsystemen implementiert ist.^[4]:646 Hier sind die viskosen Dämpfer d

• zum Trägheitskoeffizient m proportional, d=αm, oder
• zum Rückstellkoeffizient k proportional, d=βk.

Der Trägheitskoeffizient ist oft eine Masse und der Rückstellkoeffizient oft eine Federsteifigkeit. Die zur Masse proportionale Dämpfung hat keinen physikalischen Bezug. Die zur Federsteifigkeit proportionale Dämpfung eignet sich zur Modellierung der volumetrischen Werkstoffdämpfung, ist aber für die an der Oberfläche wirkende Schallabstrahlung oder die Fügestellendämpfung physikalisch nicht konsistent.^[5]:196

Strukturelle Dämpfung

Hier ist die Dämpfungskraft proportional zur Auslenkung, was zu einer quadratischen Amplitudenabhängigkeit des Dämpfungsgrads ohne Frequenzabhängigkeit führt.^[5]

Trockene Reibung

Bei Dämpfung durch trockene Reibung (Coulomb’sche Dämpfung) ist die Reibungskraft konstant, aber immer der Geschwindigkeit entgegengesetzt; dies erfordert eine Fallunterscheidung und der Schwinger wird ein nichtlineares System. Die Amplitude der Schwingung nimmt hier linear mit der Zeit ab.

Die Dämpfung kann vernachlässigt werden, wenn nur

• niedere Eigenfrequenzen (und Resonanzgebiete) eines Antriebssystems,
• die Spitzenwerte nach Stoßvorgängen, oder
• Schwingungszustände außerhalb der Resonanzgebiete

interessieren.^[4]:44 Wenn sie doch benötigt wird, kann sie experimentell ermittelt werden aus^[4]:50f

• dem Ausschwingvorgang einer Eigenform (Logarithmisches Dekrement)
• dem Verlustwinkel/der Nacheilung der Schwingungsantwort,
• der Form des #Amplitudengangs in Resonanznähe, oder
• der Hysterese im Kraft-Weg-Diagramm.

Einfache Schwinger

Siehe auch: Harmonischer Oszillator

Das wichtigste System in der technischen Schwingungslehre ist das lineare Feder-Masse-Dämpfer System mit einem Freiheitsgrad, der auch kurz einfacher Schwinger^[1]:222 genannt wird, siehe Bild. Denn zum einen verhalten sich viele Systeme, insbesondere Resonatoren, wie einfache Schwinger (siehe #Einfache Schwinger als Ersatzsystem) und zum anderen lassen sich lineare Systeme, die mehrere (n) Massen enthalten, die mit Federn und Dämpfern aneinander gekoppelt sind, unter bestimmten Voraussetzungen durch Modalanalyse in n entkoppelte einfache Schwinger (Schwingungsmoden) zerlegen.

System aus Feder (k), Masse (m) und Dämpfer (c) mit einem Freiheitsgrad (x)

Der einfache Schwinger im Bild besteht aus einer Masse (m), die in einer Richtung (x) frei verschieblich ist und mit einer Feder (k) und einem Dämpfer (c) gehalten wird.

Nach einer Anfangsauslenkung aus der Ruheposition wirken zwei Kräfte auf die Masse:

• die Federkraft ${\displaystyle F_{k}=k\cdot x}$, die der Auslenkung entgegenwirkt und das Produkt aus Federkonstante k und Auslenkung x ist, und
• die Dämpfungskraft ${\displaystyle F_{d}=d\cdot {\dot {x}}}$, die der Geschwindigkeit entgegenwirkt und bei viskoser Dämpfung das Produkt aus Dämpferkonstante d und Geschwindigkeit ${\displaystyle {\dot {x}}}$ ist (für #Andere Dämpfungsformen siehe dort).

Das zweite newtonsche Gesetz Kraft gleich Masse mal Beschleunigung, F=m·a, angewendet auf die Masse liefert:

${\displaystyle m{\ddot {x}}(t)=-kx(t)-d{\dot {x}}(t)\quad \rightarrow \quad m{\ddot {x}}(t)+d{\dot {x}}(t)+kx(t)=0}$

Hier zeigt sich der Vorteil des Ansatzes mit der geschwindigkeitsproportionalen Dämpfung:^[4]:462

• die entstandene Differentialgleichung ist linear und lässt sich entsprechend leicht lösen,
• es werden nur wenige Parameter gebraucht und
• die dissipative Wirkung der Dämpfung wird erreicht.

Für die schwingungstechnische Form wird die Gleichung durch die Masse dividiert und es entsteht die homogene Schwingungsgleichung:

${\displaystyle {\ddot {x}}(t)+2\delta {\dot {x}}(t)+\omega _{0}^{2}x(t)=0}$

Darin ist^[2]:89

Formelzeichen	Einheit	Name
${\displaystyle \omega _{0}={\sqrt {\frac {k}{m}}}}$	s−1	Eigenkreisfrequenz des ungedämpften Systems (bei d=0)
${\displaystyle \delta ={\frac {d}{2m}}=D\cdot \omega _{0}}$	s−1	Abklingkonstante
${\displaystyle D={\frac {d}{2{\sqrt {mk}}}}=\sin \theta }$	1	Dämpfungsgrad oder Lehr’sches Dämpfungsmaß
θ=arcsin(D)	Radiant	Dämpfungswinkel, der nur bei D≤1 definiert ist, also bei unterkritischer schwacher bis starker Dämpfung.

Bei Krafterregung mittels einer Einzelkraft F(t) oder Fußpunkterregung^[2]:153 über den auf und ab schwingenden Boden, bei der die x-Koordinate des Bodens x_F(t) vorgegeben wird, liefert Newtons Gesetz

${\displaystyle m{\ddot {x}}(t)=F(t)-k[x(t)-x_{F}(t)]-d[{\dot {x}}(t)-{\dot {x}}_{F}(t)]}$

Division durch die Masse ergibt nach Umstellung die inhomogene Schwingungsgleichung^[2]:154

${\displaystyle {\ddot {x}}(t)+2\delta {\dot {x}}(t)+\omega _{0}^{2}x(t)={\frac {F(t)}{m}}+\omega _{0}^{2}x_{F}(t)+2\delta {\dot {x}}_{F}(t)}$

In Abwesenheit von Krafterregung ${\displaystyle F(t)}$, Federfußpunkterregung ${\displaystyle x_{F}}$ oder Dämpferfußpunkterregung ${\displaystyle {\dot {x}}_{F}}$, tritt der entsprechende Term auf der rechten Seite nicht auf und ist wegzulassen.

Einfache Schwinger als Ersatzsystem

In der Technik kommen schwingfähige Systeme vor, in denen die Rückstellkraft nicht von einer Feder oder die Trägheit nicht (nur) von einer Masse herrührt. Dann kann der Schwinger als Ersatzsystem dienen, in dem entsprechende Ersatzfedersteifigkeiten k_ers und Ersatzmassen m_ers eingesetzt werden. Gelegentlich wird auch die Verschiebung x durch eine verallgemeinerte Koordinate q ersetzt.^[2]:139f Die Tabelle zeigt Beispiele hierfür.^[2]:231ff

Schwinger	Verallgemeinerte Koordinate	Ersatzmasse	Ersatzsteifigkeit
mathematisches Pendel	Drehwinkel φ	Masse m	g/l[1]:225
physikalisches Pendel	Drehwinkel φ	Masse m	mgl/J[1]:226
Drehschwinger	Drehwinkel	Massen­trägheits­moment	Drehfeder­steifigkeit
Rollschwinger[7]	Auslenkung	m+J/r2	Feder­steifigkeit
Torsionspendel	Drehwinkel φ	Massen­trägheits­moment J des Pendelkörpers	Direktionsmoment
Wasserpendel	Auslenkung y	Masse der gesamten Wassersäule	2·ρ·A·g
Reibschwinger	Auslenkung	Masse	μ·mg/b, b=Halber Abstand der Rollen
Kragbalken mit Einzelmasse am Ende	Axiale Verschiebung	Masse des Pendelkörpers	kers=EA/l
Kragbalken mit Einzelmasse am Ende	Durchbiegung		kers=3EI/l3, l=Länge des Balkens
Träger auf zwei Stützen mit mittiger Einzelmasse			kers=48EI/l3, l=Länge des Balkens
Beidseitig fest eingespannter Träger mit mittiger Einzelmasse			kers=192EI/l3, l=Länge des Balkens

Schaltung von Federn

Die im vorangegangenen Abschnitt genannten Schwinger können in realen Systemen in mannigfacher Weise kombiniert auftreten. Dabei gilt:^{[6]:B37[1]:231}

• Werden Federn parallel geschaltet, addieren sich ihre Steifigkeiten zur Ersatzsteifigkeit ${\displaystyle \textstyle k_{\text{ers}}=\sum _{i}k_{i}}$.
• Bei Reihen- oder Hintereinanderschaltung addieren sich ihre Kehrwerte, die auch Nachgiebigkeiten h genannt werden, zur Ersatznachgiebigkeit ${\displaystyle \textstyle h_{\text{ers}}:={\frac {1}{k_{\text{ers}}}}=\sum _{i}{\frac {1}{k_{i}}}:=\sum _{i}h_{i}}$.

Massebehaftete Feder

Siehe auch: Federpendel

Wenn gegenüber der Masse des schwingenden Körpers die Federmasse nicht vernachlässigt werden darf, kann sie näherungsweise berücksichtigt werden. Unter der Annahme, dass die Verschiebungen denen bei statischer Auslenkung gleich sind, kann die kinetische Energie der Feder als Funktion der Geschwindigkeit v des schwingenden Körpers berechnet werden:

${\displaystyle E_{\text{kin,F}}={\frac {1}{3}}{\frac {m_{F}}{2}}v^{2}}$

d. h. ein Drittel der Federmasse trägt zur kinetischen Energie des Schwingers bei. In die Gesamtenergie des Schwingers geht nun die kinetische Energie der Einzelmasse plus einem drittel der Federmasse ein; diese ist demnach als (Ersatz-)Masse des Systems anzusetzen: m_ers=m+κ·m_F mit κ=¹⁄₃.^[2]:33 Bei der Biegung des Kragbalkens ist κ=³³⁄₁₄₀ und beim beidseitig aufliegenden durchbiegenden Balken mit mittiger Masse ist κ=¹⁷⁄₃₅.^[6]:B37

Sich selbst überlassene Schwinger

→ Hauptartikel: Schwingung#Linear gedämpfte Schwingung und Harmonischer Oszillator#Lineare Dämpfung

Der sich selbst überlassene Schwinger oszilliert mit einer eingeprägten Amplitude aber in einer ihm eigenen Geschwindigkeit, die von seiner Eigenkreisfrequenz bestimmt wird.

Um diese zu ermitteln, wird der Ansatz

${\displaystyle x(t)=A\cdot e^{\lambda t}\;\rightarrow \;{\dot {x}}(t)=\lambda A\cdot e^{\lambda t}\;\rightarrow \;{\ddot {x}}(t)=\lambda ^{2}A\cdot e^{\lambda t}}$

mit Amplitude A, e-Funktion e^···, Exponent λ und Zeit t in die #homogene Schwingungsgleichung (Bezeichnungen siehe dort) ${\displaystyle {\ddot {x}}(t)+2\delta {\dot {x}}(t)+\omega _{0}^{2}x(t)=0}$ eingesetzt mit dem Ergebnis:^[1]:240

${\displaystyle (\lambda ^{2}+2\delta \lambda +\omega _{0}^{2})Ae^{\lambda t}=0\quad \rightarrow \quad \lambda _{1,2}=-\delta \pm {\sqrt {\delta ^{2}-\omega _{0}^{2}}}}$

Vier Fälle sind zu unterscheiden:

• keine Dämpfung entsprechend δ=0 und D=0,
• schwache bis starke Dämpfung 0 < δ < ω₀ entsprechend 0 < D < 1,
• kritische Dämpfung δ = ω₀ entsprechend D = 1, und
• sehr starke Dämpfung^[8] δ > ω₀ entsprechend D > 1.

Nur bei kritischer bis sehr starker Dämpfung ist der Exponent λ eine reelle Zahl, und die Bewegungsfunktion hat im Wesentlichen einen exponentiell abklingenden Verlauf. Im nicht bis stark gedämpften Schwinger ist λ eine komplexe Zahl und die eulersche Formel führt auf die Wellenfunktionen Sinus und Cosinus, die bei vorhandener Dämpfung eine abnehmende Amplitude besitzen.

Die Tabelle gibt die Bewegungsfunktionen in den vier Fällen und die zugehörigen Parameter für eine Anfangsauslenkung x₀ und eine Anfangsgeschwindigkeit v₀ zur Zeit t=0.

Däm­pfungs­grad D	Bewegungsfunktion	Parameter
Ohne Dämpfung D=0[2]:32	${\displaystyle {\begin{aligned}x(t)=&A\cos(\omega _{0}t)+B\sin(\omega _{0}t)\\=&C\sin(\omega _{0}t+\varphi _{0})\end{aligned}}}$	${\displaystyle {\begin{aligned}A=&x_{0},\quad B={\frac {v_{0}}{\omega _{0}}}\\C=&{\sqrt {x_{0}^{2}+\left({\frac {v_{0}}{\omega _{0}}}\right)^{2}}}\\\varphi _{0}=&{\rm {atan2}}(x_{0}\omega _{0},v_{0})\end{aligned}}}$
Schwache bis starke Dämpfung[8] D<1[2]:91f	${\displaystyle {\begin{aligned}x(t)=&e^{-\delta t}{\big [}A\cos(\omega _{d}t)+B\sin(\omega _{d}t){\big ]}\\=&Ce^{-\delta t}\sin(\omega _{d}t+\varphi _{0})\\\omega _{d}=&\omega _{0}{\sqrt {1-D^{2}}},\quad \delta =\omega _{0}D\end{aligned}}}$	${\displaystyle {\begin{aligned}A=&x_{0},\quad B={\frac {v_{0}+\delta x_{0}}{\omega _{d}}}\\C=&{\sqrt {x_{0}^{2}+\left({\frac {v_{0}+\delta x_{0}}{\omega _{d}}}\right)^{2}}}\\\varphi _{0}=&{\rm {atan2}}(x_{0}\omega _{d},v_{0}+\delta x_{0})\end{aligned}}}$
Kritische Dämpfung D=1[2]:98	${\displaystyle x(t)=e^{-\delta t}(A+Bt),\quad \delta =\omega _{0}}$	${\displaystyle A=x_{0},\quad B=v_{0}+\delta x_{0}}$
Sehr starke Dämpfung[8] D>1[2]:96	${\displaystyle {\begin{aligned}x(t)=&e^{-\delta t}\left(Ae^{\kappa t}+Be^{-\kappa t}\right)\\\kappa =&\omega _{0}{\sqrt {D^{2}-1}}<\delta \end{aligned}}}$	${\displaystyle {\begin{aligned}A=&{\frac {v_{0}+(\delta +\kappa )x_{0}}{2\kappa }}\\B=&-{\frac {v_{0}+(\delta -\kappa )x_{0}}{2\kappa }}\end{aligned}}}$

Bewegungsfunktion y(t) des viscos gedämpften Schwingers

Im wichtigen Sonderfall der schwach bis stark gedämpften Schwingung (0 < D < 1) stellt sich eine quasiperiodische oder quasiharmonische Schwingung ein, deren Quasi-Periodendauer

${\displaystyle T_{d}:={\frac {2\pi }{\omega _{d}}}}$

(T im Bild) oft ungenau „Schwingungsdauer des gedämpften Systems“ genannt wird. Die Schwingung besitzt die Einhüllende ${\displaystyle \pm Ae^{-\delta t}}$ (blau im Bild) und das Verhältnis der Auslenkungen zu zwei Zeitpunkten im Abstand T_d

${\displaystyle \Lambda =\ln \left({\tfrac {x(t)}{x(t+T_{d})}}\right)=\delta T_{d}}$

wird Logarithmisches Dekrement genannt, das konstant ist: Die Schwingungsamplitude nimmt exponentiell mit der Zeit ab.

Einige Beziehungen zwischen den Kenngrößen der schwach gedämpften Schwingung sind in der Tabelle angegeben.

	δ	θ	Λ	m,d,k
D=	${\displaystyle {\frac {\delta }{\omega _{0}}}}$	${\displaystyle \sin(\theta )}$	${\displaystyle {\frac {\frac {\Lambda }{2\pi }}{\sqrt {1+\left({\frac {\Lambda }{2\pi }}\right)^{2}}}}}$	${\displaystyle {\frac {d}{2{\sqrt {km}}}}}$
ωd=	${\displaystyle {\sqrt {\omega _{0}^{2}-\delta ^{2}}}}$	${\displaystyle \omega _{0}\cos(\theta )}$	${\displaystyle {\frac {\omega _{0}}{\sqrt {1+\left({\frac {\Lambda }{2\pi }}\right)^{2}}}}}$	${\displaystyle {\sqrt {{\frac {k}{m}}-\left({\frac {d}{2m}}\right)^{2}}}}$

Andere Dämpfungsformen

Bewegungsfunktion bei trockener Reibung

Bei Dämpfung durch trockene Reibung (Coulomb’sche Dämpfung)^{[2]:106ff[1]:236f} ist die Reibungskraft R konstant, aber immer der Geschwindigkeit entgegengesetzt. Es müssen zwei Fälle unterschieden werden, wodurch das System nicht mehr linear ist und mit keiner analytischen Funktion darstellbar ist. Bei fehlender äußerer Erregung ergibt sich die #inhomogene Schwingungsgleichung

${\displaystyle {\ddot {x}}(t)+\omega _{0}^{2}x(t)={\begin{cases}-{\frac {R}{m}}&{\text{falls}}\;{\dot {x}}(t)>0\\{\frac {R}{m}}&{\text{falls}}\;{\dot {x}}(t)<0\end{cases}}}$

ohne geschwindigkeitsproportionale Dämpfung (δ=0) aber mit Krafterregung (F=±R). Die Lösung erfordert ebenfalls Fallunterscheidungen:

${\displaystyle x(t)={\begin{cases}C_{1}\cos(\omega _{0}t)+C_{2}\sin(\omega _{0}t)-{\frac {R}{k}}&{\text{falls}}\;{\dot {x}}(t)>0\\D_{1}\cos(\omega _{0}t)+D_{2}\sin(\omega _{0}t)+{\frac {R}{k}}&{\text{falls}}\;{\dot {x}}(t)<0\end{cases}}}$

Die Konstanten C_1,2 und D_1,2 müssen an die Anfangsbedingungen und die Übergangsbedingungen in den Umkehrpunkten nach jeder Halbschwingung angepasst werden. Bei jeder Halbschwingung nimmt die Amplitude um 2R/k – also linear mit der Zeit – ab, und spätestens^[9] wenn die Amplitude R/k unterschreitet, tritt im Umkehrpunkt Haftreibung ein und bleibt die Masse dort stehen.

Fremderregte Schwinger

Siehe auch: Erzwungene Schwingung

Die Partikularlösung ${\displaystyle x_{p}(t)}$ für die #inhomogene Schwingungsgleichung befriedigt ${\displaystyle {\ddot {x}}_{p}(t)+2\delta {\dot {x}}_{p}(t)+\omega _{0}^{2}x_{p}(t)=a(t)}$ mit vorgegebenem Beschleunigungsverlauf 𝛼(t). Wegen der Linearität der Differentialgleichung können zur Partikularlösung Lösungen der homogenen Schwingungsgleichung beliebig superponiert werden, beispielsweise um Anfangsbedingungen einzuhalten.

Bei vorhandener Dämpfung (praktisch immer) nimmt der homogene Lösungsanteil mit der Zeit immer mehr ab und es dominiert der durch eine Erregerkraft aufgeprägte partikuläre Anteil. Dann ist der Einschwingvorgang beendet.^[1]:254

Im Folgenden wird das eingeschwungene System vorausgesetzt.

Komplexer Frequenzgang bei harmonischer Erregung

In der Technik werden harmonische Erregungen beispielsweise durch gleichförmig rotierende Massen eingebracht, die eine Unwucht besitzen. Im eingeschwungenen Zustand bewegt sich dann der Schwinger im Takt der Erregung mit nacheilender Antwort. Bei sehr langsamer Erregung vermag der Schwinger der Erregung zu folgen; er folgt nahezu in Phase. Im Resonanzfall eilt die Antwort um 90° oder ^π⁄₂ nach und die Amplitude ist maximal. Reale Systeme gehen hier leicht kaputt, was als Resonanzkatastrophe bekannt ist, oder werden verstimmt, weil sich ihre Federkonstante ändert. Ferner ist in realen Systemen immer Dämpfung vorhanden. Alles zusammengenommen bewirkt, dass die Amplituden in realen Systemen oft begrenzt bleiben. Von Ausnahmefällen abgesehen (Schwingförderer und Siebmaschinen werden oft im Resonanzbetrieb gefahren) ist der Resonanzfall in technischen Systemen zu vermeiden.^[2]:123 Bei weiter ansteigender Erregerfrequenz vermag der Schwinger der Erregung immer weniger zu folgen, die Amplitude nimmt ab, aber die Nacheilung wird größer bis der Schwinger in Gegenphase ist, d. h. entgegen der Erregung schwingt.

Dieses Verhalten kann elegant in der #Darstellung mit komplexen Zahlen nachgewiesen werden.^[2]:140 Dazu wird die Erregung in der Form ${\displaystyle F(t)={\hat {F}}e^{{\rm {j}}\Omega t}}$ mit Amplitude ${\displaystyle {\hat {F}}}$ sowie Erregerkreisfrequenz Ω und der Ansatz ${\displaystyle x(t)={\hat {x}}e^{{\rm {j}}\Omega t}}$ mit Amplitude ${\displaystyle {\hat {x}}}$ in die #inhomogene Schwingungsgleichung eingesetzt:^[1]:254

${\displaystyle {\ddot {x}}(t)+2\delta {\dot {x}}(t)+\omega _{0}^{2}x(t)=(-\Omega ^{2}+2\delta {\rm {j}}\Omega +\omega _{0}^{2}){\hat {x}}e^{{\rm {j}}\Omega t}={\frac {\hat {F}}{m}}e^{{\rm {j}}\Omega t}=:\omega _{0}^{2}x_{0}Ee^{{\rm {j}}\Omega t},\quad {\hat {F}}:=kEx_{0}}$

Der Faktor E berücksichtigt die Art der Erregung:^[1]:254

E	Erregung
${\displaystyle 1}$	Krafterregung oder Erregung über eine Feder
${\displaystyle 2D\eta }$	Erregung über einen Dämpfer mit Dämpfungsgrad D
${\displaystyle \eta ^{2}}$	Erregung durch eine rotierende Unwucht

Division durch die Exponentialfunktion liefert mit η=Ω/ω₀ und umgestellt:

${\displaystyle {\hat {x}}={\frac {1}{-\Omega ^{2}+2\delta {\rm {j}}\Omega +\omega _{0}^{2}}}{\frac {\hat {F}}{m}}={\frac {E}{-\eta ^{2}+2{\rm {j}}D\eta +1}}x_{0}}$

Der Bruch ist der komplexe Frequenzgang und seine Polardarstellung lautet

${\displaystyle H({\rm {j}}\eta ):={\frac {E}{-\eta ^{2}+2{\rm {j}}D\eta +1}}=:V(\eta )\,e^{-{\rm {j}}\zeta (\eta )}}$

Die Schwingungsantwort ${\displaystyle {\hat {x}}}$ wird demnach betraglich um den Faktor V(η) skaliert und ist um den Winkel ζ(η) im Uhrzeigersinn phasenverschoben.^{[2]:142[1]:254} Die dimensionslose Vergrößerungsfunktion

${\displaystyle V(\eta )={\frac {E}{\sqrt {(1-\eta ^{2})^{2}+(2D\eta )^{2}}}}={\frac {E\omega _{0}^{2}}{\sqrt {(\Omega ^{2}-\omega _{0}^{2})^{2}+4\delta ^{2}\Omega ^{2}}}}}$

wird auch Amplituden-Frequenzgang oder kurz Amplitudengang genannt. Die Bilder stellen die Vergrößerungsfunktionen in den drei Fällen graphisch dar.

• 
  Amplitudengang bei Krafterregung
• 
  Amplitudengang bei Dämpferfusspunkterregung
• 
  Amplitudengang bei Unwuchterregung

Außer bei Erregung mit einem Dämpfer wächst der Amplitudengang im ungedämpften Fall (D=0) in der Eigenkreisfrequenz entsprechend η=1 über alle Grenzen, was, wie oben bereits begründet, unphysikalisch ist. Die stationären Punkte des Amplitudengangs in den drei Erregungsarten sind in der Tabelle aufgeführt.

E	Stationärer Punkt	Vergrößerungsfunktion
${\displaystyle 1}$	${\displaystyle \eta _{1}=0}$	${\displaystyle V_{1}(\eta _{1})=1}$
	${\displaystyle 0<D\leq {\frac {\sqrt {2}}{2}}\;\rightarrow \;\eta _{2}={\sqrt {1-2D^{2}}}}$	${\displaystyle V_{1}(\eta _{2})={\frac {1}{2D{\sqrt {1-D^{2}}}}}}$
${\displaystyle 2D\eta }$	${\displaystyle \eta _{3}=1}$	${\displaystyle V_{2}(\eta _{3})=1}$
${\displaystyle \eta ^{2}}$	${\displaystyle \eta _{4}=0}$	${\displaystyle V_{3}(\eta _{4})=0}$
	${\displaystyle 0<D<{\frac {\sqrt {2}}{2}}\;\rightarrow \;\eta _{5}={\frac {1}{\sqrt {1-2D^{2}}}}}$	${\displaystyle V_{3}(\eta _{5})={\frac {1}{2D{\sqrt {1-D^{2}}}}}}$

Phasengang bei harmonischer Erregung eines gedämpften Systems

Der Phasenfrequenzgang oder kurz Phasengang

${\displaystyle \zeta (\eta )={\rm {atan2}}(2D\eta ,1-\eta ^{2})>0}$

ist gleich der negativen Argumentfunktion des komplexen Frequenzgangs und in den drei Erregungsarten identisch. Die Phase dreht immer im Uhrzeigersinn, sodass die Antwort der Erregung jedenfalls nacheilt. Die Tabelle enthält einige wichtige Werte.

η	0	1	${\displaystyle {\sqrt {1-2D^{2}}}}$	${\displaystyle {\frac {1}{\sqrt {1-2D^{2}}}}}$	∞
φ(η)	0	π⁄2	${\displaystyle \arccos \left({\frac {D}{\sqrt {1-D^{2}}}}\right)}$	${\displaystyle \pi -\arccos \left({\frac {D}{\sqrt {1-D^{2}}}}\right)}$	π

Darin ist arccos die Umkehrfunktion des Cosinus.

Periodische Erregung

Jede periodische Funktion kann durch eine Fourier-Reihe dargestellt werden, die aus der Grundschwingung und ihren Harmonischen besteht. Der Schwinger antwortet dann auf jedes Glied der Reihe gemäß dem Amplituden- und Phasengang aus Abschnitt #Komplexer Frequenzgang bei harmonischer Erregung. Für praktische Anwendungen genügen bereits einige Reihenglieder, für eine gute Wiedergabe der Schwingungsantwort.^[2]:122

Beliebige Erregung

Betrachtet wird der ungedämpfte Fall, in dem die #inhomogene Schwingungsgleichung

${\displaystyle {\ddot {x}}(t)+\omega _{0}^{2}x(t)={\frac {F(t)}{m}}}$

lautet, wo auf der rechten Seite eine anregende Kraft steht. Ist eine Parikularlösung gefunden, die diese Gleichung erfüllt, können zwecks Einhaltung der Anfangsbedingungen Bewegungsfunktionen addiert werden, die die #homogene Schwingungsgleichung mit einer Null auf der rechten Seite befriedigen. Die Parikularlösung ergibt sich hier aus dem Faltungsintegral^[2]:115f

${\displaystyle x_{p}(t)={\frac {1}{m\omega _{0}}}\int _{0}^{t}F(\tau )\sin {\big (}\omega _{0}(t-\tau ){\big )}\,{\rm {d}}\tau }$

Denn die Kraft ist die Zeitableitung des Impulses p=m·v:

${\displaystyle F={\frac {{\rm {d}}p}{{\rm {d}}t}}=m{\frac {{\rm {d}}v}{{\rm {d}}t}}\quad \rightarrow \quad {\rm {d}}v={\frac {F}{m}}{\rm {d}}t}$

Die Bewegungsfunktion des homogenen Systems infolge der Anfangsbedingung x(t₀)=0 und v(t₀)=v₀ ist

${\displaystyle x(t)={\frac {v_{0}}{\omega _{0}}}\sin {\big (}\omega _{0}(t-t_{0}){\big )}}$

Das Geschwindigkeitsinkrement ${\displaystyle {\rm {d}}v}$ aufgrund des Kraftstoßes als „Anfangsgeschwindigkeit“ zur Zeit t₀=τ eingesetzt, ergibt

${\displaystyle {\rm {d}}x={\frac {F(\tau ){\rm {d}}\tau }{m\omega _{0}}}\sin {\big (}\omega _{0}(t-\tau ){\big )},\;t>\tau }$

Die Bewegungsfunktion ${\displaystyle \textstyle x_{p}=\int _{0}^{t}{\rm {d}}x}$ infolge des Kraftverlaufs ergibt sich aus dem oben angegebenen Integral. Siehe auch Lineare gewöhnliche Differentialgleichung#Spezielle Verfahren zum Auffinden einer partikulären Lösung.

Schwingung diskreter Systeme mit endlich vielen Freiheitsgraden

Maschinen und deren Baugruppen lassen sich durch die Modellierung als Mehrkörpersystem oder die Finite-Elemente-Methode auf ein lineares Berechnungsmodell reduzieren. Oft reichen Berechnungsmodelle mit wenigen Freiheitsgraden aus, aber es werden auch Berechnungsmodelle mit Millionen Freiheitsgraden benutzt. Mit der Anzahl der Freiheitsgrade steigt in jedem Fall der Rechenaufwand, aber nicht immer die Genauigkeit der Ergebnisse, die von der Güte der Eingabedaten und davon abhängt, ob die wesentlichen Einflussgrößen richtig erfasst werden. Man kann mit einem Modell mit wenigen Freiheitsgraden das reale Verhalten oft schon hinreichend genau beschreiben.^[4]:371

Die wesentlichen Methoden und Analysen von Systemen mit mehreren Freiheitsgraden lassen sich übersichtlich am System mit zwei Freiheitsgraden aufzeigen. Für mehrere Freiheitsgrade ist die Darstellung in Matrix-Schreibweise unverzichtbar.^[2]:161ff.

Zwei-Massen-Schwinger

Prinzipmodell eines Zwei-Massen-Schwingers.

Beim Zwei-Massen-Schwinger im Bild sind zwei Massen m_1,2 mit je einer Feder k_1,3 und einem Dämpfer c_1,3 an festen Wänden und mit einer Feder k₂ und einem Dämpfer c₂ aneinander gekoppelt. Jede Masse hat einen eigenen Freiheitsgrad x_1,2, weswegen das System auch mit zwei gekoppelten Schwingungsgleichungen beschrieben wird, die wie beim einfachen Schwinger aus Newtons zweitem Gesetz folgen:^[2]:187ff

${\displaystyle {\begin{aligned}m_{1}{\ddot {x}}_{1}=&F_{1}+d_{2}({\dot {x}}_{2}-{\dot {x}}_{1})-d_{1}{\dot {x}}_{1}+k_{2}(x_{2}-x_{1})-k_{1}x_{1}\\m_{2}{\ddot {x}}_{2}=&F_{2}-d_{2}({\dot {x}}_{2}-{\dot {x}}_{1})-d_{3}{\dot {x}}_{2}-k_{2}(x_{2}-x_{1})-k_{3}x_{2}\end{aligned}}}$

mit zwei im Bild nicht dargestellten Erregerkräften F_1,2 an den Massen m_1,2 und Dämpfungskonstanten d_1,2,3 der Dämpfer c_1,2,3. Umgestellt ergibt sich

${\displaystyle {\begin{aligned}m_{1}{\ddot {x}}_{1}+(d_{1}+d_{2}){\dot {x}}_{1}-d_{2}{\dot {x}}_{2}+(k_{1}+k_{2})x_{1}-k_{2}x_{2}=&F_{1}\\m_{2}{\ddot {x}}_{2}+(d_{3}+d_{2}){\dot {x}}_{2}-d_{2}{\dot {x}}_{1}+(k_{3}+k_{2})x_{2}-k_{2}x_{1}=&F_{2}\end{aligned}}}$

Mit den Matrizen^[2]:193

Massenmatrix	${\displaystyle \mathbf {M} ={\begin{pmatrix}m_{1}&\\&m_{2}\end{pmatrix}}}$	Lösungsvektor	${\displaystyle {\vec {x}}={\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}}$
Steifigkeitsmatrix	${\displaystyle \mathbf {K} ={\begin{pmatrix}k_{1}+k_{2}&-k_{2}\\-k_{2}&k_{3}+k_{2}\end{pmatrix}}}$	Erregerkraft	${\displaystyle {\vec {F}}={\begin{pmatrix}F_{1}\\F_{2}\end{pmatrix}}}$
Dämpfungsmatrix	${\displaystyle \mathbf {D} ={\begin{pmatrix}d_{1}+d_{2}&-d_{2}\\-d_{2}&d_{3}+d_{2}\end{pmatrix}}\;}$

schreibt sich das kompakt als Matrizendifferentialgleichung

${\displaystyle \mathbf {M} {\ddot {\vec {x}}}+\mathbf {D} {\dot {\vec {x}}}+\mathbf {K} {\vec {x}}={\vec {F}}}$

Hier ist die Massenmatrix eine Diagonalmatrix und die Steifigkeitsmatrix voll besetzt, was bei Federkopplung der Fall ist. Bei Massenkopplung hat die Steifigkeitsmatrix Diagonalgestalt und die Massenmatrix besitzt Nebendiagonalglieder.^[2]:167 Kreiselwirkungen, wie sie bei rotierenden Wellen auftreten, bringen schiefsymmetrische Anteile in die Dämpfungsmatrix D ein; eine rein antisymmetrische Dämpfungsmatrix bewirkt daher keine Dämpfung.^[4]:464 Unter den Voraussetzungen für den Satz von Betti sind die Massen- und Steifigkeitsmatrizen – wie hier – symmetrisch, wovon im Folgenden auch ausgegangen wird.

Mit dem Ansatz ${\displaystyle {\vec {x}}=e^{\lambda t}{\vec {u}}}$ mit konstantem Amplitudenvektor ${\displaystyle {\vec {u}}}$ entsteht in Abwesenheit von Erregerkräften das Problem

${\displaystyle (\lambda ^{2}\mathbf {M} +\lambda \mathbf {D} +\mathbf {K} ){\vec {u}}={\vec {0}}}$

Bei #Rayleigh-Dämpfung ist D=αM+βK und es entsteht nach

${\displaystyle [\lambda ^{2}\mathbf {M} +\lambda (\alpha \mathbf {M} +\beta \mathbf {K} )+\mathbf {K} ]{\vec {u}}={\vec {0}}\;\rightarrow \;(\mathbf {K} +\eta \mathbf {M} ){\vec {u}}={\vec {0}},\;\eta ={\frac {\lambda (\lambda +\alpha )}{1+\beta \lambda }}}$

ein verallgemeinertes Eigenwertproblem. Dessen Spektralzerlegung liefert die Eigenwerte η und Eigenvektoren des Systems. Wegen der Symmetrie der Matrizen sind die Eigenwerte und -vektoren reell, aber die Werte

${\displaystyle \lambda _{1,2}={\frac {-\alpha -\beta \eta \pm {\sqrt {(\alpha +\beta \eta )^{2}-4\eta }}}{2}}}$

können komplex sein.

Bei einer Erregerkraft ${\displaystyle {\vec {F}}={\vec {f}}e^{{\rm {j}}\Omega t}}$ mit konstantem Kraftamplitudenvektor ${\displaystyle {\vec {f}}}$ wird der Ansatz ${\displaystyle {\vec {x}}=e^{{\rm {j}}\Omega t}{\vec {u}}}$ eingesetzt mit der Konsequenz (j²=−1):^[4]:470

${\displaystyle (-\Omega ^{2}\mathbf {M} +{\rm {j}}\Omega \mathbf {D} +\mathbf {K} ){\vec {u}}={\vec {f}}}$

Daraus berechnet sich die komplexe Amplitude

${\displaystyle {\vec {u}}=\mathbf {H} ({\rm {j}}\Omega ){\vec {f}},\quad \mathbf {H} ({\rm {j}}\Omega ):=(-\Omega ^{2}\mathbf {M} +{\rm {j}}\Omega \mathbf {D} +\mathbf {K} )^{-1}}$

Hier ist H die komplexe Frequenzgangs­matrix, die die Inverse Matrix des rechten Klammerausdrucks ist, vgl. #Komplexer Frequenzgang bei harmonischer Erregung des einfachen Schwingers. Sie gibt zu einem komplexen Erregerkraftvektor ${\displaystyle {\vec {f}}}$ die komplexe Antwort ${\displaystyle {\vec {u}}}$, der eine (reelle) Amplitude und ein Phasenwinkel gegenüber der Erregung zugeordnet werden kann. Der Verlauf über die Erregerfrequenz ist der Amplituden- bzw. Phasengang.

Für den zwei-Massen-Schwinger aus dem #Bild oben mit den Parametern aus der Tabelle sind der Amplituden- und Phasengang im Bild dargestellt.

Größe	F1	F2	m1	m2	k1	k3	k2	α	β
Dimension	MLT−2		M		MT−2			T−1	T
Zahlenwert	0	1	2	1	1	1	1	0	0,01

Amplituden- und Phasengang des zwei-Massen-Schwingers

Analysten erkennen hier:

einen Schwingungsmode ① bei Ω=0,8/s

Die Massen schwingen hier gleichsinnig, zu erkennen an den Phasenwinkeln φ_1,2, die bei Ω=0,8/s gleich sind, und sie schwingen dort mit größerer Amplitude als beim zweiten Mode.

einen zweiten Mode ② bei Ω=1,54/s

Hier schwingen die Massen gegensinnig, denn die Phasenwinkel φ_1,2 weisen eine Differenz von π auf.

eine Antiresonanz ③ bei Ω=1/s

Hier wird die Erregerkraft an der Masse 2 durch die Masse 1 kompensiert, die gegensinnig zur Erregerkraft schwingt (mit Phasenwinkel ≈-π≘-180°). Die Masse 1 wirkt hier als Schwingungstilger.

Schwingungen der Kontinua

Transversalschwingung eines Balkens

Wie im Abschnitt #Einteilung von Schwingungen und Grundbegriffe angedeutet kann ein Balken als ganzes Schwingbewegungen

• in Balkenlängsrichtung als Längs- oder Longitudinalschwingung,
• in Querrichtung als Quer- oder Transversalschwingung in einer bestimmten Schwingungsebene und
• bei Verwindung als Verdreh- oder Torsionsschwingung

ausführen. Flächentragwerke können ebenfalls Schwingungen ausführen.^[6]:B42ff Kontinua besitzen theoretisch unendlich viele Eigenschwingungsformen, die in ihre Grundschwingung mit der niedrigsten Eigenkreisfrequenz und ihre Harmonischen eingeteilt werden. In Resonanzkörpern wird dies ausgenutzt.

Zur Aufstellung der Schwingungsgleichung werden die Verschiebungen infolge einer Streckenlast bzw. Flächenlast berechnet und diese dann als Ursache einer Beschleunigung aufgefasst.^[10]:112 Die Längskoordinate ist x und eine Ableitung nach x wird mit einem Strich wie in u' angezeigt. Bei Tragwerken mit konstanten Eigenschaften über ihre Länge bzw. Fläche ergeben sich die Schwingungsgleichungen aus der Tabelle:

Art	FHG	Schwingungsgleichung
Stabwerke und Seile
Longitudinal	Längung u	${\displaystyle {\ddot {u}}={\frac {E}{\rho }}u''}$
Transversal	Durchbiegung w	${\displaystyle {\ddot {w}}=-{\frac {EI}{\rho A}}w''''}$
Torsion	Torsionswinkel φ	${\displaystyle {\ddot {\varphi }}={\frac {GlI_{t}}{J}}\varphi ''}$
Saitenschwingung	Auslenkung w	${\displaystyle {\ddot {w}}={\frac {S_{1}}{\rho A}}w''}$
Flächentragwerke
Membranen	Durchbiegung w(x,y)	${\displaystyle \mu {\ddot {w}}=S_{2}\Delta w}$
Platten	Durchbiegung w(x,y)	${\displaystyle {\ddot {w}}=-{\frac {N}{\rho h}}\Delta \Delta w}$

Darin is

Zeichen	Bedeutung	Dimension
l,h	Länge, Dicke	L
A	Querschnitt	L2
E	Elastizitätsmodul	ML−1T−2
ρ	Dichte	ML−3
I	Flächenträgheitsmoment	L4
J	Massenträgheitsmoment	ML2
It	Torsionsflächenmoment 2. Grades, das bei kreis- oder kreisringförmigem Querschnitt gleich dem polaren Flächenträgheitsmoment Ip ist.	L4
S1	Spannkraft	MLT−2
μ	Masse je Flächeneinheit	ML−2
S2	Spannkraft pro Längeneinheit	MT−2
𝚫	Laplace-Operator in der Ebene	L−2
N	Plattensteifigkeit	ML2T−2

Die Lösung der Schwingungsgleichung erfolgt mit Trennung der Veränderlichen und dem Produktansatz für den Freiheitsgrad, beispielsweise u(x)=U(x)·T(t) bei der Longitudinalschwingung:

${\displaystyle c^{2}:={\frac {E}{\rho }}\;\rightarrow \;{\ddot {u}}=U{\ddot {T}}=c^{2}u''=c^{2}U''T\quad \rightarrow \quad {\frac {\ddot {T}}{T}}=c^{2}{\frac {U''}{U}}}$

Weil die linke Seite nur von der Zeit t und die rechte nur von der x-Koordinate abhängt, kann die letzte Gleichung auf der ganzen Länge und zu beliebigen Zeitpunkten nur dadurch erfüllt werden, dass die Brüche Konstanten ergeben:

${\displaystyle {\frac {\ddot {T}}{T}}=-\omega ^{2}\;\rightarrow \;{\ddot {T}}+\omega ^{2}T=0,\quad c^{2}{\frac {U''}{U}}=-\omega ^{2}\;\rightarrow \;U''+\lambda ^{2}U=0,\;\lambda ={\frac {\omega }{c}}}$

Diese Differentialgleichungen sind genauso zu lösen wie beim ungedämpften Schwinger und benötigen jeweils zwei Anfangs- und Randbedingungen, siehe Navier-Cauchy-Gleichungen#Beispiel.

Bei der Transversalschwingung des Balkens und der Plattenschwingung treten vierte Ableitungen auf, wodurch die Gleichungen auch von Hyperbelfunktionen erfüllt werden. Hier werden zwei Anfangs- und vier Randbedingungen für die eindeutige Lösung benötigt.^[10]:111f

Bei den Flächentragwerken entsteht mit derselben Methode die Helmholtz-Gleichung, die ihrerseits in vielen orthogonalen Koordinatensystemen durch Trennung der Veränderlichen gelöst werden kann. Das ist hilfreich, wenn die Berandung der Flächenträger in diesen Koordinatensystemen mit Koordinatenlinien übereinstimmen.

Siehe auch

Die folgenden Seiten enthalten Links auf themenrelevante Artikel

• zu Schwingungen:
  • Kategorie:Schwingungen
    • darunter Kategorie:Schwingung: Schwingungsarten
  • Kategorie:Schwingungslehre
  • Kategorie:Schwingungsdynamik: technische Erzeugung und Dämpfung mechanischer Schwingungen
  • Kategorie:Schwingungstechnik-, Feder- oder Dämpfungshersteller
• zu Wellen:
  • Kategorie:Welle: räumlich und zeitlich veränderliche Felder, die Energie, jedoch keine Materie, durch den Raum transportieren.
  • Kategorie:Wellenlehre

Weblinks

Commons: Mechanische Schwingung – Sammlung von Bildern, Videos und Audiodateien

Commons: Harmonische Schwingung – Sammlung von Bildern, Videos und Audiodateien

Literatur

1. D. Gross, W. Hauger, J. Schröder, W. A. Wall: Technische Mechanik 3. Kinetik. 11. Auflage. Springer Vieweg Verlag, Heidelberg 2010, ISBN 978-3-642-11263-8, doi:10.1007/978-3-642-11264-5 (Hierauf beziehen sich die Seitenangaben im Text). Eine neuere Auflage ist: D. Gross, W. Hauger, J. Schröder, W. A. Wall: Technische Mechanik 3. Kinetik. 15. Auflage. Springer Vieweg Verlag, Heidelberg 2021, ISBN 978-3-662-63064-8, S. 61, doi:10.1007/978-3-662-63065-5 (Bewegung eines Massenpunktes).
2. H. Jäger, R. Mastel, M. Knaebel: Technische Schwingungslehre. Grundlagen - Modellbildung - Anwendungen. Springer Vieweg, Wiesbaden 2016, ISBN 978-3-658-13792-2, doi:10.1007/978-3-658-13793-9 (Hierauf beziehen sich die Seitenangaben im Text).
3. P. Hagedorn, S. Otterbein: Technische Schwingungslehre. Lineare Schwingungen diskreter mechanische Systeme. Springer, Berlin, Heidelberg 1987, ISBN 3-540-18096-6, doi:10.1007/978-3-642-83164-5.
4. H. Dresig, F. Holzweißig: Maschinendynamik. 12. Auflage. Springer-Vieweg, 2016, ISBN 978-3-662-52712-2, doi:10.1007/978-3-662-52713-9.
5. M. Jaeger, M. Franck, K. Hameyer: Die Messung und Berechnung modaler Dämpfungen als Näherungsbeschreibung realer Systeme. In: Elektrotechnik und Informationstechnik. Band 139, 2022, S. 195–203, doi:10.1007/s00502-022-01009-0.
6. Karl-Heinrich Grote, Jörg Feldhusen (Hrsg.): Dubbel. Taschenbuch für den Maschinenbau. 25. Auflage. Springer Vieweg Verlag, Berlin, Heidelberg 2019, ISBN 978-3-662-54804-2, S. B36 ff., doi:10.1007/978-3-662-54805-9.

7. 

   Rollschwinger

   Der Rollschwinger ist ein zylindrischer Körper (grau im Bild, Masse m, Drehmasse bezogen auf die Schwerachse J) der auf einer horizontalen Ebene in x-Richtung î hin- und herrollen kann, und dabei von einer im Schwerpunkt angreifenden Feder k gehalten wird. Der Momentanpol liegt im Aufstandspunkt, um den der Zylinder nach dem steinerschen Satz das Massenträgheitsmoment J_M=J+mr² besitzt. Die Rollbedingung x = θ·r und der Drallsatz um den Momentanpol liefern

   ${\displaystyle {\begin{aligned}(J+mr^{2}){\ddot {\theta }}=(J+mr^{2}){\frac {\ddot {x}}{r}}=&-rkx\\\rightarrow \;{\ddot {x}}+{\frac {k}{m+{\frac {J}{r^{2}}}}}x=&0\end{aligned}}}$

   Hieraus identifizieren sich die Ersatzgrößen für den Einfachen Schwinger zu

   ${\displaystyle k_{\text{ers}}=k,\quad m_{\text{ers}}=m+{\frac {J}{r^{2}}}.}$

   siehe H. Jäger, R. Mastel, M. Knaebel (2016), S. 35f.
8. Systeme mit Dämpfungsgrad D>1 werden in der (alten) Norm DIN 1311-2 von 1974 als „stark gedämpft“ bezeichnet. Die neue DIN-Bezeichnung ist „sehr stark gedämpft,“ siehe Jäger, Mastel, Knaebel (2016), S. 96.
9. Im Umkehrpunkt bleibt die Masse stehen und es tritt Haftreibung ein. Der Körper setzt sich nur dann wieder in Bewegung, wenn die Federkraft die Haftreibungskraft überwindet, die oft stärker ist als die Reibkraft bei Gleitreibung, siehe Gross, Hauger, Schröder, Wall (2010), S. 239, und Reibungskoeffizient#Beispiele.
10. H. Balke: Einführung in die Technische Mechanik. Festigkeitslehre. 3. Auflage. Springer-Vieweg, 2014, ISBN 978-3-642-40980-6, doi:10.1007/978-3-642-40981-3.