Gammaverteilung

Die Gammaverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie ist einerseits eine direkte Verallgemeinerung der Exponentialverteilung und andererseits eine Verallgemeinerung der Erlang-Verteilung für nichtganzzahlige Parameter. Wie diese wird sie beispielsweise verwendet

• in der Warteschlangentheorie, um Bedienzeiten oder Reparaturzeiten zu beschreiben;
• in der Versicherungsmathematik, um kleinere bis mittlere Schäden zu modellieren.

Definition

Die Gammaverteilung ${\displaystyle {\mathcal {G}}(p,\,b)}$ ist durch die Wahrscheinlichkeitsdichte ${\displaystyle f(x)={\begin{cases}{\frac {\displaystyle b^{p}}{\displaystyle \Gamma (p)}}x^{p-1}e^{-bx}&x>0\\0&x\leq 0\end{cases}}}$ definiert. Sie besitzt die reellen Parameter ${\displaystyle b}$ und ${\displaystyle p}$. Der Parameter ${\displaystyle b}$ ist ein inverser Skalenparameter und der Parameter ${\displaystyle p}$ ist ein Formparameter. Um ihre Normierbarkeit zu garantieren, wird ${\displaystyle b>0}$ und ${\displaystyle p>0}$ gefordert. Der Vorfaktor ${\displaystyle b^{p}/\Gamma (p)}$ dient der korrekten Normierung; der Ausdruck ${\displaystyle \Gamma (p)}$ steht für den Funktionswert der Gammafunktion, nach der die Verteilung auch benannt ist.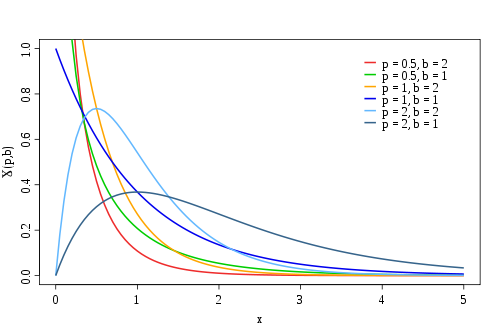

Die Gammaverteilung genügt damit der Verteilungsfunktion ${\displaystyle F(x)={\begin{cases}P(p,bx)&x\geq 0\\0&x<0,\end{cases}}}$ wobei ${\displaystyle P(p,\,bx)}$ die regularisierte Gammafunktion der oberen Grenze ist.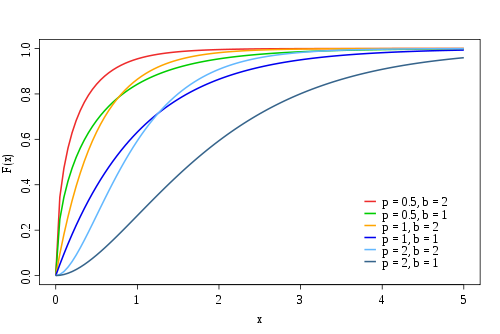

Alternative Parametrisierung

Alternativ zur obigen, im deutschsprachigen Raum üblichen Parametrisierung mit ${\displaystyle p}$ und ${\displaystyle b}$ findet man auch häufig

${\displaystyle (\alpha =p,\beta =b)}$ oder ${\displaystyle \left(k=p,\theta ={\frac {1}{b}}\right).}$

${\displaystyle \beta =b}$ ist die Umkehrung eines Skalenparameters und ${\displaystyle \theta =1/b}$ ist der Skalenparameter selbst. Dichte und Momente ändern sich dementsprechend bei diesen Parametrisierungen (der Erwartungswert wäre hier beispielsweise ${\displaystyle \alpha /\beta }$ beziehungsweise ${\displaystyle k\theta }$). Da diese Parametrisierungen im angelsächsischen Raum vorherrschen, werden sie besonders häufig in der Fachliteratur verwendet. Um Missverständnissen vorzubeugen, wird empfohlen, die Momente explizit anzugeben, also beispielsweise von einer Gammaverteilung mit Erwartungswert ${\displaystyle p/b}$ und Varianz ${\displaystyle p/b^{2}}$ zu sprechen. Hieraus sind dann Parametrisierung und die entsprechenden Parameterwerte eindeutig rekonstruierbar.

Eigenschaften

Die Dichte ${\displaystyle f}$ besitzt für ${\displaystyle p>1}$ an der Stelle ${\displaystyle x_{M}={\tfrac {p-1}{b}}}$ ihr Maximum und für ${\displaystyle p>2}$ an den Stellen

${\displaystyle x_{W}=x_{M}\pm {\frac {(p-1)^{\frac {1}{2}}}{b}}}$

Wendepunkte.

Erwartungswert

Der Erwartungswert der Gammaverteilung ist

${\displaystyle \operatorname {E} (X)={p \over b}.}$

Varianz

Die Varianz der Gammaverteilung ist

${\displaystyle \operatorname {Var} (X)={p \over b^{2}}.}$

Schiefe

Die Schiefe der Verteilung ist gegeben durch

${\displaystyle \operatorname {v} (X)={\frac {2}{\sqrt {p}}}.}$

Reproduktivität

Die Gammaverteilung ist reproduktiv: Die Summe aus den stochastisch unabhängigen gammaverteilten Zufallsvariablen ${\displaystyle X}$ und ${\displaystyle Y}$ mit den Parametern ${\displaystyle b}$ und ${\displaystyle p_{x}}$ bzw. ${\displaystyle p_{y}}$, ist wiederum gammaverteilt mit den Parametern ${\displaystyle b}$ und ${\displaystyle p_{x}+p_{y}}$.

Charakteristische Funktion

Die charakteristische Funktion hat die Form

${\displaystyle \phi _{X}(s)=\left({\frac {b}{b-is}}\right)^{p}.}$

Momenterzeugende Funktion

Die momenterzeugende Funktion der Gammaverteilung ist

${\displaystyle m_{X}(s)=\left({\frac {b}{b-s}}\right)^{p}.}$

Entropie

Die Entropie der Gammaverteilung beträgt

${\displaystyle H(X)=\ln \left(\Gamma (p)\right)-\ln \left(b\right)+(1-p)\psi (p)+p}$

wobei ${\displaystyle \psi (p)}$ die Digamma-Funktion bezeichnet.

Summe gammaverteilter Zufallsgrößen

Sind ${\displaystyle X_{1}\sim {\mathcal {G}}(p_{1},b)}$ und ${\displaystyle X_{2}\sim {\mathcal {G}}(p_{2},b)}$ unabhängige gammaverteilte Zufallsgrößen dann ist auch die Summe ${\displaystyle X_{1}+X_{2}}$ gammaverteilt, und zwar

${\displaystyle X_{1}+X_{2}\sim {\mathcal {G}}(p_{1}+p_{2},b).}$

Allgemein gilt: Sind ${\displaystyle X_{i}\sim {\mathcal {G}}(p_{i},b)\quad i=1,\ldots ,n}$ stochastisch unabhängig dann ist

${\displaystyle X_{1}+\dotsb +X_{n}\sim {\mathcal {G}}(p_{1}+\dotsb +p_{n},b).}$

Somit bildet die Gammaverteilung eine Faltungshalbgruppe in einem ihrer beiden Parameter.

Beziehung zu anderen Verteilungen

Beziehung zur Betaverteilung

Wenn ${\displaystyle X\sim {\mathcal {G}}(p_{1},b)}$ und ${\displaystyle Y\sim {\mathcal {G}}(p_{2},b)}$ unabhängige gammaverteilte Zufallsvariablen sind mit den Parametern ${\displaystyle p_{1},b}$ bzw. ${\displaystyle p_{2},b}$, dann ist die Größe ${\displaystyle {\tfrac {X}{X+Y}}}$ betaverteilt mit Parametern ${\displaystyle p_{1}}$ und ${\displaystyle p_{2}}$, kurz

${\displaystyle \operatorname {Beta} (p_{1},p_{2})\sim {\frac {{\mathcal {G}}(p_{1},b)}{{\mathcal {G}}(p_{1},b)+{\mathcal {G}}(p_{2},b)}}.}$

Beziehung zur Chi-Quadrat-Verteilung

• Die Chi-Quadrat-Verteilung mit ${\displaystyle k}$ Freiheitsgraden ist eine Gammaverteilung mit den Parametern ${\displaystyle p=k/2}$ und ${\displaystyle b=1/2}$.

Beziehung zur Erlang-Verteilung

Die Erlang-Verteilung mit dem Parameter ${\displaystyle \lambda }$ und ${\displaystyle n}$ Freiheitsgraden entspricht einer Gammaverteilung mit den Parametern ${\displaystyle p=n}$ und ${\displaystyle b=\lambda }$ und liefert die Wahrscheinlichkeit der Zeit bis zum Eintreffen des ${\displaystyle p}$-ten seltenen, Poisson-verteilten Ereignisses.

Beziehung zur Exponentialverteilung

• Wählt man in der Gammaverteilung den Parameter ${\displaystyle p=1}$, so erhält man die Exponentialverteilung mit Parameter ${\displaystyle \lambda =b}$.
• Die Faltung von ${\displaystyle n}$ Exponentialverteilungen mit demselben ${\displaystyle \lambda }$ ergibt eine Gamma-Verteilung mit ${\displaystyle p=n,b=\lambda }$.

Beziehung zur logarithmischen Gammaverteilung

Ist ${\displaystyle X}$ Gamma-verteilt, dann ist ${\displaystyle Y=e^{X}}$ Log-Gamma-verteilt.

Literatur

• Bernard W. Lindgren: Statistical Theory. Chapman & Hall, New York u. a. 1993, ISBN 0-412-04181-2.
• Marek Fisz: Wahrscheinlichkeitsrechnung und mathematische Statistik. 11. Auflage. Deutscher Verlag der Wissenschaften, Berlin 1989, ISBN 3-326-00079-0.
• P. Heinz Müller (Hrsg.): Wahrscheinlichkeitsrechnung und Mathematische Statistik. 5., bearb. und wesentlich erw. Auflage. Akad.-Verlag, Leipzig 1991, ISBN 3-05-500608-9

Weblinks

• siehe auch Lévy-Prozess, mit Bild von einem Gamma-Prozess
• Interaktives Applet der Universität Konstanz zum Darstellen der Gammaverteilung: http://www.uni-konstanz.de/FuF/wiwi/heiler/os/vt-gamma.html
• Gerechnete Beweise: http://www.eisber.net/StatWiki/index.php/WS2_Zettel1#Gamma-Verteilung

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | Dirac | diskret uniform | empirisch | hypergeometrisch | kategorial | negativ hypergeometrisch | Rademacher | verallgemeinert binomial | Zipf | Zipf-Mandelbrot | Zweipunkt

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | discrete-Phase-Type | erweitert negativ binomial | Gauss-Kuzmin | gemischt Poisson | geometrisch | logarithmisch | negativ binomial | parabolisch-fraktal | Poisson | Skellam | verallgemeinert Poisson | Yule-Simon | Zeta

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Cantor | Kumaraswamy | raised Cosine | Dreieck | Trapez | U-quadratisch | stetig uniform | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi | Chi-Quadrat | Coxian | Erlang | Exponential | Extremwert | F | Fermi-Dirac | Folded normal | Fréchet | Gamma | Gamma-Gamma | verallgemeinert invers Gauß | halblogistisch | halbnormal | Hartman-Watson | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | invers Chi-Quadrat | scale-invers Chi-Quadrat | Invers Normal | Invers Gamma | Kolmogorow-Verteilung | Lévy | log-normal | log-logistisch | Maxwell-Boltzmann | Maxwell-Speed | Nakagami | nichtzentriert Chi-Quadrat | Pareto | Phase-Type | Rayleigh | relativistisch Breit-Wigner | Rice | Rosin-Rammler | shifted Gompertz | truncated normal | Type-2-Gumbel | Weibull | Wilks’ Lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | exponential Power | Fishers z | Fisher-Tippett (Gumbel) | generalized hyperbolic | Hyperbolic-secant | Landau | Laplace | alpha-stabil | logistisch | normal (Gauß) | normal-invers Gauß’sch | Skew-normal | Studentsche t | Type-1-Gumbel | Variance-Gamma | Voigt

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Dirichlet compound multinomial | Ewens | gemischt Multinomial | multinomial | multivariat hypergeometrisch | multivariat Poisson | negativmultinomial | Pólya/Eggenberger | polyhypergeometrisch

Kontinuierliche multivariate Verteilungen:
Dirichlet | GEM | generalized Dirichlet | multivariat normal | multivariat Student | normalskaliert invers Gamma | Normal-Gamma | Poisson-Dirichlet

Multivariate Matrixverteilungen:
Gleichverteilung auf der Stiefel-Mannigfaltigkeit | Invers Wishart | Matrix Beta | Matrix Gamma | Matrix invers Beta | Matrix invers Gamma | Matrix Normal | Matrix Student-t | Matrix-Von-Mises-Fisher-Verteilung | Normal-invers-Wishart | Normal-Wishart | Wishart