在幾何學中,七角柱是一種多面體,是柱體的一種,是指底面是七邊形的柱體。所有七角柱都有9個面,21個邊和14個頂點[1]。所有七角柱都是九面體。
事实速览 類別, 對偶多面體 ...
正七角柱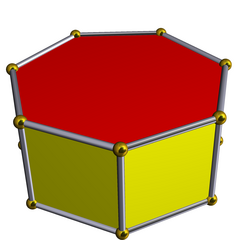 |
| 類別 | 柱體
柱狀均勻多面體 |
|---|
| 對偶多面體 | 雙七角錐 |
|---|
|
考克斯特符號
|     
    
     |
|---|
| 施萊夫利符號 | t{2,7}
{7}×{} |
|---|
威佐夫符號
| 2 7 | 2 |
|---|
| 康威表示法 | P7 |
|---|
|
| 面 | 9 |
|---|
| 邊 | 21 |
|---|
| 頂點 | 14 |
|---|
| 歐拉特徵數 | F=9, E=21, V=14 (χ=2) |
|---|
|
| 面的種類 | 2個七邊形
7個正方形 |
|---|
面的佈局
| 7{4}+2{7} |
|---|
| 頂點圖 | 4.4.7 |
|---|
|
| 對稱群 | D7h, [7,2], (*722), order 28 |
|---|
旋轉對稱群
| D7, [7,2]+, (722), order 14 |
|---|
|
| 凸、 zonohedron、 半正 |
|
|
|
|
关闭
如果七角柱每個面都是正多邊形,則它是半正多面體。
正七角柱可以視為一種半正多面體,底面為正七邊形,其施萊夫利符號可以用t{2,7}或{7}x{}表示,t{2,7}是指正七角柱可以藉由七面形透過截角變換構造而來,其在威佐夫符號中用2 7 | 2表示[2]。
正七角柱有二種兩面角,其中一個為90度,即頂面(或底面)與側面的夾角,另一個是 度[3],即兩側面的夾角。
度[3],即兩側面的夾角。
正七角柱是一種比較特殊的多面體,由於他具有一個非整數的有理數角度,且與正六角柱接近[4],因此在工程學上有些應用,例如正七角柱可以用在特殊汽缸的設計[5]、正七角柱的稜鏡可以用在干涉濾光器的光信號多路復用器中[6]。除此之外,正七角柱也出現在自然界中,例如碘合氮化硼化鎂(Mg8[BN2]5I)的碘離子為正七角柱的晶體結構[7],例如伊樂藻,有91%的親本細胞為正七角柱[8]。
此外,也有人設計七角柱形的魔術方塊[9],或是經過截角變換的七角柱[10][11]。
更多信息 [7,2]+, (722), 半正對偶 ...
半正七邊形二面體球面多面體
| 對稱群:[7,2], (*722)
|
[7,2]+, (722)
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|

|

|

|

|

|
|

|

|
| {7,2}
|
t{7,2}
|
r{7,2}
|
2t{7,2}=t{2,7}
|
2r{7,2}={2,7}
|
rr{7,2}
|
tr{7,2}
|
sr{7,2}
|
| 半正對偶
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|

|

|

|

|

|

|

|

|
| V72
|
V142
|
V72
|
V4.4.7
|
V27
|
V4.4.7
|
V4.4.14
|
V3.3.3.7
|
关闭
更多信息 球面鑲嵌, 柱體 ...
柱體形式半正鑲嵌系列:
| 球面鑲嵌
|
柱體
|
歐式鑲嵌
仿緊空間
|
雙曲鑲嵌
非緊空間
|

t{2,1}
  
|

t{2,2}
    
|

t{3,2}
    
|

{4,2}
    
|

t{5,2}
    
|

t{6,2}
    
|

t{7,2}
    
|

t{8,2}
    
|
...
|

t{2,∞}
    
|

t{2,iπ/λ}
    
|
关闭
Guest, Simon D., and Sergo Pellegrino. "The folding of triangulated cylinders, Part I: Geometric considerations." Journal of applied mechanics 61.4 (1994): 773-777.
Ishikawa, Shigeta. "Optical multiplexer/demultiplexer using interference filters." U.S. Patent No. 4,482,994. 13 Nov. 1984.
Somer, Mehmet, et al. "Mg2[BN2]Cl and Mg8[BN2]5I: Novel Magnesium Nitridoborate Halides—Syntheses, Crystal Structures, and Vibrational Spectra." Zeitschrift für anorganische und allgemeine Chemie 630.7 (2004): 1015-1021.
Van Fleet, D. S. "A comparison of histochemical and anatomical characteristics of the hypodermis with the endodermis in vascular plants." American Journal of Botany (1950): 721-725.