三尖瓣线

三尖瓣线（tricuspoid）也稱為施泰纳曲線（Steiner curve），是有三個尖點的圆内螺线，是一個圓繞著直徑為其三倍的圓內側無滑動滾動時，圓上一點產生的一般旋轮线

紅色的即為三尖瓣线

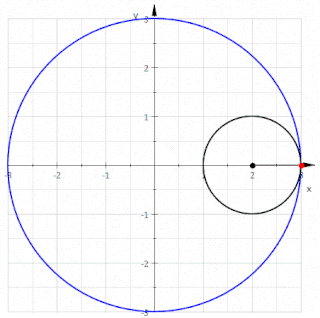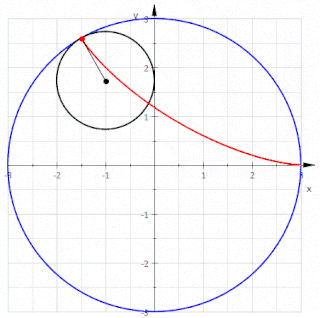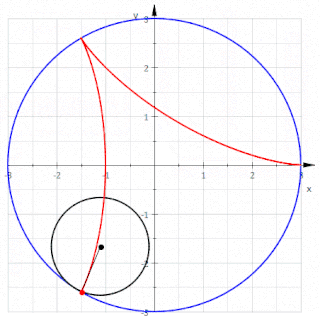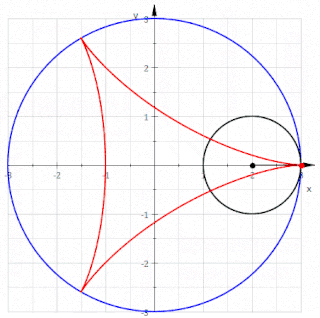
三尖瓣线也可以指有三個頂點，之間用向內彎曲的曲線相連的封閉空間，因此三尖瓣线內的空間是非凸集合^[1]。

方程式

三尖瓣线可以用以下的參數方程表示：

${\displaystyle x=(b-a)\cos(t)+a\cos \left({\frac {b-a}{a}}t\right)\,}$

${\displaystyle y=(b-a)\sin(t)-a\sin \left({\frac {b-a}{a}}t\right)\,,}$

其中a是小圓的半徑，b是大圓（也就是小圓在其內側無滑動滾動）的半徑（此處b = 3a）。

在複變座標下可得

${\displaystyle z=2ae^{it}+ae^{-2it}}$.

上述的t可以消去，得到以下的笛卡爾座標下的方程

${\displaystyle (x^{2}+y^{2})^{2}+18a^{2}(x^{2}+y^{2})-27a^{4}=8a(x^{3}-3xy^{2}),\,}$

因此三尖瓣线是四階的代數曲線，在極坐標下為

${\displaystyle r^{4}+18a^{2}r^{2}-27a^{4}=8ar^{3}\cos 3\theta \,.}$

曲線有三個奇點，是對應${\displaystyle t=0,\,\pm {\tfrac {2\pi }{3}}}$的尖點。上述的參數式意味者曲線為有理曲線，也就表示其幾何虧格（英语：geometric genus）為零。

三尖瓣线的對偶曲線（英语：dual curve）為

${\displaystyle x^{3}-x^{2}-(3x+1)y^{2}=0,\,}$

在原點有一個二重點，若進行一個虛軸上的旋轉y ↦ iy，曲線會變為下式，就可以看到其二重點

${\displaystyle x^{3}-x^{2}+(3x+1)y^{2}=0\,}$

在實平面的原點上有二重點。

面積及周長

三尖瓣线的面積為${\displaystyle 2\pi a^{2}}$，其中a為小圓的半徑，其面積是小圓面積的兩倍^[2]。

其周長為16a^[2]。

歷史

早在1599年時，伽利略·伽利莱及马兰·梅森就已開始研究常見的摆线，而奧勒·羅默在1674年研究齒輪的最佳外形時，也有用到摆线。李昂哈德·歐拉認為他是最早（1745年）將三尖瓣线應用在實際光學問題的人。

應用

三尖瓣线有應用在許多的數學領域中，舉例如下：

• 三維unistochastic（英语：unistochastic）矩陣複數特徵值的集合即為三尖瓣线。
• SU(3)群裡所有酉矩阵的可能跡的集合會組成三尖瓣线。
• 二個三尖瓣线的交集會形成一群6階的複數Hadamard矩陣（英语：Complex Hadamard matrix）。
• 三角形的所有西姆松線的集合，其包絡線會是三尖瓣线。因為雅各布·施泰纳在1856年描述過此曲線的形狀及對稱性，因此此曲線稱為這稱為施泰纳三尖瓣线，^[3]。
• 三角形面積平分線的包絡線會是三尖瓣线，三個頂點是中線的中點。三尖瓣线的三邊是双曲线的弧^[4][1]。
• 三尖瓣线屬於掛谷集（英语：Kakeya set）中的掛谷針集合（Kakeya needle set，長度為1的針可以在其中旋轉360度），有科學家認為三尖瓣线是掛谷針問題（Kakeya needle problem，面積最小小的掛谷針集合）的解，後來發現不是。

相關條目

• 星形线：有三個尖點的圆内螺线
• 伪三角形（英语：Pseudotriangle）
• 勒洛三角形
• 超橢圓

参考资料

1. 存档副本. [2017-10-24]. （原始内容存档于2017-11-21）.
2. Weisstein, Eric W. "Deltoid." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Deltoid.html （页面存档备份，存于互联网档案馆）
3. Lockwood
4. Dunn, J. A., and Pretty, J. A., "Halving a triangle," Mathematical Gazette 56, May 1972, 105-108.

• E. H. Lockwood. Chapter 8: The Deltoid. A Book of Curves. Cambridge University Press. 1961.
• J. Dennis Lawrence. A catalog of special plane curves. Dover Publications. 1972: 131–134. ISBN 0-486-60288-5.
• Wells D. The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. 1991: 52. ISBN 0-14-011813-6.
• "Tricuspoid" at MacTutor's Famous Curves Index（页面存档备份，存于互联网档案馆）
• "Deltoid" at MathCurve（页面存档备份，存于互联网档案馆）
• Sokolov, D.D., Steiner curve, Hazewinkel, Michiel (编), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4