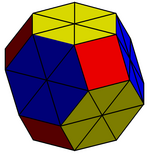
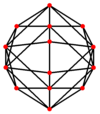
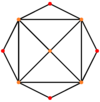
在幾何學 中,截角八面體 [ 1] 半正多面體 ,屬於阿基米德立體 也是個平行多面體 。由6個正方形 和8個正六邊形 組成,共有14 個面 、36 個邊 以及24 個頂點 [ 2] 環帶多面體 。同時,因為它具有正方形和六邊形面,因此也是一種戈德堡多面體 ,其戈德堡符號 為GIV (1,1)。另外,由於截角八面體也是一種排列多面體 [ 3] [ 4] [ 5] 截角八面體堆砌 [ 6]
Quick Facts 類別, 對偶多面體 ...
截角八面體 (按這裡觀看旋轉模型) 類別 半正多面體 對偶多面體 四角化立方體 名稱 截角八面體 參考索引 U 08 , C 20 , W 7 鮑爾斯縮寫 toe 考克斯特符號 施萊夫利符號 t0,1 {3,4}0,1,2 {3,3} 威佐夫符號 2 4 | 3 康威表示法 tO bT 面 14 邊 36 頂點 24 歐拉特徵數 F=14, E=36, V=24 (χ=2) 面的種類 正方形 正六邊形 面的佈局 6個{4} 頂點圖 4.6.6 對稱群 Oh 群 Th 環帶多面體
Close
截角八面體的對偶多面體為四角化六面體 。若截角八面體的邊長 為單位長,則其對偶多面體四角化六面體 的邊長會變成
9
8
2
{\displaystyle {\tfrac {9}{8}}\scriptstyle {\sqrt {2}}}
3
2
2
{\displaystyle {\tfrac {3}{2}}\scriptstyle {\sqrt {2}}}
截角八面體僅具有點可遞性質,也就是截角八面體每一個頂點相鄰面的組成都是一樣的,都是一個四邊形和兩個六邊形的公共頂點。但截角八面體不具面可遞和邊可遞性質,因為截角八面體有兩種面,四邊形和六邊形,邊也不可遞,因為截角八面體並不是所有組成邊的相鄰面都只有一種,截角八面體共有兩種稜,一種為六邊形與六邊形的公共稜、另一種為六邊形與四邊形的公共稜。
由於截角八面體僅具有點可遞性質,因此只能算是均勻多面體 [ 7] 半正多面體 ,不具擬正多面體 性質。但這個多面體是阿幾米德研究的13種半正多面體之一,因此截角八面體也是一種阿基米德立體 [ 8]
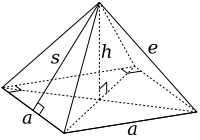
截角八面體可以從邊長3a的正八面體 切去六個底邊長為a的四角錐 構成。這些被切下來的棱錐體的底與側面邊長皆等長,因此其側面皆為正三角形,底邊長為a、底面積為a2 ,這些四角錐是正四角錐 ,是第一種詹森多面體 ,J1 。
這些被截下來的正四角錐 其高h與斜高s為:
h
=
e
2
−
1
2
a
2
=
2
2
a
{\displaystyle h={\sqrt {e^{2}-{\frac {1}{2}}a^{2}}}={\frac {\sqrt {2}}{2}}a}
s
=
h
2
+
1
4
a
2
=
1
2
a
2
+
1
4
a
2
=
3
2
a
{\displaystyle s={\sqrt {h^{2}+{\frac {1}{4}}a^{2}}}={\sqrt {{\frac {1}{2}}a^{2}+{\frac {1}{4}}a^{2}}}={\frac {\sqrt {3}}{2}}a}
這些數據則確定能從正八面體構成截角八面體的截角 切割深度。若太深則會變成截半八面體 。
[ 9]
在(±2,±2,±2)範圍內的平行投影
每個六邊形面切割成六個正三角形產生了八個新的頂點,他們分別為(±1,±1,±1)的所有組合。
邊長為2的平方根 且幾何中心 位於原點 的截角八面體其頂點座標為(0, ±1, ±2)的所有排列。
將正八面體 進行截角操作 ,也就是將正八面體的六個頂點 切去並在被切掉的地方建立六個正方形 面即可得到一個截角八面體 。
More information 平行投影, 施萊格爾投影(英語:Schlegel diagram) ...
Close
截角八面體可分割成正中央一個正八面體、其餘每個面切成8三角帳塔,剩餘的部分在分割成6個正四角錐 。[ 10]
More information 虧格 2, 虧格 3 ...
虧格 2
虧格 3
D3d , [2+ ,6], (2*3), order 12
Td , [3,3], (*332), order 24
Close
截角八面體是一種排列多面體 [ 3] [ 4]
x
+
y
+
z
+
w
=
10
{\displaystyle x+y+z+w=10}
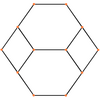
二維 形狀是正六邊形 :三維空間中,(1,2,3)所有排列的坐標在二維子空間
x
+
y
+
z
=
6
{\displaystyle x+y+z=6}
More information 對稱性: [3,3], (*332), [3,3]+, (332) ...
正四面體家族半正多面體
對稱性 : [3,3] , (*332)
[3,3]+ , (332)
{3,3}
t0,1 {3,3}
t1 {3,3}
t1,2 {3,3}
t2 {3,3}
t0,2 {3,3}
t0,1,2 {3,3}
s{3,3}
半正多面體對偶
V3.3.3
V3.6.6
V3.3.3.3
V3.6.6
V3.3.3
V3.4.3.4
V4.6.6
V3.3.3.3.3
Close
More information 對稱性: [4,3], (*432), [4,3]+, (432) ...
半正正八面體家族多面體
對稱性 : [4,3] , (*432)
[4,3]+ , (432)
[1+ ,4,3], (*332)
[4,3+ ], (3*2)
{4,3}
t0,1 {4,3}
t1 {4,3}
t1,2 {4,3}
{3,4}
t0,2 {4,3}
t0,1,2 {4,3}
s{4,3}
h{4,3}
h1,2 {4,3}
半正多面體的對偶
V4.4.4
V3.8.8
V3.4.3.4
V4.6.6
V3.3.3.3
V3.4.4.4
V4.6.8
V3.3.3.3.4
V3.3.3
V3.3.3.3.3
Close
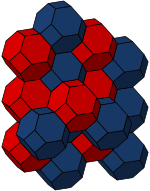
截角八面體可獨立密鋪 三維空間。 截角八面體堆砌 截角八面體可以獨立填滿整個三維空間,而這種由截角八面體堆砌 出來的幾何圖形稱為截角八面體堆砌 。
截角八面體堆砌 是三維空間 內28個半正密鋪之一,由截角八面體獨立堆積而成,雖然他每個胞 都全等、每邊 皆等長,但其不能稱為正密鋪,因為雖然她只由一種胞,截角八面體組成,但是該胞不是正多面體 ,因此並非所有「面」皆全等,因此截角八面體堆砌只能稱為半正堆砌。
其他堆砌 More information 截角八面體堆砌, 小斜方截半正方體堆砌 ...
Close
Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X (Section 3-9)Cayley graph of S4 . This Cayley graph labeling is shown, e.g., by Ziegler (1995) harvtxt error: no target: CITEREFZiegler1995 (help ) . John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things , ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)Cromwell, P. Polyhedra , CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids
Gaiha, P., and Guha, S.K. Adjacent vertices on a permutohedron. SIAM Journal on Applied Mathematics. 1977, 32 (2): 323–327. doi:10.1137/0132025 Alexandrov, A.D. Convex polyhedra. Berlin: Springer. 1958: 539. ISBN 3-540-23158-7 Cromwell, P. Polyhedra . United Kingdom: Cambridge. 1997: 79 –86 Archimedean solids . ISBN 0-521-55432-2