取樣定理

取樣定理是數位訊號處理領域的重要定理。定理內容是連續訊號（通常稱作「類比訊號」）與離散訊號（通常稱作「數位訊號」）之間的一個基本橋梁。它確定了訊號頻寬的上限，或能擷取連續訊號的所有資訊的離散取樣訊號所允許的取樣頻率的下限。

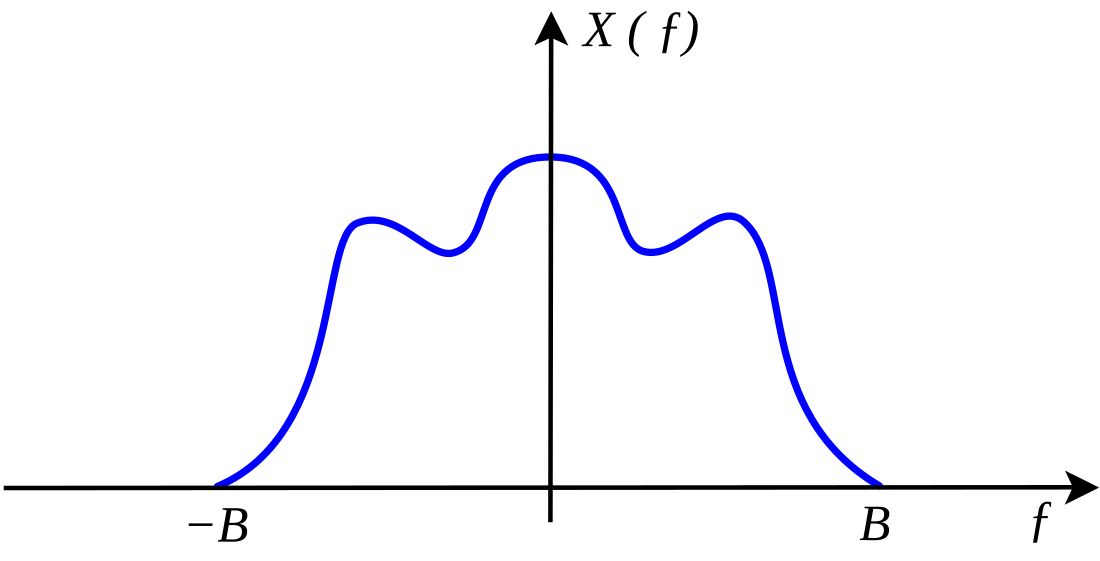
圖1：頻寬限制的函式的傅立葉轉換的模

嚴格地說，定理僅適用於具有傅立葉轉換的一類數學函式，即頻率在有限區域以外為零（參照圖1）。離散時間傅立葉轉換（泊松求和公式的一種形式）提供了實際訊號的解析延拓，但只能近似該條件。直觀上我們希望，當把連續函式化為取樣值（叫做「樣本」）的離散序列並插值到連續函式中，結果的保真度取決於原始取樣的密度（或取樣率）。取樣定理介紹了對頻寬限制的函式類型來說保真度足夠完整的取樣率的概念；在取樣過程中"資訊"實際沒有損失。定理用函式的頻寬來表示取樣率。定理也匯出了一個數學上理想的原連續訊號的重構公式。

該定理沒有排除一些並不滿足取樣率準則的特殊情況下完整重構的可能性。（參見下文非基頻訊號取樣，以及壓縮感知。）

奈奎斯特–夏農取樣定理的名字是為了紀念哈里·奈奎斯特和克勞德·夏農。該定理及其在插值理論中的原型曾被奧古斯丁-路易·柯西、埃米爾·博雷爾、雅克·阿達馬、夏爾-讓·德拉瓦萊·普桑、埃德蒙·泰勒·惠特克、弗拉基米爾·亞歷山德羅維奇·科捷利尼科夫等人發現或研究^[1]:1-4。所以它還叫做奈奎斯特–夏農–科捷利尼科夫定理、惠特克–夏農–科捷利尼科夫定理、惠特克–奈奎斯特–科捷利尼科夫–夏農定理及插值基本定理。

簡介

取樣是將一個訊號（例如時間或空間上連續的函式）轉換為數位序列（時間或空間上離散的函式）的過程。這個定理的夏農版本陳述為：^[2]

如果週期函式 x(t) 不包含高於 B cps（次/秒）的頻率，那麼，一系列小於 1/(2B) 秒的x(t)函式值將會受到前一個週期的x(t)函式值影響。

因此 2B 樣本/秒或更高的取樣頻率將能使函式不受干擾。相對的，對於一個給定的取樣頻率 f_s，完全重構的頻帶限制為 B ＜ f_s/2。

在頻帶限制過高（或根本沒有頻帶限制）的情形下，重構表現出的缺陷稱為混疊。現在對於此定義的陳述有時會很小心的指出x(t)必須不包括頻率恰好為B的正弦曲線，或是B必須小於½的取樣頻率。這二個門檻，2B及f_s/2會稱為奈奎斯特速率（英語：Nyquist rate）及奈奎斯特頻率。這些是x(t)及取樣裝置的屬性。上述的不等式會稱為奈奎斯特準則，有時會稱為拉貝準則（Raabe condition）。此定理也可以用在其他定義域（例如離散系統）的函式下，唯一的不同是量測t, f_s和B的單位。

正規化的Sinc函式：sin(πx) / (πx) ...其中央峰值在x= 0，其他整數值的x時為零交越點

符號 T = 1/f_s 常用來表示二次取樣之間的時間間隔，稱為取樣周期或是取樣區間。函式x(t)的取樣常用x[n] = x(nT)表示（較早期的文獻會用x_n），其中n為正整數。在數學上理想的取樣還原（插值）和Sinc函式有關，每次的取樣都用中心點在取樣時間nT，振幅是取樣值x[n]的Sinc函式代替。最後將Sinc函式加總，得到連續的函式。數學上等效的方式是將Sinc函式和一連串的狄拉克δ函式卷積，再依取樣到的值來加權。不過這些方式在數學上都是不實際的。不過有些有限長度的函式可以近似Sinc函式，這種因為近似的不完美造成的誤差稱為插值誤差（interpolation error）。

實際的數位類比轉換器既不會產生加權而有延遲的Sinc函式，也不會產生理想的狄拉克δ函式，若是其類比重建是用零階保持，其輸出的是由不同振幅及有延遲的矩形函式組成的階躍函式，一般後面會有抗鏡像濾波器（anti-imaging filter）來清除假的高頻成份。

混疊

主條目：混疊

二個正弦波的頻率不同，但其取樣值相關，其中至少有一個的頻率超過取樣頻率的一半

如果不能滿足上述取樣條件，取樣後訊號的頻率就會重疊，即高於取樣頻率一半的頻率成分將被重建成低於取樣頻率一半的訊號。這種頻譜的重疊導致的失真稱為混疊，而重建出來的訊號稱為原訊號的混疊替身，因為這兩個訊號有同樣的樣本值。

若x(t)為一函式，其傅立葉轉換X(f)為:

${\displaystyle X(f)\ {\stackrel {\mathrm {def} }{=}}\ \int _{-\infty }^{\infty }x(t)\ e^{-i2\pi ft}\ {\rm {d}}t,}$

泊松求和公式指出x(t)的取樣x(nT)足以產生X(f)的週期和（英語：periodic summation），結果為：

${\displaystyle X_{s}(f)\ {\stackrel {\mathrm {def} }{=}}\sum _{k=-\infty }^{\infty }X\left(f-kf_{s}\right)=\sum _{n=-\infty }^{\infty }T\cdot x(nT)\ e^{-i2\pi nTf},}$

Eq.1

圖4：X(f)（上圖藍色部份）及X_A(f)（下圖藍色部份）是二個不同函式x(t)及x_A(t)（原函式省略不列出）的連續傅立葉轉換。當二個函式以f_s的速率取樣時，且確認訊號的離散傅立葉轉換（DTFT）時，其鏡相（image，綠色部份）會和轉換後訊號（藍色部份）疊加。在這個假設的例子中，二函式的離散傅立葉轉換相同，表示取樣到的訊號也相同，可是在取樣前的原函式是不同的。若這是聲音訊號，x(t)和x_A(t)聽起來是不一樣的，可是其以f_s速率的取樣是一樣的，因此最後重製的聲音是相同的，x_A(t)是x(t)在此取樣頻率下的混疊（alias）

是一個週期函式，等效為傅立葉級數，係數為T•x(nT)。此函式也稱為數列T•x(nT)的離散時間傅立葉轉換 (DTFT)，n為整數。

如圖4所示，X(f) 的拷貝被平移了 f_s 的倍數，並相加合併。對於一個帶限函式（對所有 |f| ≥ B，X(f) = 0），在 f_s 足夠大的時候，這些拷貝之間仍然分得清楚。但如果奈奎斯特準則並不滿足，相鄰部分就會重疊，一般就不能明確辨別出 X(f)。任何超過 f_s/2 的頻率分量都會與較低的頻率分量難以區分，稱作與其中一個拷貝發生「混疊」。在這種情況下，通常的插值法就會產生混疊，而不是原始的分量了。

以下兩種措施可避免混疊的發生：

1. 提高取樣頻率，使之達到最高訊號頻率的兩倍以上；
2. 引入低通濾波器或提高低通濾波器的參數；該低通濾波器通常稱為抗混疊濾波器

當取樣率預先由其他因素（如行業標準）確定的時候，x(t) 通常要先濾波以將高分頻量減少到可以接受的水平，再進行取樣。所需的濾波器的種類為低通濾波器，而在這種應用中叫做抗混疊濾波器。抗混疊濾波器可限制訊號的頻寬，使之滿足取樣定理的條件。這在理論上是可行的，但是在實際情況中不可能做到。因為濾波器不可能完全濾除奈奎斯特頻率之上的訊號，所以，取樣定理要求的頻寬之外總有一些「小的」能量。不過抗混疊濾波器可使這些能量足夠小，以至可忽略不計。

圖5：X_s(f)是由適當頻寬濾波器濾波後的訊號，其頻譜（藍色）和其相鄰的DTFT鏡像（綠色）不會重疊。brick-wall低通濾波器H(f)可以移除鏡像，留下原始的頻譜X(f)，由取樣後的訊號還原為（濾波後）的原始訊號

由泊松求和的特例來推導

從圖5中可以看到，若X(f)的複本（也稱為鏡像）之間沒有和k = 0的項重疊，可以由X_s(f)用以下的乘積來還原：

${\displaystyle X(f)=H(f)\cdot X_{s}(f),\,}$      where:

${\displaystyle H(f)\ {\stackrel {\mathrm {def} }{=}}\ {\begin{cases}1&|f|<B\\0&|f|>f_{s}-B.\end{cases}}}$

此時證明了取樣定理，因此X(f)可以確定x(t)，而且只有唯一解。

剩下的就只有推導重構的公式。H(f)不需在[B, f_s − B]的區域有準確的定義，因為X_s(f)在此區域為零。不過最壞的情形是B = f_s/2，奈奎斯特頻率。一個在此情形及其他較輕微的條件下都適用的函式為：

${\displaystyle H(f)=\mathrm {rect} \left({\frac {f}{f_{s}}}\right)={\begin{cases}1&|f|<{\frac {f_{s}}{2}}\\0&|f|>{\frac {f_{s}}{2}},\end{cases}}}$

其中rect(•)為矩形函式，因此：

${\displaystyle X(f)=\mathrm {rect} \left({\frac {f}{f_{s}}}\right)\cdot X_{s}(f)\ }$

${\displaystyle =\mathrm {rect} (Tf)\cdot \sum _{n=-\infty }^{\infty }T\cdot x(nT)\ e^{-i2\pi nTf}}$      （根據上面的 Eq.1）

${\displaystyle =\sum _{n=-\infty }^{\infty }x(nT)\cdot \underbrace {T\cdot \mathrm {rect} (Tf)\cdot e^{-i2\pi nTf}} _{{\mathcal {F}}\left\{\mathrm {sinc} \left({\frac {t-nT}{T}}\right)\right\}}.}$     ^[3]

等式二側反轉換，可以得到惠特克-香農插值公式（英語：Whittaker–Shannon interpolation formula）

${\displaystyle x(t)=\sum _{n=-\infty }^{\infty }x(nT)\cdot \mathrm {sinc} \left({\frac {t-nT}{T}}\right),}$

上式就是用取樣值x(nT)來重構x(t)的方式。

• 若f_s大於所需值，也就是T較小，稱為過取樣（oversampling），由圖5可以看出過取樣對重構訊號沒有任何效果，但可以提供一塊「轉態區」，此區域內的H(f)可以是一些非零的值。相反的，欠取樣（英語：Undersampling）會造成混疊，一般而言無法重構原始訊號。
• 理論上，插值公式可以用低通濾波器來實現，其脈衝響應為sinc(t/T)，輸入為${\displaystyle \textstyle \sum _{n=-\infty }^{\infty }x(nT)\cdot \delta (t-nT),}$，即為一個被取樣訊號調變過的脈波序列（英語：Dirac comb）函式。實際的數位類比轉換器（DAC）會用零階保持器（英語：zero-order hold）來近似，此時過取樣可以減少近似的誤差。

夏農的原始證明

泊松證明了Eq.1中的傅立葉級數會產生 X(f) 的周期求和，不管 f_s 和 B 是什麼值。然而夏農只推導了 f_s = 2B 情形下級數的係數。 幾乎參照了夏農原始的論文：

令 ${\displaystyle \scriptstyle X(\omega )}$ 為 ${\displaystyle \scriptstyle x(t)}$ 的頻譜。則

${\displaystyle x(t)\,}$	${\displaystyle ={1 \over 2\pi }\int _{-\infty }^{\infty }X(\omega )e^{i\omega t}\;{\rm {d}}\omega \ }$
	${\displaystyle ={1 \over 2\pi }\int _{-2\pi B}^{2\pi B}X(\omega )e^{i\omega t}\;{\rm {d}}\omega \ }$

因為假設在頻帶 ${\displaystyle \scriptstyle |{\frac {\omega }{2\pi }}|<B}$ 以外 ${\displaystyle \scriptstyle X(\omega )}$ 為零。若我們令

${\displaystyle t={n \over {2B}}\,}$

其中 n 為任意正整數或負整數，我們得到

${\displaystyle x\left({\tfrac {n}{2B}}\right)={1 \over 2\pi }\int _{-2\pi B}^{2\pi B}X(\omega )e^{i\omega {n \over {2B}}}\;{\rm {d}}\omega .}$

在等式左邊的是${\displaystyle \scriptstyle x(t)}$在取樣點的數值，右邊的積分在本質上可以視為是${\displaystyle \scriptstyle X(\omega )}$的n次係數，以–B至B為其基礎週期^{[note 1]}。這表示${\displaystyle \scriptstyle x(n/2B)}$的取樣值也決定了${\displaystyle \scriptstyle X(\omega )}$傅立葉展開的第n次係數。對於比B低的頻率，若其傅立葉係數確定了，${\displaystyle \scriptstyle X(\omega )}$也就確定了，而在高於B的頻率，其數值為零，因此整個${\displaystyle \scriptstyle X(\omega )}$都可以確定。因為一函式的頻譜若確定了，其函式也就確定了，因此${\displaystyle \scriptstyle X(\omega )}$可以完全的決定原始函式，也就表示原始的取樣可以完整的決定函式${\displaystyle \scriptstyle x(t)}$。

夏農對於此定理的證明已經完成了，不過夏農進一步探討用Sinc函式重構原函式，也就是今日的惠特克–夏農內插公式（英語：Whittaker–Shannon interpolation formula），他沒有推導或是證明sinc函式的性質，但這些對於當時閱讀其作品的工程師不會覺得陌生，因為當時已經知道矩形函式和Sinc函式的傅立葉對關係。

令${\displaystyle \scriptstyle x_{n}}$為第n個取樣點，則函式${\displaystyle \scriptstyle x(t)}$可以表示為：

${\displaystyle x(t)=\sum _{n=-\infty }^{\infty }x_{n}{\sin \pi (2Bt-n) \over \pi (2Bt-n)}.\,}$

和其他證明類似，此處假設原函式的傅立葉變換存在，因此證明中沒有說明採樣定理是否可以延伸到有限頻寬的固定隨機過程。

腳註

1. 實際的係數包括一個係數${\displaystyle \scriptstyle 1/2B=T.}$，因此香農係數為${\displaystyle \scriptstyle T\cdot x(nT)}$，和Eq.1相符。

在多變數訊號及圖形上的應用

圖6：取樣不足的圖，會出現莫列波紋

圖7

取樣定理常表示為單一變數的函式，因此定理可以直接應用到和時間相關的一維訊號。不過取樣定理可以直接延伸到任意數量變數的函式。例如像灰階影像常表示為二維的實數陣列（或是矩陣），其中的實數表示在對應行及列的取樣位置下，像素的相對強度。因此圖案會需要二個獨立的變數來表示其位置，一個表示對應的行，一個表示對應的列。

彩色影像一般會包括三個獨立的灰階值，分別表示紅色、綠色及藍色等三原色（三原色光模式，簡稱RGB）的強度。其他用三個元素的向量表示一個點的顏色空間有HSL和HSV色彩空間、CIELAB及XYZ等。而像CMYK則是用淺藍色、紫紅色、黃色及黑色的強度來表示。這些色彩空間都是二維空間上的向量值函式。

和一維離散訊號的情形類似，若圖形的採樣解析度（或是像素密度）不適當，可能會有混疊的情形。例如密條紋襯衫若是用的數值若是用數位相機的圖像感測器取樣時，可能會造成混疊，這種二維的混疊會形成莫列波紋，改善方式是提高空間的取樣率，例如拍照時更靠近襯衫，用高解析度的感測器，或是在取樣前先進行光學模糊處理。

另一個例子是右邊的方格條紋，上方的圖是不滿足取樣定理下的訊號。下方則是先經過低通濾波器再降取樣，得到一個較小，但沒有莫列波紋。上圖則是直接降取樣，沒有先經過低通處理後的圖。

取樣定理在影像上的應用需小心的進行。例如相機中標準影像感測器（CCD或CMOS）的取樣程式和理想的取樣程式有相當的差距，理想的取樣程式會在一個點量測其影像強度，但影像感測器中為了獲得足夠的光量，其感測影像的區域較。換句話說，感測器是一個有限寬度的點擴散函式。一般而言這類感測器采樣到的類比光學資訊不是有限頻寬的，而不理想的采樣本身即為低通濾波器，不過不一定可以移除會造成混疊的高頻雜訊。若取樣區域（感測器大小）沒有大到可以有反鋸齒效果時，一般會需要獨立的反鋸齒濾鏡（光學低通濾鏡）來使影像模糊。雖然影像有這些和采樣定理有關的問題，不過采樣定理可以描述提升取樣及減取樣的基礎。

圖8：一組在臨界頻率的弦波，採樣時都是反覆出現的+1和–1，他們都是彼此的混疊訊號，甚至其頻率還沒超過取樣頻率的一半

臨界頻率

為了描述f_s > 2B的必要性，考慮右圖（圖8）中的一組弦波，公式如下，但θ值各有不同：

${\displaystyle x(t)={\frac {\cos(2\pi Bt+\theta )}{\cos(\theta )}}\ =\ \cos(2\pi Bt)-\sin(2\pi Bt)\tan(\theta ),\quad -\pi /2<\theta <\pi /2.}$

其中f_s = 2B或是可以寫為T = 1/(2B)，採樣值為：

${\displaystyle x(nT)=\cos(\pi n)-\underbrace {\sin(\pi n)} _{0}\tan(\theta )=(-1)^{n}}$

和θ值無關。上述的歧義是采樣定理中使用嚴格的不等式，不允許等式的原因。

對於非基頻訊號的取樣

香農曾提到^[2]：

若頻帶的最小值不是零，而是由其他較大的值，也可以產生類似的結果，可以用線性轉換（對應物理上的單邊帶調變）到最小值為零的頻帶來證明。此例中基本脈波是單邊帶調變下的sin(x)/x。

因此這是一個針對沒有基頻成份訊號（其頻帶有一部份的訊號非零，但此寬度又和最大頻率無關）進行取樣的充份條件。

帶通條件為X(f) = 0，針對在所有在開區域範圍以外的非負f：

${\displaystyle \left({\frac {N}{2}}f_{\mathrm {s} },{\frac {N+1}{2}}f_{\mathrm {s} }\right),}$

針對某非負整數N。此公式包括一般的基頻條件，N=0。

對應的內插函式為理想Sinc帶通濾波器的脈衝響應，（而不是之前用的理想Sinc低通濾波器），會切掉頻帶的上方及下方，這也是一組低通濾波器脈衝響應的差：

${\displaystyle (N+1)\,\operatorname {sinc} \left({\frac {(N+1)t}{T}}\right)-N\,\operatorname {sinc} \left({\frac {Nt}{T}}\right).}$

其他的推廣，例如訊號在數個不連續的頻帶，也是可行的。甚至是最廣義的取樣定理也不一定有一個可能正確的反例。也就是說無法確定是否只要不滿足取樣定理，就一定會有訊號的喪失。不過以工程的角度來看，比較保守的作法是假設若不滿足取樣定理，就很可能會有訊號的喪失。

非均勻採樣

香農的取樣定理可以延伸到非均勻採樣，也就是採樣的時間間隔非一定值。非均勻採樣的取樣定理指出針對band-limited的訊號，只要平均採樣頻率滿足奈奎斯特條件，就可以從採樣訊號完整重建原始訊號^[4]。因此雖然均勻採樣在訊號重建的演算法上比較簡單，但這不是完整重建的必要條件。

非基頻及非均勻採樣的泛用理論是在1967年由亨利·藍道提出^[5]。簡單的說，藍道證明了平均取樣率至少需要是訊號佔據頻寬的二倍，但前提是已知訊號的頻譜及其佔據的頻寬。 在1990年代末期，此研究已延伸到訊號佔據頻寬的數量已知，但實際在頻譜上位置未知的情形^[6]。在2000年代已利用壓縮感知發展了一個完整的理論。此理論用訊號處理的語言寫成，在2009年的論文中發表^[7]。論文中證明，若頻率的位置未知，則取樣頻率需至少為奈奎斯特準則的二倍。換句話說，因為不知道光學頻譜的位置，需要將取樣頻率乘二為代價。注意此最小取樣頻率的要求不一定保證其數值穩定性。

欠取樣

當一個訊號被欠取樣（英語：Undersampling）時，必須滿足取樣定理以避免混疊。為了滿足取樣定理的要求，訊號在進行減取樣操作前，必須通過一個具有適當截止頻率的低通濾波器。這個用於避免混疊的低通濾波器，稱為抗混疊濾波器。

在奈奎斯特速率以下，有額外限制條件的取樣

奈奎斯特–夏農取樣定理是對於帶限函式取樣及重建的充分條件。若是用惠特克–夏農內插公式（英語：Whittaker–Shannon interpolation formula）重建原訊號，奈奎斯特準則也是避免混疊的必要條件，因為若採樣速率小於訊號頻帶限制的二倍，可能有些訊號無法正確重建。不過若訊號有其他的限制，則奈奎斯特準則就不是混疊的必要條件了。

像近來在進行研究的壓縮感知就是一個利用對訊號額外假設來進行壓縮的例子，壓縮感知可以用奈奎斯特速率要慢的速率採樣，然後可以完整的重建原訊號。這特別用在訊號在一些層面較稀疏（或可壓縮）的情形。像壓縮感知可以處理有效頻寬（EB)）很低，但不確定其頻率分佈位置的訊號（此時取樣定理就不適用了）。換句話說，其頻譜較稀疏。若用取樣定理，最小的採樣速率是2B，若是用壓縮感知，採樣速率若略低於2EB，仍可以完整的重建。不過此作法的重建已不再是用公式處理，而是要求解凸優化，需要有良好研究，而可能是非線性的方式處理。

歷史背景

哈里·奈奎斯特1928年的論文《Certain topics in telegraph transmission theory》中就已隱含了取樣定理，他證明了一個頻寬為B的系統可以傳送最多2B個獨立的脈波，不過他沒有直接處理連續訊號取樣及重建的問題。同一時期的卡爾·庫普夫米勒（英語：Karl Küpfmüller）證明了類似的結果^[8]，也討論到頻帶限制濾波器的sinc函式脈衝響應，以及其積分，步階響應的三角積分，頻帶限制濾波器及訊號重建濾波器是採樣定理的核心，因此在一些地區會將這二個濾波器稱為Küpfmüller filter。

取樣定理是在夏農在1949年《Communication in the presence of noise》中提出。之前相關的研究有V. A. Kotelnikov（英語：弗拉基米爾·科捷利尼科夫）在1933年《在電纜及"以太"中電子通訊的傳輸能力》（翻譯自俄文），以及數學家埃德蒙·泰勒·惠特克在1915年的《Expansions of the Interpolation-Theory》（Theorie der Kardinalfunktionen）、J. M. Whittaker在1935年的《Interpolatory function theory》以及丹尼斯·加博爾1946年提出的《Theory of communication》。1999年時愛德華萊茵基金會（英語：Eduard Rhein Foundation）給予科捷利尼科夫基礎研究獎，原因是「第一位提出理論正確的採樣定理」^[9]。

相關條目

• 巴里安-羅定理（英語：Balian–Low theorem），類似的取樣頻率理論下限，但應用在時分頻析中。
• 張-馬克斯定理（英語：Cheung–Marks theorem）說明何時依取樣定理重建的訊號會是病態的。
• 夏農定理
• 奈奎斯特ISI判準（英語：Nyquist ISI criterion）
• 零交越重建（英語：Reconstruction from zero crossings）
• 零階保持器（英語：Zero-order hold）

參考資料

1. John J. Benedetto, Paulo J. S. G. Ferreira (編). Modern Sampling Theory: Mathematics and Applications. Applied and Numerical Harmonic Analysis. Boston, MA, USA: Birkhäuser. 2001. ISBN 978-0-8176-4023-1 （英語）.
2. , "Communication in the presence of noise", Proc. Institute of Radio Engineers, vol. 37, no. 1, pp. 10–21, Jan. 1949. Reprint as classic paper in: Proc. IEEE, vol. 86, no. 2, (Feb. 1998) 網際網路檔案館的存檔，存檔日期2010-02-08.
3. sinc函式依照傅立葉轉換表的202行及102行
4. Nonuniform Sampling, Theory and Practice (ed. F. Marvasti), Kluwer Academic/Plenum Publishers, New York, 2000
5. Landau, H. J. Necessary density conditions for sampling and interpolation of certain entire functions. Acta Math. 1967, 117 (1): 37–52. doi:10.1007/BF02395039.
6. see, e.g., Feng, P. Universal minimum-rate sampling and spectrum-blind reconstruction for multiband signals. Ph.D. dissertation, University of Illinois at Urbana-Champaign. 1997.
7. Mishali, Moshe; Eldar, Yonina C. Blind Multiband Signal Reconstruction: Compressed Sensing for Analog Signals. IEEE Trans. Signal Processing. March 2009, 57 (3). CiteSeerX: 10.1.1.154.4255.
8. Küpfmüller, Karl. Über die Dynamik der selbsttätigen Verstärkungsregler. Elektrische Nachrichtentechnik. 1928, 5 (11): 459–467 （德語）. (English translation 2005) （頁面存檔備份，存於網際網路檔案館）.
9. Basic Research Award 1999 網際網路檔案館的存檔，存檔日期2015-02-02.

• E. T. Whittaker, "On the Functions Which are Represented by the Expansions of the Interpolation Theory," Proc. Royal Soc. Edinburgh, Sec. A, vol.35, pp.181-194, 1915
• H. Nyquist, "Certain topics in telegraph transmission theory," Trans. AIEE, vol. 47, pp. 617-644, Apr. 1928.
• V. A. Kotelnikov, "On the carrying capacity of the ether and wire in telecommunications," Material for the First All-Union Conference on Questions of Communication, Izd. Red. Upr. Svyazi RKKA, Moscow, 1933 (Russian).
• C. E. Shannon, "Communication in the presence of noise", Proc. Institute of Radio Engineers, vol. 37, no.1, pp. 10-21, Jan. 1949.
• J. R. Higgins: Five short stories about the cardinal series, Bulletin of the AMS 12(1985)
• V. A. Kotelnikov, "On the carrying capacity of the ether and wire in telecommunications", Material for the First All-Union Conference on Questions of Communication, Izd. Red. Upr. Svyazi RKKA, Moscow, 1933 (Russian). (english translation, PDF) （頁面存檔備份，存於網際網路檔案館）
• Karl Küpfmüller, "Utjämningsförlopp inom Telegraf- och Telefontekniken", ("Transients in telegraph and telephone engineering"), Teknisk Tidskrift, no. 9 pp. 153–160 and 10 pp. 178–182, 1931. [1] （頁面存檔備份，存於網際網路檔案館） [2] （頁面存檔備份，存於網際網路檔案館）
• R.J. Marks II: Introduction to Shannon Sampling and Interpolation Theory （頁面存檔備份，存於網際網路檔案館）, Spinger-Verlag, 1991.
• R.J. Marks II, Editor: Advanced Topics in Shannon Sampling and Interpolation Theory （頁面存檔備份，存於網際網路檔案館）, Springer-Verlag, 1993.
• R.J. Marks II, Handbook of Fourier Analysis and Its Applications, Oxford University Press, (2009), Chapters 5-8. Google books （頁面存檔備份，存於網際網路檔案館）.
• H. Nyquist, "Certain topics in telegraph transmission theory", Trans. AIEE, vol. 47, pp. 617–644, Apr. 1928 Reprint as classic paper in: Proc. IEEE, Vol. 90, No. 2, Feb 2002.
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP, Section 13.11. Numerical Use of the Sampling Theorem, Numerical Recipes: The Art of Scientific Computing 3rd, New York: Cambridge University Press, 2007 [2016-03-16], ISBN 978-0-521-88068-8, （原始內容存檔於2011-08-11）
• C. E. Shannon, "Communication in the presence of noise", Proc. Institute of Radio Engineers, vol. 37, no.1, pp. 10–21, Jan. 1949. Reprint as classic paper in: Proc. IEEE, Vol. 86, No. 2, (Feb 1998)
• Michael Unser: Sampling-50 Years after Shannon （頁面存檔備份，存於網際網路檔案館）, Proc. IEEE, vol. 88, no. 4, pp. 569–587, April 2000
• E. T. Whittaker, "On the Functions Which are Represented by the Expansions of the Interpolation Theory", Proc. Royal Soc. Edinburgh, Sec. A, vol.35, pp. 181–194, 1915
• J. M. Whittaker, Interpolatory Function Theory, Cambridge Univ. Press, Cambridge, England, 1935.

外部連結

• Learning by Simulations （頁面存檔備份，存於網際網路檔案館） Interactive simulation of the effects of inadequate sampling
• Interactive presentation of the sampling and reconstruction in a web-demo Institute of Telecommunications, University of Stuttgart
• Undersampling and an application of it （頁面存檔備份，存於網際網路檔案館）
• Sampling Theory For Digital Audio
• Journal devoted to Sampling Theory （頁面存檔備份，存於網際網路檔案館）
• Sampling Theorem with Constant Amplitude Variable Width Pulse （頁面存檔備份，存於網際網路檔案館）
• "The Origins of the Sampling Theorem" by Hans Dieter Lüke published in "IEEE Communications Magazine" April 1999. CiteSeerX: 10.1.1.163.2887.