0.999…

0.999…，也可寫作${\displaystyle 0.{\overline {9}}}$、${\displaystyle 0.{\dot {9}}}$或是${\displaystyle 0.(9)}$，是一個具有特殊意義的無限循環小數，由小數點後無限的 9 序列組成。在數學的完備實數系中，「0.999…」所表示的數與「1」相同。^[1]換句話說，「0.999...」不是「幾乎完全」或「非常、非常接近但不完全」等於1；相反，「0.999...」和「1」正好代表相同的數字。

一個立體化的0.999…文本。

有很多方法可以證明這種等式，從直覺的論證到嚴謹的數學證明。 所使用的技術取決於目標受眾、背景假設、歷史背景和實數概念的發展，因為通常是在實數系統中定義 0.999...。 在其他系統中，0.999... 可以具有相同的含義、不同的定義或未定義。

一般地說，每個非零有限小數都有兩個相等的表示形式（例如，8.32 和 8.31999...），這是所有位置數字系統表示形式的屬性，無論基數如何。 對有限小數十進制表示形式的功利主義偏好導致了一種誤解，認為它是唯一的表示形式。 由於這個原因和其他原因（例如依賴於非基本技術、屬性或學科的嚴格證明），有些人可能會發現等式足夠違反直覺，從而質疑或拒絕它，而這一直是數學教育中多項研究的主題。

簡介

0.999…是書寫於小數記數系統中的一個數，讀作：「零點九，九循環」。一些最簡單的0.999… = 1 的證明都依賴於這個系統方便的算術性質。大多數的小數算術──加法、減法、乘法、除法，以及大小的比較，使用與整數差不多的數位層次的操作。與整數一樣，任何兩個有限小數只要數位不同，那麼數值也一定不同。相對的，任何一個形如0.99…9的數，但是9的數量有限，則這個數字是小於1的。

這類展開式的非唯一性不僅限於十進制系統，相同的現象也出現在其它的整數進位制中。數學家們也列舉出了一些1在非整數進位制中的寫法，這種現象也不是僅僅限於1的：對於每一個非零的有限小數，都存在另一種含有無窮多個9的寫法，由於簡便的原因，這時幾乎肯定使用有限小數的寫法，這樣就更加使人們誤以為沒有其它寫法了，實際上，一旦在完備實數系中允許使用無限小數，那麼在所有的進位制中都有無窮多種替代的寫法，例如，18.3287與18.3286999…、18.3287000…，以及許多其它的寫法，都表示相同的數，這些各種各樣的等式被用來更好地理解分數的小數展開式的規律，以及一個簡單碎形圖形──康托爾集合的結構，它們也出現在一個對整個實數的無窮集合的古典研究之中。

在過去數十年裡，許多數學教育的研究人員研究了大眾及學生們對該等式的接受程度，許多學生在學習開始時懷疑甚至拒絕該等式，但許多學生被老師、教科書和如下章節的算術推論說服並接受兩者是相等的。儘管如此，許多人們仍常感到懷疑，及提出進一步的辯解，這經常是由於存在不少對數學實數的錯誤觀念等背後因素（參見以下教育中遇到的懷疑一章節），例如認為每一個實數都有唯一的一個小數展開式，以及認為無限小（無窮小）不等於0，並且將0.999…視為一個不定值，即該值只是一直微微擴張變大，因此與1的差永遠是無限小而不是0，因此「永遠都差一點」。可以構造出符合這些直觀的數系，但這個觀念只能用於初等數學或多數更高等數學中的標準實數系統之外進行，的確，某些設計含有「恰恰小於1」的數，不過，這些數一般與0.999…無關（因為與之相關的理論上和實踐上都皆無實質用途），但在數學分析中引起了相當大的關注。

誤解0.999…中的省略號的意義，是誤解0.999…= 1的其中一個原因。這裡省略號的用法與日常語言中0.99…9的用法是不同的，0.99…9中的省略號意味著的有限的部分被省略掉了。但是，當用來表示一個循環小數的時候，"…"則意味著無限的部分被省略掉了，這只能用極限的數學概念來闡釋。作為使用傳統數學的結果，指派給記數表示式「0.999…」的值定義為一個實數，該實數為收斂數列（0.9，0.99，0.999，0.9999，0.99999，…）的極限。「0.999…」是一個數列的極限，從而，對於0.999…= 1這個等式就很直觀了。

與整數和有限小數的情況不一樣，其實記數法也可以用多種方式表示單一個數值。例如，如果使用分數，${\displaystyle {\begin{smallmatrix}{\frac {1}{3}}={\frac {2}{6}}\end{smallmatrix}}}$。但是，一個數最多只能用兩種無限小數的方法來表示。如果有兩種方法，那麼其中一種一定是從某一位開始全是循環重複的9，而另外一種則是從某一位開始就全是循環重複的0。

0.999… = 1 有許多證明，它們各有不同的嚴謹性，一個嚴謹的證明可以簡單地說明：考慮到兩個實數其實是同一個的，若且唯若它們的差等於零。大部分人都同意；0.999…與 1 的差，就算存在也是非常的小(實際上根本不存在，即差等於0)。考慮到以上的收斂數列，這時可以證明這個差的大小一定是小於任何一個正數的，也可以證明（詳細內容參見阿基米德性質），唯一具有這個性質的實數是0。由於差是0，可知 1 和 0.999…是同一數，用相同的理由，也可以解釋為什麼「0.333…=1/3」；以及該等式乘上3倍後可得出「0.999… = 1」。

證明

對位相減

在不考慮柯西序列的情況下：1.00000…−0.99999…這個結果為0.000…，也就是後面的0無限循環。這兩個數目皆可表示成無限循環小數，小數點後五位之後還會一直填上0，始終無法找到最後一位來填上1，因為如果補上1就會成為有限小數。1.000… - 0.999… = 0.000… = 0，故1 = 0.999…。

這假設了0.999…沒有「最後的9」、這些無限循環小數的小數點後的位數為可列的（可以由第一個數位一個位一個位數下去而於有限次數到任一個數位）（這已得出0.999…沒有「最後的9」）、1.000… - 0.999…的結果存在小數表示式。運算結果將沒有「最後的1」，所以1與0.999…沒有差值。

代數

分數

無限小數是有限小數的一個必要的延伸，其中一個原因是用來表示分數。用長除法，一個像${\displaystyle {\begin{smallmatrix}{\frac {1}{3}}\end{smallmatrix}}}$的簡單整數，長除法後變成了一個循環小數0.333…，其中有無窮多個數字3。利用這個小數，很快就能得到一個 0.999… = 1 的證明。用 3 乘以 0.333… 中的每一個 3，便得到 9，所以 3 × 0.333… 等於 0.999…。由於 ${\displaystyle {\begin{smallmatrix}3\times {\frac {1}{3}}\end{smallmatrix}}}$ 等於1，所以 0.999… = 1。^[2]

這個證明的另外一種形式，是用${\displaystyle {\frac {1}{9}}=0.111...}$同乘以9。

${\displaystyle {\begin{aligned}0.333\cdots &{}={\frac {1}{3}}\\3\times 0.333\cdots &{}=3\times {\frac {1}{3}}={\frac {3\times 1}{3}}\\0.999\cdots &{}=1\end{aligned}}}$

${\displaystyle {\begin{aligned}0.111\cdots &{}={\frac {1}{9}}\\9\times 0.111\cdots &{}=9\times {\frac {1}{9}}={\frac {9\times 1}{9}}\\0.999\cdots &{}=1\end{aligned}}}$

由於兩個方程都是正確的，因此根據相等關係的遞移性質，0.999…一定等於1。類似地，${\displaystyle {\begin{smallmatrix}{\frac {3}{3}}=1\end{smallmatrix}}}$，且${\displaystyle {\begin{smallmatrix}{\frac {3}{3}}=0.999\ldots \end{smallmatrix}}}$。所以0.999…= 1。

一個特別的除法豎式

用豎式計算可得 ${\displaystyle {\frac {8.999...}{9}}=0.999...}$

設 ${\displaystyle n=0.999...\quad }$

則

${\displaystyle {\begin{aligned}{\frac {8+n}{9}}&=n\\8+n&=9n\\\end{aligned}}}$

解此一元一次方程式得:

${\displaystyle {\begin{aligned}8&=8n\\n&=1\\\end{aligned}}}$

所以 ${\displaystyle 0.999...=n=1\quad }$ 。

位數操作

另外一種證明更加適用於其它循環小數。當一個小數乘以10時，其數字不變，但小數點向右移了一位。因此10 × 0.999…等於9.999…，它比原來的數大9。

考慮從9.999…減去0.999…。這時可以一位一位地減；在小數點後的每一位，結果都是9 - 9，也就是0。但末尾的零並不能改變一個數，所以相差精確地是9。最後一個步驟用到了代數。設0.999… = c，則10c − c = 9，也就是9c = 9。等式兩端同除以9，便得證：c = 1。^[2]用一系列方程來表示，就是

0.(9)=1的解釋

${\displaystyle {\begin{aligned}c&=0.999\ldots \\10c&=9.999\ldots \\10c-c&=9.999\ldots -0.999\ldots \\9c&=9\\c&=1\\0.999\ldots &=1\end{aligned}}}$

以上兩個證明中的位數操作的正確性，並不需要盲目相信，也無需視為公理；它是從小數和所表示的數之間的基本關係得出的。這個關係，可以用幾個等價的方法來表示，已經規定了0.999…和1都表示相同的實數。

實分析

無窮級數和數列

對於任何一個小數，都可以定義為無窮級數的和。一般地：

${\displaystyle b_{0}.b_{1}b_{2}b_{3}b_{4}\ldots =b_{0}+b_{1}({\tfrac {1}{10}})+b_{2}({\tfrac {1}{10}})^{2}+b_{3}({\tfrac {1}{10}})^{3}+b_{4}({\tfrac {1}{10}})^{4}+\cdots }$.

對於0.999…來說，這時可以使用等比級數的收斂定理：^[3]

如果${\displaystyle |r|<1}$，則${\displaystyle ar+ar^{2}+ar^{3}+\cdots ={\frac {ar}{1-r}}}$.

由於0.999…是公比為${\displaystyle r=\textstyle {\frac {1}{10}}}$的等比級數的和，應用以上定理，很快就可以得出證明了：

${\displaystyle 0.999\ldots =9({\tfrac {1}{10}})+9({\tfrac {1}{10}})^{2}+9({\tfrac {1}{10}})^{3}+\cdots ={\frac {9({\tfrac {1}{10}})}{1-{\tfrac {1}{10}}}}=1}$，

這個證明（實際上是10等於9.999…）早在1770年就在瑞士數學家萊昂哈德·歐拉的作品《Elements of Algebra》（《代數的要素》）中出現了。^[4]

四進制的小數數列（0.3，0.33，0.333，……）收斂於1。

等比級數的和本身，是一個比歐拉還要早的結果。一個典型的18世紀的推導用到了逐項的操作，類似於以上的代數證明。直到1811年，Bonnycastle的教科書《An Introduction to Algebra》（《代數的介紹》）依然使用這種等比級數的方法來證明對0.999…使用的策略是正當的。^[5]在19世紀，這種在當時被以為隨隨便便的求和方法遭到了反對，這樣便導致了現在仍然占有支配地位的定義：一個級數的和定義為數列的部分和的極限。該定理的一個對應的證明，明確地把這個數列計算出來了；這可以在任何一本以證明為基礎的微積分或數學分析的教科書中找到。^[6]

對於數列（x₀，x₁，x₂，…）來說，如果當n增大時，距離|x − x_n|變得任意地小，那麼這個數列就具有極限x。0.999… = 1的表述，可以用極限的概念來闡釋和證明：

${\displaystyle 0.999\ldots =\lim _{n\to \infty }0.\underbrace {99\ldots 9} _{n}=\lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1.\,}$^[7]

最後一個步驟—lim ¹/_10ⁿ = 0—通常由實數擁有阿基米德性質這一原理來證明。這個以極限為基礎的對0.999…的看法，有時會用比較引人注意但不太精確的話語來表達。例如，在1846年的美國教科書《大學算術》（《The University Arithmetic》）中有這麼一句：「0.999+，到無窮遠處等於1，這是因為每加上一個9，都會使它的值更加接近於1」（.999 +, continued to infinity = 1, because every annexation of a 9 brings the value closer to 1）；在1895年的美國教科書《Arithmetic for Schools》（《學校算術》）中也有：「…如果有非常多的9，那麼1和0.99999…的差就小得難以想像了」（「…when a large number of 9s is taken, the difference between 1 and .99999…becomes inconceivably small」）。^[8]這種啟發式的教學法，常常被學生們誤解為0.999…本身就小於1。

區間套和最小上界

參見：區間套

區間套：在三進制中，1 = 1.000… = 0.222…

以上的級數定義，是一個用小數展開式來定義實數的簡單的方法。還有一種補充的方法，是相反的過程：對於一個給定的實數，定義一個相關的小數展開式。

如果知道一個實數x位於閉區間[0, 10]內（也就是說，這個實數大於或等於0，而小於或等於10），這時就可以想像把這個區間分成十個部分，只在終點處相重疊：[0, 1]、[1, 2]、[2, 3]，依此類推，直到[9, 10]。實數x一定是屬於這十個區間的一個；如果它屬於[2, 3]，這時就把數字「2」記錄下來，並把這個區間再細分成十個子區間：[2, 2.1]、[2.1, 2.2]、…、[2.8, 2.9]、[2.9, 3]。把這個過程一直繼續下去，這時便得到了一個無窮的區間套序列，由無窮個數字b₀、b₁、b₂、b₃、…來標示，並記

x = b₀.b₁b₂b₃…

在這種形式中，1 = 1.000…而且1 = 0.999…的事實，反映了1既位於[0, 1]，又位於[1, 2]，所以這時在尋找它的數字時，可以選擇任意一個子區間。為了保證這種記法沒有濫用「=」號，這時需要一種辦法來為每一個小數重新構造一個唯一的實數。這可以用極限來實現，但是還有其它的方法。^[9]

一個簡單的選擇，是區間套定理，它保證只要給出了一個長度趨近於零的閉區間套序列，那麼這些區間套的交集就正好是一個實數。這樣，b₀.b₁b₂b₃…便定義為包含在所有的區間[b₀, b₀ + 1]、[b₀.b₁, b₀.b₁ + 0.1]，依此類推的唯一的實數。而0.999…就是位於所有的區間[0, 1]、[0.9, 1]、[0.99, 1]、[0.99…9, 1]（對於任意有限個9）的唯一的實數。由於1是所有這些區間的公共元素，因此0.999… = 1。^[10]

區間套定理通常是建立在一個更加基本的實數特徵之上的：最小上界的存在。為了直接利用這些事物，這時可以把b₀.b₁b₂b₃…定義為集合{b₀，b₀.b₁，b₀.b₁b₂，…}的最小上界。^[11]然後這時就可以證明，這種定義（或區間套的定義）與劃分的過程是一致的，再一次證明了0.999… = 1。湯姆·阿波斯托爾得出結論：

“

一個實數可以有兩種不同的小數表示法，僅僅是兩個不同的實數集合可以有相同的最小上界的一個反映。 (The fact that a real number might have two different decimal representations is merely a reflection of the fact that two different sets of real numbers can have the same supremum.) [12]

”

從建構實數著手

參見：實數的結構

有些方法用公理集合論明確把實數定義為一定的建立在有理數上的結構。自然數──0、1、2、3，依此類推──從零開始並繼續增加，這樣每一個自然數都有一個後繼者。這時可以把自然數的概念延伸到負數，得出所有的整數，並可以進一步延伸到比例，得出所有的有理數。這些數系伴隨著加法、減法、乘法和除法的算術。更加微妙地，它們還包括排序，這樣一個數就可以與另一個進行比較，並發現是大於、小於，還是等於。

從有理數到實數的一步，是一個很大的延伸。至少有兩種常見的方法來達到這一步，它們都在1872年出版：戴德金分割，以及柯西序列。直接用到這些結構的0.999… = 1的證明，現在已經無法在實分析的教科書中找到了；最近幾個年代的趨勢，是使用公理化的分析。即使提供了這樣的一個結構，它也通常被用來證明實數的公理，從而為以上的證明提供證據。然而，有些作者表達了從一個結構開始才是邏輯上更恰當的想法，這樣得出的證明就更加完備了。^[13]

戴德金分割

主條目：戴德金分割

在戴德金分割的方法中，每一個實數x定義為所有小於x的有理數所組成的無窮集合。^[14]比如說，實數1就是所有小於1的有理數的集合。^[15]每一個正的小數展開式很容易決定了一個戴德金分割：小於某個展開階段的有理數的集合。所以實數0.999…是有理數r的集合，使得r < 0，或r < 0.9，或r < 0.99，或r小於其它具有 ${\displaystyle {\begin{smallmatrix}1-{\big (}{\tfrac {1}{10}}{\big )}^{n}\end{smallmatrix}}}$ 形式的數。^[16]0.999…的每一個元素都小於1，因此它是實數1的一個元素。反過來，1的一個元素是有理數 ${\displaystyle {\begin{smallmatrix}{\tfrac {a}{b}}<1\end{smallmatrix}}}$，也就是${\displaystyle {\begin{smallmatrix}{\tfrac {a}{b}}<1-{\big (}{\tfrac {1}{10}}{\big )}^{b}\end{smallmatrix}}}$。由於0.999…和1包含相同的有理數，因此它們是相同的集合：0.999… = 1。

把實數定義為戴德金分割，首先由理察·戴德金在1872年出版。^[17] 以上把每一個小數展開式分配一個實數的方法，應歸於弗雷德·里奇曼在《Mathematics Magazine》（《數學雜誌》）上發表的一篇名為「Is 0.999… = 1?」（「0.999… = 1嗎？」）的演講稿，主要是為大學的數學教師，尤其是初級／高級程度，以及他們的學生而作。^[18]里奇曼注意到，在有理數的任何一個稠密子集中取戴德金分割，都得到相同的結果；特別地，他用到了十進分數（分母為10的冪的分數），這樣便更快得出證明了：「所以，這時看到，在實數的傳統定義中，方程 0.9* = 1 在一開始就建立了。」^[19]把這個步驟再作進一步的修改，便得到了另外一個結構，里奇曼對描述這個結構更感興趣；參見以下的「其它數系」。

柯西序列

主條目：柯西序列

另外一種構造實數的方法，間接地用到了有理數的排序。首先，有理數x和y之間的距離定義為絕對值|x − y|，其中絕對值|z|定義為z和−z的最大值，因此總是非負的。這樣實數便被定義為關於這個距離的具有柯西序列性質的有理數序列。也就是說，每一個實數都是一個柯西收斂的數列（x₀，x₁，x₂，…）。這是一個從自然數到有理數的映射，使得對於任何正有理數δ，總存在一個N，使得對於所有的m、n > N，都有|x_m − x_n| ≤ δ。（兩項之間的距離變得比任何正的有理數都要小。）^[20]

如果（x_n）和（y_n）是兩個柯西數列，那麼如果數列（x_n − y_n）有極限0，這兩個數列便定義為相等的。把小數b₀.b₁b₂b₃…拆開來，便得到了一個有理數序列，它是柯西序列；這個序列對應的實數被定義為這個小數的值。^[21]所以，在這種形式中，這時的任務就是要證明，有理數序列

${\displaystyle \left(1-0,1-{9 \over 10},1-{99 \over 100},\cdots \right)=\left(1,{1 \over 10},{1 \over 100},\cdots \right)}$

有極限0。對於n = 0、1、2、…，考慮數列的第n項，這時需要證明

${\displaystyle \lim _{n\rightarrow \infty }{\frac {1}{10^{n}}}=0}$。

這個極限是眾所周知的；^[22]一個可能的證明，是在數列的極限的定義中，對於ε = a/b > 0，這時可以取N = b。所以，這又一次證明了0.999… = 1。

把實數定義為柯西序列，首先由愛德華·海涅和格奧爾格·康托爾獨立發表，也是在1872年。^[17]以上的小數展開式的方法，包括0.999… = 1的證明，則主要是得自格利菲斯（Griffiths）和希爾頓（Hilton）在1970年的作品《一本經典數學的綜合教科書：一個當代的闡釋》（A comprehensive textbook of classical mathematics: A contemporary interpretation）。這本書是特別為了以當代的眼光回顧一些熟悉的數學概念而作的。^[23]

推廣

0.999… = 1的證明，立刻可以進行兩種推廣。首先，對於每一個非零的有限小數（也就是說，從某一位開始全是零），都存在另外一個與其相等的數，從某一位開始全是9。例如，0.24999…等於0.25，就像這時考慮的特殊情況。這些數正好是十進分數，而且是稠密的。^[24]

其次，一個類似的定理可以應用到任何一個底數或進位制。例如，在二進制中，0.111…等於1；而在三進制中，0.222…等於1。實分析的教科書很有可能略過0.999…的特殊情況，而從一開始就介紹這兩種推廣的一種或兩種。^[25]

1的其它表示法也出現在非整數進位制中。例如，在黃金進制中，兩個標準的表示法就是1.000…和0.101010…，此外還有無窮多種含有相鄰的1的表示法，如0.11，0.1011，0.101011等等。一般地，對於幾乎所有的1和2之間的q，在q進制中都有無窮多種1的展開式。而另一方面，依然存在不可數個q（包括所有大於1的自然數），使得在q進制中只有一種1的展開式，除了顯然的1.000…。這個結果首先由保羅·埃爾德什、Miklos Horváth和István Joó在大約1990年獲得。1998年，Vilmos Komornik和Paola Loreti確定了具有這種性質的最小的進位制──Komornik-Loreti常數q = 1.787231650…。在這個進位制中，1 = 0.11010011001011010010110011010011…；其數字由圖厄-摩斯數列給出，不是循環小數。^[26]

一個更加深遠的推廣，提到了最一般的進位制。在這些進位制中，一個數也有多種表示法，在某種意義上來說難度甚至更大。例如：^[27]

• 在平衡三進制系統中，¹/₂ = 0.111… = 1.111…。
• 在階乘進位制系統中，1 = 1.000… = 0.1234…。

Marko Petkovšek證明了這種歧義是使用進位制的必然結果：對於任何一個把所有實數命名的系統，總有無窮多個實數有多種表示法，而這些實數所組成的集合又是稠密的。他把這個證明稱為「一個基本點集拓撲學的指導性的練習」：它包含了把各位數的集合視為斯通空間，並注意到它們的實數表示法可以由連續函數給出。^[28]

應用

0.999…的其中一個應用，出現在基本數論中。1802年，H·古得溫出版了一份觀察資料，描述了分母為一定的素數的分數的小數展開式中9的出現。例子包括：

• ¹/₇ = 0.142857142857…，而142 + 857 = 999。
• ¹/₇₃ = 0.0136986301369863…，而0136 + 9863 = 9999。

E·米迪在1836年證明了關於這類分數的一個一般的結果，現在稱為米迪定理。當初出版時沒有寫得很清楚，這時也不知道他的證明是不是直接提到了0.999…，但至少有一個W·G·萊維特的現代證明是這樣的。如果這時可以證明，一個具有形式0.b₁b₂b₃…的小數是正整數，那麼它就一定是0.999…，這也就是定理中9的來源。^[29]在這個方向上繼續做研究，就可以得出諸如最大公因子、同餘、費馬素數、群元素的階，以及二次互反律等概念。^[30]

康托爾集合中¹/₄、²/₃，和1的位置。

回到實分析的主題上，三進制中的類似等式0.222… = 1在刻劃康托爾集合──一個最簡單的碎形的特徵中，扮演了一個十分重要的角色：

• 一個單位區間中的點位於康托爾集合內，若且唯若它在三進制中可以只用數字0和2來表示。

小數中的第n位反映了在第n個階段時點的位置。例如，點²⁄₃可以如常地表示為0.2或0.2000…，這是因為它位於第一個刪除部分的右面，以及以後所有的刪除部分的左面。點¹⁄₃則不表示為0.1，而表示為0.0222…，這是因為它位於第一個刪除部分的左面，以及以後所有的刪除部分的右面。^[31]

重複的9還出現在另外一個康托爾的研究成果中。在應用他在1891年發表的對角線論證法來證明單位區間的不可數性時，必須要考慮到這種因素。這種證明需要根據小數展開式來斷言兩個實數是不同的，所以這時需要避免諸如0.2和0.1999…之類的數對。一個簡單的方法把所有的實數表示為無限小數；相反的方法便排除了重複的9的可能性。^[32]一個可能更加接近於康托爾原先的證明的變體，實際上使用了二進制，把三進制展開式轉換為二進制展開式，這時也可以證明康托爾集合的不可數性。^[33]

教育中遇到的懷疑

許多學習數學的學生往往懷疑、難以接受0.999… = 1的等式，其原因有很多，從根本不相同的外觀，到對數列極限概念的深度疑慮，乃至對無限（無窮）的本性的異議，以及不少對數學錯誤的觀念等背後的因素，從而造成了這種混淆；

• 學生根據以往學習數的大小比較時使用「高位比較，相同再比次高位」的方式，個位 ${\displaystyle 0<1}$，導致拒絕承認${\displaystyle 0.{\bar {9}}=1}$。
• 許多學生認為無窮小不等於0，並且將0.999…視為一個不定值，即該值只是朝著1的方向無限地擴大，因此它與1的差永遠是無限小而不是零，即「永遠都差一點」。
• 學生們常常「堅信一個數有且僅有一種小數的表示方法」。當他們看到兩個明顯不同的小數，表示的卻是相同的實數，便認為這是一個悖論，而表面上熟悉的數1，更使這個悖論加深。^[34]
• 有些學生把「0.999…」（或類似的記法）理解為很長但有限的一串9，也許長度是可變的、未特別指出的。如果他們接受了有無窮多個9的事實，他們仍然可能認為「在無窮遠處」「有最後的一個9」。^[35]
• 直覺和模稜兩可的教導，都讓學生覺得數列的極限是一個無限的過程，而不是一個確定的值，因為一個數列不一定就有極限。如果他們明白了數列和它的極限的差別，他們就有可能把「0.999…」理解為數列，而不是它的極限。^[36]
• 有些學生相信收斂級數的值最多只是一個估計，也就是${\displaystyle 0.{\bar {9}}\approx 1}$。

這些想法在標準實數系（指具有完備性的）中都是錯誤的，但在其它數系中則有可能是正確的（要求相應數系不具備阿基米德性質，因為阿基米德性質要求數系中沒有非零無窮小^[37]）。這些系統要麼是為一般的數學用途而發明，要麼就是作為指導性的反例，使人們更好地理解0.999…。

許多這些解釋都是大衛·塔爾教授發現的，他研究了造成學生們誤解的教導方法的特徵。他訪問了他的學生以決定為什麼大多數人在一開始都拒絕接受該等式，發現「學生們仍然繼續把0.999…視為一個越來越接近1的數列，而不是一個定值，因為『你沒有指定它有多少位』或『在所有小於1的小數中，它是最大的數。』」^[38]

在所有初等的證明中，用0.333… = ¹⁄₃乘以3表面上是使學生們迫不得已接受0.999… = 1的一個成功的策略。但是，面對著對第一個等式的相信以及對第二個等式的懷疑，有些學生要麼就開始懷疑第一個等式，要麼乾脆就感到灰心喪氣了。同時也還有否認0.999…=1的學生指出1/3 比0.333…大一點（因為1/3是除不完的），所以推法「不成立」。^[39]更加複雜的方法，也不是十分有效的；有些學生完全可以應用嚴格的定義，但當他們被一個高等數學的結果，包括0.999…所震驚時，依然退回到直覺的形象上去了。例如，有一個學習實分析的學生，能夠用最小上界的定義來證明0.333… = ¹⁄₃，但仍然堅稱0.999…< 1，基於他早前對長除法的理解。^[40]其他學生也能夠證明¹⁄₃ = 0.333…，但是，面對著以上的分數證明，仍然堅稱「邏輯」能代替數學運算。

約瑟·馬祖爾講了一個故事：

“

有一個十分聰明的學習微積分的學生，他對我在課堂上講的幾乎所有內容都要提出一番異議，但對他的計算器深信不疑。

”

這位學生相信，九個數字就是學習數學所需要的一切，包括計算23的平方根。這位學生對9.99… = 10的極限證法感到彆扭，稱其為「一個難以想像的無限增長過程」。^[41]

作為埃德·杜賓斯基的數學學習的「APOS理論」的一部分，杜賓斯基和他的合作者在2005年提出：任何一個學生，只要把0.999…設想為一個有限的、不確定的數串，與1的差是無窮小，那麼他就「還沒有對無限小數形成一個完整的過程概念」。其他對0.999…有了完整的過程概念的學生，仍不一定能把這個過程「概括」成一個「對象概念」，就像他們對1的對象概念那樣，所以仍然覺得0.999…和1是不一致的。杜賓斯基還把這種概括的能力與把¹⁄₃視為一個獨立的數，以及與把實數的集合視為一個整體聯繫起來。^[42]

在大眾文化中

隨著網際網路的崛起，關於0.999…的討論已經衝出了教室，並走向了新聞群組和信息版，包括那些名義上幾乎與數學無關的信息版。在新聞群組sci.math中，辯論0.999…是一項「受歡迎的運動」，也是常見問答集之一。^[43]常見問答集涵蓋了¹⁄₃、乘以10、還有極限的證明，也間接地提到了柯西序列。

一個2003年版的報紙專欄《真實訊息（英語：The Straight Dope）》通過¹⁄₃和極限討論了0.999…，並談到了誤解：

“

我們當中的低級靈長類動物仍然在抗拒，說：0.999…其實不是表示一個數，而是表示一個過程。我們必須把那個過程停止下來，來尋找那個數，這樣0.999… = 1的等式便土崩瓦解了。真是一派胡言。 （The lower primate in us still resists, saying: .999~ doesn't really represent a number, then, but a process. To find a number we have to halt the process, at which point the .999~ = 1 thing falls apart. Nonsense.）[44]

”

（頁面存檔備份，存於網際網路檔案館）

《真實訊息》在自己的信息版引用了另外一個不明的信息版中的討論，那個信息版「大部分是關於電子遊戲的」。0.999…的問題在暴雪娛樂的Battle.net論壇的頭七年也是一個非常受歡迎的話題，以致於該公司在2004年的愚人節不得不發布了一則「新聞」，聲明0.999…就是1：

“

我們對永遠停止對這件事的討論感到十分激動。我們親眼目睹了對0.999…是否等於1的痛心和關心，並對以下的證明最終為我們的顧客解決了問題感到十分自豪。 （We are very excited to close the book on this subject once and for all. We've witnessed the heartache and concern over whether .999~ does or does not equal 1, and we're proud that the following proof finally and conclusively addresses the issue for our customers.）[45]

”

然後便提供了兩個證明，一個是極限的證明，另一個是乘以10的證明。

比較直觀的解釋，可以把一塊圓餅平均切3分來證明。

其它數系

雖然實數形成了一個非常有用的數系，把「0.999…」解釋為一個實數的決定畢竟還是一個約定，蒂莫西·高爾斯在《Mathematics: A Very Short Introduction》（《數學：一個非常簡短的介紹》）中提到，0.999… = 1的等式也是一個約定：

“

然而，這個約定決不是隨意取的，因為如果不採用這種數系，我們就被迫得要麼發明一些新奇的東西，要麼拋棄大家熟悉的算術規則。（However, it is by no means an arbitrary convention, because not adopting it forces one either to invent strange new objects or to abandon some of the familiar rules of arithmetic.）[46]

”

這時可以用不同的規則或新的事物來定義其它數系；在數系中，以上的證明便需要重新解釋。這時就有可能發現，在某一個給定的數系中，0.999…和1並不一定就是相等的。然而，許多數系都是實數系的延伸，而不是獨立的替代物，所以0.999… = 1仍然成立。就算是在這數系中，這時依然值得去檢查其它的數系，不僅僅為了知道0.999…是怎樣表現的（如果「0.999…」既有意義又不含糊），也為了知道相關現象的表現。如果這種現象與實數系統中的現象不一致的話，那麼至少一個建立在這個系統中的假設便一定不成立了。

無窮小

主條目：無窮小

0.999… = 1的證明依賴於標準實數的阿基米德性質：不存在非零的無窮小。存在著數學上密切相關的有序代數結構是非阿基米德的，其中包括標準實數的各種各樣的替代品。0.999…的意義與這時使用的結構有關。例如，在對偶數中，引進了一個新的無窮小單位ε，就像複數系統中的虛數單位i一樣，但是ε² = 0。這樣便得出了一個在自動微分中十分有用的結構。這時可以給予對偶數一個字典序，這樣ε的倍數就非阿基米德原素。^[47]但是，要注意到，作為實數的延伸，在對偶數中仍然有0.999… = 1。儘管ε在對偶數中存在，ε/2也存在，所以ε就不是「最小的正對偶數」。確實是這樣，在實數中，並不存在這類的數。

另外一種構造標準實數的替代品的方法，是使用拓撲斯理論和替代的邏輯，而不是集合論和經典的邏輯（一種特殊情況）。例如，在光滑無窮小分析中，就存在沒有倒數的無窮小。^[48]

非標準分析因包含了一個有無窮小（及它們的反元素）完整陣列的系統而眾所周知，它提供了一個不同的，也許是更加直觀的，對微積分的處理。^[49]A.H. Lightstone在1972年提供了一個非標準小數展開式的發展，其中每一個位於（0, 1）之內的擴展的實數，都有一個唯一的擴展的小數展開式：數列0.ddd…；…ddd…，由擴展的自然數作索引。在這種形式中，0.333…有兩種自然的展開式，都不與¹/₃相差無窮小：

0.333…；…000…不存在，而

0.333…；…333…正好等於¹/₃。^[50]

組合博弈論也提供了替代的實數，無窮的藍-紅Hackenbush就是一個相關的例子。1974年，埃爾溫·伯利坎普描述了一個Hackenbush字串與實數的二進制展開式之間的對應關係，由數據壓縮的想法所促動。例如，Hackenbush字串LRRLRLRL…的值是0.010101₂… = ¹/₃。然而，LRLLL…的值（對應著0.111…₂）則與1相差無窮小。兩個數的差是超實數¹/_ω，其中ω是第一個無窮序數；相關的博弈是LRRRR…或0.000…₂。^[51]

打破減法的慣例

另外一種也可以使以上證明不成立的方法，就是1 − 0.999…根本就不存在，因為減法並不一定就是可能的。具有加法運算但沒有減法運算的數學結構包括可交換半群、可交換么半群，以及半環。里奇曼考慮了兩種這類的系統，使得0.999…< 1。

首先，里奇曼把非負的「小數」定義為字面上的小數展開式。他定義了字典序和一種加法運算，注意到0.999… < 1僅僅因為在個位數0 < 1，但對於任何一個有限小數x，都有0.999… + x = 1 + x。所以「小數」的一個獨特之處，是等式兩邊不能同減一個數；另外一個獨特之處，就是沒有「小數」對應著¹⁄₃。把乘法也定義了以後，「小數」便形成了一個正的、全序的、可交換的半環。^[52]

在定義乘法的過程中，里奇曼還定義了另外一種系統，他稱之為「分割D」，它是小數的戴德金分割的集合。通常用這種定義便可以得出實數，但對於小數d他既允許分割（−∞， d ），又允許「主分割」（−∞， d ]。這樣做的結果，就是實數與「小數」「不舒服地住在一起」。這個系統中也有0.999… < 1。在分割D中不存在正的無窮小，但存在一種「負的無窮小」──0⁻，它沒有小數展開式。里奇曼得出結論，0.999… = 1 + 0⁻，而方程「0.999… + x = 1」則沒有解。^[53]

p進數

主條目：p進數

問到關於0.999…的時候，初學者常常相信應該有一個「最後的9」，也就是說，相信1 − 0.999…等於一個正數，可以寫為「0.000…1」。不管那有沒有意義，目標都是明確的：把1加在0.999…中的最後的9上，就會把所有的9變成0，並在個位數留下一個1。如果考慮到其它的原因，這種想法便不成立了，這是因為在0.999…中，並不存在「最後的9」。^[54]對於包含最後的9的無窮多個9，這時必須從別的地方去尋找。

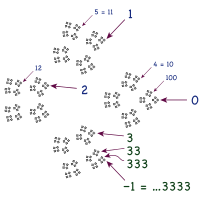
4進整數（黑點），包括數列（3，33，333，…）收斂於−1。10進數的類似等式，是…999 = −1。

p進數是在數論中引起興趣的又一個數系。像實數那樣，p進數可以從有理數通過柯西序列得到；但是，這種結構使用了另外一種度量，0與p之間的距離比0與1的距離還要近，而0與pⁿ的距離又比0與p的距離近。對於素數p來說，p進數便形成了一個域，而對於其它的p，包括10來說，則形成了一個環。所以在p進數中可以進行算術，這種數系也不存在無窮小。

在10進數中，類似於小數展開式的事物位於小數點的左面。10進展開式…999確實有一個最後的9，而沒有第一個9。這時可以把1加在個位數上，這樣進位之後就只剩下0了：1 + …999 = …000 = 0，所以…999 = −1。^[55]另外一種推導用到了等比級數。「…999」所指的無窮級數在實數中不收斂，但在10進數中收斂，所以這時可以使用大家熟悉的公式：

${\displaystyle \ldots 999=9+9(10)+9(10)^{2}+9(10)^{3}+\cdots ={\frac {9}{1-10}}=-1.}$^[56]

（與前面的級數比較。）第三種推導是一個七年級學生發明的，他對老師所講的0.999… = 1的極限證明感到懷疑，但因而產生了靈感，把以上乘以10的證明應用在相反的方向上：如果x = …999，則10x = …990，因此10x = x − 9，所以x = −1。^[55]

作為一個最後的延伸，由於0.999… = 1（在實數中），而…999 = −1（在10進數中），那麼這時可以「盲目、大膽地擺弄符號」，^[57]把兩個等式相加起來，得出：…999.999… = 0。這個等式在10進展開式中和標準小數展開式中都是沒有意義的，但假如這時研究出一種「雙小數」的理論，其中小數點左面和右面都可以無限延伸，那麼這個等式便是有意義和正確的。^[58]

相關問題

• 芝諾悖論，特別是奔跑者悖論，使人聯想起了0.999…等於1的表面上的悖論。奔跑者悖論可以建立一個數學模型，然後就可以像0.999…那樣，用等比級數的方法來解決。然而，這時不確定這種數學的論述是不是提到了芝諾所探索的形上學的問題。^[59]
• 除以零出現在0.999…的一些討論中，也引起了爭論。大部分作者都願意定義0.999…，但幾乎都不去定義除以零，這是因為它在實數系統中不可能有意義。然而，在某些其它的系統中，除以零則是有定義的，例如複數分析，其中擴展的複平面，也就是黎曼球面，在無窮遠處「有一個點」。在這裡，¹/₀便定義為無窮大；^[60]實際上，這個結果有深遠的意義，可以應用在工程和物理學中的許多問題上。有些著名的數學家在兩個系統發展起來之前就提出了這樣的一個定義。^[61]
• -0是另外一個記數的多餘特徵。在諸如實數的數系中，「0」表示加法單位元，既不是正數又不是負數，「−0」的解釋是0的相反數，這便迫使了−0 = 0。^[62]然而，在某些科學的應用中，使用了獨立的正零和負零，大多數常見的計算機記數系統就是這樣的（例如儲存在符號和大小或一補數的格式中的整數，或由IEEE二進制浮點數算術標準所指定的浮點數）。^[63][64]

參見

• 數學
• 算術
• 無窮（無限）
• 極限
• 小數表示法
• 非正式數學
• 非整數進位制
• 非標準分析
• 實分析
• 無窮級數

註解與引用

1. 華東師範大學. 数学分析. 高等教育出版社. : 3. ISBN 9787040506945.
2. 參見Silvanus P. Thompson的Calculus made easy中的二進制形式的證明，St. Martin's Press, New York, 1998. ISBN 978-0-312-18548-0.
3. Rudin p.61, Theorem 3.26; J. Stewart p.706
4. Euler p.170
5. Grattan-Guinness p.69; Bonnycastle p.177
6. 例如，J. Stewart p.706, Rudin p.61, Protter and Morrey p.213, Pugh p.180, J.B. Conway p.31
7. 這個極限可以由Rudin p. 57的Theorem 3.20e得出。對於一個更加直接的方法，請參見Finney, Weir, Giordano（2001）Thomas' Calculus: Early Transcendentals 10ed, Addison-Wesley, New York. Section 8.1, example 2 (a) , example 6(b).
8. Davies p.175; Smith and Harrington p.115
9. Beals p.22; I. Stewart p.34
10. Bartle and Sherbert pp.60–62; Pedrick p.29; Sohrab p.46
11. Apostol pp.9, 11–12; Beals p.22; Rosenlicht p.27
12. Apostol p.12
13. 歷史綜合首先由Griffiths and Hilton（p.xiv）在1970年聲稱，在2001年由Pugh（p.10）再次聲稱；兩本書都把戴德金切割視為公理。關於戴德金切割的應用，請參見Pugh p.17或Rudin p.17。關於邏輯上的觀點，請參見Pugh p.10、Rudin p.ix，或Munkres p.30。
14. Enderton（p.113）形容了這個描述：「戴德金分割背後的想法，是每一個實數x都可以用一個有理數的無窮集合，也就是所有小於x的有理數來命名。我們把x定義為小於x的有理數集合。為了避免循環定義，我們需要刻劃通過這種方法得出的有理數集合的特徵…」（「The idea behind Dedekind cuts is that a real number x can be named by giving an infinite set of rationals, namely all the rationals less than x. We will in effect define x to be the set of rationals smaller than x. To avoid circularity in the definition, we must be able to characterize the sets of rationals obtainable in this way…」）
15. Rudin pp.17–20、Richman p.399，或Enderton p.119。為了精確，魯丁（Rudin）、里奇曼和分別把這個分割稱為1*、1⁻，和1_R；三者都把它等同於傳統的實數1。注意魯丁和安德頓把它稱為戴德金分割，而里奇曼則把它稱為「非主戴德金分割」。
16. Richman p.399
17. J J O'Connor and E F Robertson. History topic: The real numbers: Stevin to Hilbert. MacTutor History of Mathematics. 2005-10 [2006-08-30]. （原始內容存檔於2007-09-29）.
18. Mathematics Magazine:Guidelines for Authors. Mathematical Association of America. [2006-08-23]. （原始內容存檔於2012-02-19）.
19. Richman pp.398–399
20. Griffiths & Hilton §24.2 "Sequences" p.386
21. Griffiths & Hilton pp.388, 393
22. Griffiths & Hilton pp.395
23. Griffiths & Hilton pp.viii, 395
24. Petkovšek p.408
25. Protter and Morrey p.503; Bartle and Sherbert p.61
26. Komornik and Loreti p.636
27. Kempner p.611; Petkovšek p.409
28. Petkovšek pp.410–411
29. Leavitt 1984 p.301
30. Lewittes pp.1–3; Leavitt 1967 pp.669,673; Shrader-Frechette pp.96–98
31. Pugh p.97; Alligood, Sauer, and Yorke pp.150–152. Protter and Morrey（p.507）和Pedrick（p.29）把這個描述作為一個練習。
32. Maor（p.60）和Mankiewicz（p.151）考察了第一種方法；Mankiewicz把它歸功於康托爾，但原始文獻不明。Munkres（p.50）提到了第二種方法。
33. Rudin p.50, Pugh p.98
34. Bunch p.119; Tall and Schwarzenberger p.6.最後一個建議要歸因於Burrell（p.28）："Perhaps the most reassuring of all numbers is 1.…So it is particularly unsettling when someone tries to pass off 0.9~ as 1."（「也許最令人放心的數就是1。…所以當把0.999…等同於1時，便感到特別彆扭。」）
35. Tall and Schwarzenberger pp.6–7; Tall 2000 p.221
36. Tall and Schwarzenberger p.6; Tall 2000 p.221
37. 非標準分析基礎　李邦河著
38. Tall 2000 p.221
39. Tall 1976 pp.10–14
40. Pinto and Tall p.5, Edwards and Ward pp.416–417
41. Mazur pp.137–141
42. Dubinsky et al. 261–262
43. 由Richman（p.396）觀察到。Hans de Vreught. sci.math FAQ: Why is 0.9999… = 1?. 1994 [2006-06-29]. （原始內容存檔於2007-09-29）.
44. Cecil Adams（英語：Cecil Adams）. An infinite question: Why doesn't .999~ = 1?. The Straight Dope（英語：The Straight Dope）. Chicago Reader（英語：Chicago Reader）. 2003-07-11 [2006-09-06]. （原始內容存檔於2012-01-10）.
45. Blizzard Entertainment Announces .999~（Repeating）= 1. Press Release. Blizzard Entertainment. 2004-04-01 [2006-09-03]. （原始內容存檔於2009-11-04）.
46. Gowers p.60
47. Berz 439–442
48. John L. Bell. An Invitation to Smooth Infinitesimal Analysis (PDF). 2003 [2006-06-29]. （原始內容存檔 (PDF)於2006-06-29）.
49. 對於一個完整的非標準數的論述，請參見Robinson的Non-standard Analysis。
50. Lightstone pp.245–247。在展開式的標準部分中，他沒有研究重複的9的可能性。
51. Berlekamp, Conway, and Guy（pp.79–80, 307–311）討論了1和¹/₃，也簡略地提到了¹/_ω。對於0.111…₂的博弈可以直接從伯利坎普法則得出，在以下的網站有所討論：A. N. Walker. Hackenstrings and the 0.999…? 1 FAQ. 1999 [2006-06-29]. （原始內容存檔於2006-06-16）.
52. Richman pp.397–399
53. Richman pp.398–400. Rudin（p.23）把這個替代的結構作為第一章的最後一個練習。
54. Gardiner p.98; Gowers p.60
55. Fjelstad p.11
56. Fjelstad pp.14–15
57. DeSua p.901
58. DeSua pp.902–903
59. Wallace p.51, Maor p.17
60. 參見J.B. Conway對默比烏斯變換的論述，pp.47–57。
61. Maor p.54
62. Munkres p.34, Exercise 1 (c)
63. Kroemer, Herbert; Kittel, Charles. Thermal Physics 2e. W. H. Freeman. 1980: 462. ISBN 978-0-7167-1088-2.
64. Floating point types. MSDN C# Language Specification. [2006-08-29]. （原始內容存檔於2006-08-24）.

參考文獻

• Alligood, Sauer, and Yorke. 4.1 Cantor Sets. Chaos: An introduction to dynamical systems. Springer. 1996. ISBN 978-0-387-94677-1.
• Apostol, Tom M. Mathematical analysis 2e. Addison-Wesley. 1974. ISBN 978-0-201-00288-1.
• Bartle, R.G. and D.R. Sherbert. Introduction to real analysis. Wiley. 1982. ISBN 978-0-471-05944-8.
• Beals, Richard. Analysis. Cambridge UP. 2004. ISBN 978-0-521-60047-7.
• Berlekamp, E.R.; J.H. Conway; and R.K. Guy. Winning Ways for your Mathematical Plays. Academic Press. 1982. ISBN 978-0-12-091101-1.
• Berz, Martin. Automatic differentiation as nonarchimedean analysis. Computer Arithmetic and Enclosure Methods. Elsevier: 439–450. 1992 [2007-10-13]. （原始內容存檔於2007-10-12）.
• Bunch, Bryan H. Mathematical fallacies and paradoxes. Van Nostrand Reinhold. 1982. ISBN 978-0-442-24905-2.
• Burrell, Brian. Merriam-Webster's Guide to Everyday Math: A Home and Business Reference. Merriam-Webster. 1998. ISBN 978-0-87779-621-3.
• Conway, John B. Functions of one complex variable I 2e. Springer-Verlag. 1978 [1973]. ISBN 978-0-387-90328-6.
• Davies, Charles. The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications. A.S. Barnes. 1846 [2007-10-13]. （原始內容存檔於2012-02-25）.
• DeSua, Frank C. A system isomorphic to the reals. The American Mathematical Monthly. 1960-11, 67 (9): 900–903.
• Dubinsky, Ed, Kirk Weller, Michael McDonald, and Anne Brown. Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2. Educational Studies in Mathematics. 2005, 60: 253–266. ISSN 0013-1954. doi:10.1007/s10649-005-0473-0.
• Edwards, Barbara and Michael Ward. Surprises from mathematics education research: Student (mis) use of mathematical definitions (PDF). The American Mathematical Monthly. 2004-05, 111 (5): 411–425 [2007-10-13]. （原始內容存檔 (PDF)於2011-07-22）.
• Enderton, Herbert B. Elements of set theory. Elsevier. 1977. ISBN 978-0-12-238440-0.
• Euler, Leonhard. John Hewlett and Francis Horner, English translators. , 編. Elements of Algebra 3rd English. Orme Longman. 1822 [1770] [2007-10-13]. （原始內容存檔於2012-11-11）.
• Fjelstad, Paul. The repeating integer paradox. The College Mathematics Journal. 1995-01, 26 (1): 11–15. doi:10.2307/2687285.
• Gardiner, Anthony. Understanding Infinity: The Mathematics of Infinite Processes. Dover. 2003 [1982]. ISBN 978-0-486-42538-2.
• Gowers, Timothy. Mathematics: A Very Short Introduction. Oxford UP. 2002. ISBN 978-0-19-285361-5.
• Grattan-Guinness, Ivor. The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. 1970. ISBN 978-0-262-07034-8.
• Griffiths, H.B.; Hilton, P.J. A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation. London: Van Nostrand Reinhold. 1970. ISBN 978-0-442-02863-3. LCC QA37.2 G75.
• Kempner, A.J. Anormal Systems of Numeration. The American Mathematical Monthly. 1936-12, 43 (10): 610–617.
• Komornik, Vilmos; and Paola Loreti. Unique Developments in Non-Integer Bases. The American Mathematical Monthly. 1998, 105 (7): 636–639.
• Leavitt, W.G. A Theorem on Repeating Decimals. The American Mathematical Monthly. 1967, 74 (6): 669–673.
• Leavitt, W.G. Repeating Decimals. The College Mathematics Journal. 1984-09, 15 (4): 299–308.
• Lewittes, Joseph. Midy's Theorem for Periodic Decimals. New York Number Theory Workshop on Combinatorial and Additive Number Theory. arXiv. 2006 [2007-10-13]. （原始內容存檔於2019-08-18）.
• Lightstone, A.H. Infinitesimals. The American Mathematical Monthly. 1972-03, 79 (3): 242–251.
• Mankiewicz, Richard. The story of mathematics. Cassell. 2000. ISBN 978-0-304-35473-3.
• Maor, Eli. To infinity and beyond: a cultural history of the infinite. Birkhäuser. 1987. ISBN 978-3-7643-3325-6.
• Mazur, Joseph. Euclid in the Rainforest: Discovering Universal Truths in Logic and Math. Pearson: Pi Press. 2005. ISBN 978-0-13-147994-4.
• Munkres, James R. Topology 2e. Prentice-Hall. 2000 [1975]. ISBN 978-0-13-181629-9.
• Pedrick, George. A First Course in Analysis. Springer. 1994. ISBN 978-0-387-94108-0.
• Petkovšek, Marko. Ambiguous Numbers are Dense. American Mathematical Monthly. 1990-05, 97 (5): 408–411.
• Pinto, Márcia and David Tall. Following students' development in a traditional university analysis course (PDF). PME25: v4: 57–64. 2001 [2007-10-13]. （原始內容存檔 (PDF)於2009-05-30）.
• Protter, M.H. and C.B. Morrey. A first course in real analysis 2e. Springer. 1991. ISBN 978-0-387-97437-8.
• Pugh, Charles Chapman. Real mathematical analysis. Springer-Verlag. 2001. ISBN 978-0-387-95297-0.
• Richman, Fred. Is 0.999… = 1?. Mathematics Magazine. 1999-12, 72 (5): 396–400.Free HTML preprint: Richman, Fred. Is 0.999… = 1?. 1999-06-08 [2006-08-23]. （原始內容存檔於2006-09-02）.
• Robinson, Abraham. Non-standard analysis Revised. Princeton University Press. 1996. ISBN 978-0-691-04490-3.
• Rosenlicht, Maxwell. Introduction to Analysis. Dover. 1985. ISBN 978-0-486-65038-8.
• Rudin, Walter. Principles of mathematical analysis 3e. McGraw-Hill. 1976 [1953]. ISBN 978-0-07-054235-8.
• Shrader-Frechette, Maurice. Complementary Rational Numbers. Mathematics Magazine. 1978-03, 51 (2): 90–98.
• Smith, Charles and Charles Harrington. Arithmetic for Schools. Macmillan. 1895 [2007-10-13]. （原始內容存檔於2012-02-25）.
• Sohrab, Houshang. Basic Real Analysis. Birkhäuser. 2003. ISBN 978-0-8176-4211-2.
• Stewart, Ian. The Foundations of Mathematics. Oxford UP. 1977. ISBN 978-0-19-853165-4.
• Stewart, James. Calculus: Early transcendentals 4e. Brooks/Cole. 1999. ISBN 978-0-534-36298-0.
• D.O. Tall and R.L.E. Schwarzenberger. Conflicts in the Learning of Real Numbers and Limits (PDF). Mathematics Teaching. 1978, 82: 44–49 [2007-10-13]. （原始內容存檔 (PDF)於2009-05-30）.
• Tall, David. Conflicts and Catastrophes in the Learning of Mathematics (PDF). Mathematical Education for Teaching. 1976-07, 2 (4): 2–18 [2007-10-13]. （原始內容存檔 (PDF)於2009-03-26）.
• Tall, David. Cognitive Development In Advanced Mathematics Using Technology (PDF). Mathematics Education Research Journal. 2000, 12 (3): 210–230 [2007-10-13]. （原始內容存檔 (PDF)於2009-05-30）.
• von Mangoldt, Dr. Hans. Reihenzahlen. Einführung in die höhere Mathematik 1st. Leipzig: Verlag von S. Hirzel. 1911.
• Wallace, David Foster. Everything and more: a compact history of infinity. Norton. 2003. ISBN 978-0-393-00338-3.

擴展閱讀

• Burkov, S. E. One-dimensional model of the quasicrystalline alloy. Journal of Statistical Physics. 1987, 47 (3/4): 409. doi:10.1007/BF01007518.
• Burn, Bob. 81.15 A Case of Conflict. The Mathematical Gazette. 1997-03, 81 (490): 109–112. JSTOR 3618786. doi:10.2307/3618786.
• Calvert, J. B.; Tuttle, E. R.; Martin, Michael S.; Warren, Peter. The Age of Newton: An Intensive Interdisciplinary Course. The History Teacher. 1981-02, 14 (2): 167–190. JSTOR 493261. doi:10.2307/493261.
• Choi, Younggi; Do, Jonghoon. Equality Involved in 0.999... and (-8)⅓. For the Learning of Mathematics. 2005-11, 25 (3): 13–15, 36. JSTOR 40248503.
• Choong, K. Y.; Daykin, D. E.; Rathbone, C. R. Rational Approximations to π. Mathematics of Computation. 1971-04, 25 (114): 387–392. JSTOR 2004936. doi:10.2307/2004936.
• Edwards, B. An undergraduate student's understanding and use of mathematical definitions in real analysis. Dossey, J., Swafford, J.O., Parmentier, M., Dossey, A.E. (編). Proceedings of the 19th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education 1. Columbus, OH: ERIC Clearinghouse for Science, Mathematics and Environmental Education. 1997: 17–22.
• Eisenmann, Petr. Why is it not true that 0.999... < 1? (PDF). The Teaching of Mathematics. 2008, 11 (1): 35–40 [2011-07-07]. （原始內容存檔 (PDF)於2011-08-15）.
• Ely, Robert. Nonstandard student conceptions about infinitesimals. Journal for Research in Mathematics Education. 2010, 41 (2): 117–146.

  This article is a field study involving a student who developed a Leibnizian-style theory of infinitesimals to help her understand calculus, and in particular to account for 0.999... falling short of 1 by an infinitesimal 0.000...1.

• Ferrini-Mundy, J.; Graham, K. Kaput, J.; Dubinsky, E. , 編. Research issues in undergraduate mathematics learning 33: 31–45. 1994.
• Lewittes, Joseph. Midy's Theorem for Periodic Decimals. 2006. arXiv:math.NT/0605182 .
• Katz, Karin Usadi; Katz, Mikhail G. Zooming in on infinitesimal 1 − .9.. in a post-triumvirate era. Educational Studies in Mathematics. 2010, 74 (3): 259. arXiv:1003.1501 . doi:10.1007/s10649-010-9239-4.
• Gardiner, Tony. Infinite processes in elementary mathematics: How much should we tell the children?. The Mathematical Gazette. 1985-06, 69 (448): 77–87. JSTOR 3616921. doi:10.2307/3616921.
• Monaghan, John. Real Mathematics: One Aspect of the Future of A-Level. The Mathematical Gazette. 1988-12, 72 (462): 276–281. JSTOR 3619940. doi:10.2307/3619940.
• Navarro, Maria Angeles; Carreras, Pedro Pérez. A Socratic methodological proposal for the study of the equality 0.999...=1 (PDF). The Teaching of Mathematics. 2010, 13 (1): 17–34 [2011-07-04]. （原始內容存檔 (PDF)於2011-08-15）.
• Przenioslo, Malgorzata. Images of the limit of function formed in the course of mathematical studies at the university. Educational Studies in Mathematics. 2004-03, 55 (1–3): 103–132. doi:10.1023/B:EDUC.0000017667.70982.05.
• Sandefur, James T. Using Self-Similarity to Find Length, Area, and Dimension. The American Mathematical Monthly. 1996-02, 103 (2): 107–120. JSTOR 2975103. doi:10.2307/2975103.
• Sierpińska, Anna. Humanities students and epistemological obstacles related to limits. Educational Studies in Mathematics. 1987-11, 18 (4): 371–396. JSTOR 3482354. doi:10.1007/BF00240986.
• Szydlik, Jennifer Earles. Mathematical Beliefs and Conceptual Understanding of the Limit of a Function. Journal for Research in Mathematics Education. 2000-05, 31 (3): 258–276. JSTOR 749807. doi:10.2307/749807.
• Tall, David O. Dynamic mathematics and the blending of knowledge structures in the calculus. ZDM Mathematics Education. 2009, 41 (4): 481–492. doi:10.1007/s11858-009-0192-6.
• Tall, David O. Intuitions of infinity. Mathematics in School. 1981-05, 10 (3): 30–33. JSTOR 30214290.

外部連結

• 數學主題

• When is .999... less than 1? Karin Usadi Katz and Mikhail G. Katz
• 0.999999… = 1?（頁面存檔備份，存於網際網路檔案館）來自cut-the-knot
• 為什麼0.9999... = 1？（頁面存檔備份，存於網際網路檔案館）
• 問一位科學家：重複的小數
• 基於算術的等式證明（頁面存檔備份，存於網際網路檔案館）
• 重複的九（頁面存檔備份，存於網際網路檔案館）
• 0.9循環等於1（頁面存檔備份，存於網際網路檔案館）
• 大衛·塔爾的研究（頁面存檔備份，存於網際網路檔案館）
• Metamath上的0.999...定理（頁面存檔備份，存於網際網路檔案館）
• 果殼網上的最讓人糾結的等式：0.999...=1（頁面存檔備份，存於網際網路檔案館）