雙曲函數

在數學中，雙曲函數是一類與常見的三角函數（也叫圓函數）類似的函數。最基本的雙曲函數是雙曲正弦函數${\displaystyle \sinh }$和雙曲餘弦函數${\displaystyle \cosh }$，從它們可以導出雙曲正切函數${\displaystyle \tanh }$等，其推導也類似於三角函數的推導。雙曲函數的反函數稱為反雙曲函數。

射線出原點交單位雙曲線${\displaystyle x^{2}-y^{2}=1}$於點${\displaystyle (\cosh a,\sinh a)}$，這裏的${\displaystyle a}$是射線、雙曲線和x軸圍成的面積的二倍。對於雙曲線上位於x軸下方的點，這個面積被認為是負值

雙曲函數示意圖

幾個雙曲函數的圖形。

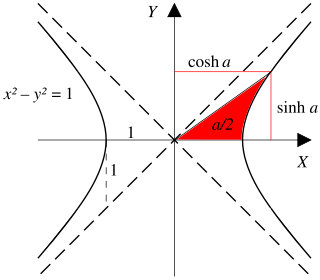
雙曲函數的定義域是實數，其自變量的值叫做雙曲角。雙曲函數出現於某些重要的線性微分方程的解中，譬如說定義懸鏈線和拉普拉斯方程。

基本定義

sinh、cosh和tanh

csch、sech和coth

最簡單的幾種雙曲函數為^[1]：

• 雙曲正弦：

  ${\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}}$

• 雙曲餘弦：

  ${\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}}$

• 雙曲正切：

  ${\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}.}$

• 雙曲餘切：當${\displaystyle x\neq 0}$

  ${\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}.}$

• 雙曲正割：

  ${\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}.}$

• 雙曲餘割：當${\displaystyle x\neq 0}$

  ${\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}.}$

函數${\displaystyle \cosh x}$是關於y軸對稱的偶函數。函數${\displaystyle \sinh x}$是奇函數。

如同當${\displaystyle t}$遍歷實數集${\displaystyle \mathbb {R} }$時，點（${\displaystyle \cos t}$, ${\displaystyle \sin t}$）的軌跡是一個圓${\displaystyle x^{2}+y^{2}=1}$一樣，當${\displaystyle t}$遍歷實數集${\displaystyle \mathbb {R} }$時，點（${\displaystyle \cosh t}$, ${\displaystyle \sinh t}$）的軌跡是單位雙曲線${\displaystyle x^{2}-y^{2}=1}$的右半邊。這是因為有以下的恆等式：

${\displaystyle \cosh ^{2}t-\sinh ^{2}t=1}$

參數t不是圓角而是雙曲角，它表示在x軸和連接原點和雙曲線上的點（${\displaystyle \cosh t}$, ${\displaystyle \sinh t}$）的直線之間的面積的兩倍。

歷史

在直角雙曲線（方程${\displaystyle y={1 \over x}}$）下，雙曲線三角形（黃色），和對應於雙曲角u的雙曲線扇形（紅色）。這個三角形的邊分別是雙曲函數中${\displaystyle \cosh }$和${\displaystyle \sinh }$的${\displaystyle {\sqrt {2}}}$倍。

在18世紀，約翰·海因里希·蘭伯特引入雙曲函數^[2]，並計算了雙曲幾何中雙曲三角形的面積^[3]。自然對數函數是在直角雙曲線${\displaystyle xy=1}$下定義的，可構造雙曲線直角三角形，底邊在線${\displaystyle y=x}$上，一個頂點是原點，另一個頂點在雙曲線。這裏以自然對數即雙曲角作為參數的函數，是自然對數的逆函數指數函數，即要形成指定雙曲角${\displaystyle u}$，在漸近線即x或y軸上需要有的${\displaystyle x}$或${\displaystyle y}$的值。顯見這裏的底邊是${\displaystyle \left(e^{u}+e^{-u}\right){\frac {\sqrt {2}}{2}}}$，垂線是${\displaystyle \left(e^{u}-e^{-u}\right){\frac {\sqrt {2}}{2}}}$。

通過旋轉和縮小線性變換，得到單位雙曲線下的情況，有：

• ${\displaystyle \cosh u={\frac {e^{u}+e^{-u}}{2}}}$
• ${\displaystyle \sinh u={\frac {e^{u}-e^{-u}}{2}}}$

單位雙曲線中雙曲線扇形的面積是對應直角雙曲線${\displaystyle xy=1}$下雙曲角的${\displaystyle {1 \over 2}}$。

虛數圓角定義

雙曲角經常定義得如同虛數圓角。實際上，如果${\displaystyle x}$是實數而${\displaystyle i^{2}=-1}$，則

${\displaystyle \cos(ix)=\cosh(x),\quad }$ ${\displaystyle -i\sin(ix)=\sinh(x).}$

所以雙曲函數${\displaystyle \cosh }$和${\displaystyle \sinh }$可以通過圓函數來定義。這些恆等式不是從圓或旋轉得來的，它們應當以無窮級數的方式來理解。特別是，可以將指數函數表達為由偶次項和奇次項組成，前者形成${\displaystyle \cosh }$函數，後者形成了${\displaystyle \sinh }$函數。${\displaystyle \cos }$函數的無窮級數可從${\displaystyle \cosh }$得出，通過把它變為交錯級數，而${\displaystyle \sin }$函數可來自將${\displaystyle \sinh }$變為交錯級數。上面的恆等式使用虛數${\displaystyle i}$，從三角函數的級數的項中去掉交錯因子${\displaystyle (-1)^{n}}$，來恢復為指數函數的那兩部份級數。

${\displaystyle e^{x}=\cosh x+\sinh x\!}$

${\displaystyle {\begin{array}{lcl}\cosh x=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&\sinh x=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}\\\cos x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}&\sin x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}\\\end{array}}}$

雙曲函數可以通過虛數圓角定義為：

• 雙曲正弦：^[1]

  ${\displaystyle \sinh x=-i\sin(ix)\!}$

• 雙曲餘弦：^[1]

  ${\displaystyle \cosh x=\cos(ix)\!}$

• 雙曲正切：

  ${\displaystyle \tanh x=-i\tan(ix)\!}$

• 雙曲餘切：

  ${\displaystyle \coth x=i\cot(ix)\!}$

• 雙曲正割：

  ${\displaystyle \operatorname {sech} x=\sec(ix)\!}$

• 雙曲餘割：

  ${\displaystyle \operatorname {csch} x=i\csc(ix)\!}$

這些複數形式的定義得出自歐拉公式。

與三角函數的類比

奧古斯都·德·摩根在其1849年出版的教科書《Trigonometry and Double Algebra》中將圓三角學擴展到了雙曲線^[4]。威廉·金頓·克利福德在1878年使用雙曲角來參數化單位雙曲線。

給定相同的角α，在雙曲線上計算雙曲角的量值（雙曲扇形面積除以半徑）得到雙曲函數，角${\displaystyle \alpha }$得到三角函數。在單位圓和單位雙曲線上，雙曲函數與三角函數有如下的關係:

• 正弦同樣是從x軸到曲線的半弦。
• 餘弦同樣是從y軸到曲線的半弦（圖中的餘弦是長方形的另一條邊）。
• 正切同樣是過x軸上單位點（1,0）在曲線上的切線到終邊的長度。
• 餘切同樣是從y軸與過終邊和曲線交點的切線與y軸的交點和曲線連線之長度。
• 正割同樣是在一個有正切和單位長的直角三角形上，但邊不一樣。
• 餘割同樣是y軸與過終邊和曲線交點的切線與y軸的交點和原點之距離。
• 角的量值可以從0到無限大，但${\displaystyle \alpha }$實際上只會介於${\displaystyle 0}$到${\displaystyle 2\pi }$（360度）之間，其餘是${\displaystyle \alpha }$的同界角，再繞着圓旋轉，故三角函數可以有周期。雙曲角的量值可以從${\displaystyle 0}$到無限大，但${\displaystyle \alpha }$實際上不會超過${\displaystyle {\frac {\pi }{4}}}$（45度），故無法如三角函數一樣有周期性。

恆等式

主條目：雙曲函數恆等式

與雙曲函數有關的恆等式如下:

${\displaystyle {\begin{aligned}\cosh ^{2}x-\sinh ^{2}x=1\\1-\tanh ^{2}x=\operatorname {sech} ^{2}x\\\operatorname {coth} ^{2}x-1=\operatorname {csch} ^{2}x\\\end{aligned}}}$

• 加法公式：

${\displaystyle \sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y}$

${\displaystyle \cosh(x+y)=\cosh x\cosh y+\sinh x\sinh y}$

${\displaystyle \tanh(x+y)={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}}$

• 二倍角公式：

${\displaystyle \sinh 2x\ =2\sinh x\cosh x}$

${\displaystyle \cosh 2x\ =\cosh ^{2}x+\sinh ^{2}x=2\cosh ^{2}x-1=2\sinh ^{2}x+1}$

${\displaystyle \tanh 2x={\frac {2\tanh x}{1+\tanh ^{2}x}}}$

• 和差化積：

${\displaystyle {\begin{aligned}\sinh x+\sinh y&=2\sinh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\cosh x+\cosh y&=2\cosh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\end{aligned}}}$

• 半角公式：

${\displaystyle \sinh {\frac {x}{2}}={\frac {\sinh x}{\sqrt {2(\cosh x+1)}}}=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}}$

${\displaystyle \cosh {\frac {x}{2}}={\sqrt {\frac {\cosh x+1}{2}}}}$

${\displaystyle \tanh {\frac {x}{2}}={\frac {\sinh x}{\cosh x+1}}=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}}$

其中 sgn 為符號函數。

若 x ≠ 0，則：

${\displaystyle \tanh {\frac {x}{2}}={\frac {\cosh x-1}{\sinh x}}=\coth x-\operatorname {csch} x}$

由於雙曲函數和三角函數之間的對應關係，雙曲函數的恆等式和三角函數的恆等式之間也是一一對應的。對於一個已知的三角函數公式，只需要將其中的三角函數轉成相應的雙曲函數，並將含有有兩個${\displaystyle \sinh }$的積的項（包括${\displaystyle \coth ^{2}x,\tanh ^{2}x,\operatorname {csch} ^{2}x,\sinh x\sinh y}$）轉換正負號，就可得到相應的雙曲函數恆等式^[5]。如

• 三倍角公式：

三角函數的三倍角公式為：

${\displaystyle \sin 3x\ =3\sin x-4\sin ^{3}x}$

${\displaystyle \cos 3x\ =-3\cos x+4\cos ^{3}x}$

而對應的雙曲函數三倍角公式則是：

${\displaystyle \sinh 3x\ =3\sinh x+4\sinh ^{3}x}$

${\displaystyle \cosh 3x\ =-3\cosh x+4\cosh ^{3}x}$

• 差角公式：

${\displaystyle {\begin{aligned}\sinh(x-y)&=\sinh x\cosh y-\cosh x\sinh y\\\cosh(x-y)&=\cosh x\cosh y-\sinh x\sinh y\\\tanh(x-y)&={\frac {\tanh x-\tanh y}{1-\tanh x\tanh y}}\\\end{aligned}}}$

雙曲函數的導數

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\sinh x&=\cosh x\\{\frac {d}{dx}}\cosh x&=\sinh x\\{\frac {d}{dx}}\tanh x&=1-\tanh ^{2}x=\operatorname {sech} ^{2}x={\frac {1}{\cosh ^{2}x}}\\{\frac {d}{dx}}\coth x&=1-\coth ^{2}x=-\operatorname {csch} ^{2}x=-{\frac {1}{\sinh ^{2}x}}&&x\neq 0\\{\frac {d}{dx}}\operatorname {sech} x&=-\tanh x\operatorname {sech} x\\{\frac {d}{dx}}\operatorname {csch} x&=-\coth x\operatorname {csch} x&&x\neq 0\end{aligned}}}$

雙曲函數的泰勒展開式

雙曲函數也可以以泰勒級數展開:

${\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}$

${\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}$

${\displaystyle \tanh x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}$

${\displaystyle \coth x={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }$（羅朗級數）

${\displaystyle \operatorname {sech} \,x=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}$

${\displaystyle \operatorname {csch} \,x={\frac {1}{x}}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }$（羅朗級數）

其中

${\displaystyle B_{n}}$是第${\displaystyle n}$項伯努利數

${\displaystyle E_{n}}$是第${\displaystyle n}$項歐拉數

無限積與連續分數形式

下列的擴展在整個複數平面上成立：

${\displaystyle \sinh x=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{n^{2}\pi ^{2}}}\right)={\cfrac {x}{1-{\cfrac {x^{2}}{2\cdot 3+x^{2}-{\cfrac {2\cdot 3x^{2}}{4\cdot 5+x^{2}-{\cfrac {4\cdot 5x^{2}}{6\cdot 7+x^{2}-\ddots }}}}}}}}}$

${\displaystyle \cosh x=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{(n-1/2)^{2}\pi ^{2}}}\right)={\cfrac {1}{1-{\cfrac {x^{2}}{1\cdot 2+x^{2}-{\cfrac {1\cdot 2x^{2}}{3\cdot 4+x^{2}-{\cfrac {3\cdot 4x^{2}}{5\cdot 6+x^{2}-\ddots }}}}}}}}}$

${\displaystyle \tanh x={\cfrac {1}{{\cfrac {1}{x}}+{\cfrac {1}{{\cfrac {3}{x}}+{\cfrac {1}{{\cfrac {5}{x}}+{\cfrac {1}{{\cfrac {7}{x}}+\ddots }}}}}}}}}$

雙曲函數的積分

${\displaystyle \int \sinh cx\,\mathrm {d} x={\frac {1}{c}}\cosh cx+C}$

${\displaystyle \int \cosh cx\,\mathrm {d} x={\frac {1}{c}}\sinh cx+C}$

${\displaystyle \int \tanh cx\,\mathrm {d} x={\frac {1}{c}}\ln(\cosh cx)+C}$

${\displaystyle \int \coth cx\,\mathrm {d} x={\frac {1}{c}}\ln \left|\sinh cx\right|+C}$

${\displaystyle \int \operatorname {sech} cx\,\mathrm {d} x={\frac {1}{c}}\arctan(\sinh cx)+C}$

${\displaystyle \int \operatorname {csch} cx\,\mathrm {d} x={\frac {1}{c}}\ln \left|\tanh {\frac {cx}{2}}\right|+C}$

與指數函數的關係

從雙曲正弦和餘弦的定義，可以得出如下恆等式:

${\displaystyle e^{x}=\cosh x+\sinh x}$

和

${\displaystyle e^{-x}=\cosh x-\sinh x}$

複數的雙曲函數

因為指數函數可以定義為任何複數參數，也可以擴展雙曲函數的定義為複數參數。函數${\displaystyle \sinh z}$和${\displaystyle \cosh z}$是全純函數。

指數函數與三角函數的關係由歐拉公式給出：

${\displaystyle {\begin{aligned}e^{ix}&=\cos x+i\;\sin x\\e^{-ix}&=\cos x-i\;\sin x\end{aligned}}}$

所以:

${\displaystyle {\begin{aligned}\cosh ix&={\frac {1}{2}}\left(e^{ix}+e^{-ix}\right)=\cos x\\\sinh ix&={\frac {1}{2}}\left(e^{ix}-e^{-ix}\right)=i\sin x\\\tanh ix&=i\tan x\\\end{aligned}}}$

${\displaystyle {\begin{aligned}\cosh(x+iy)&=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\\\sinh(x+iy)&=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\\\end{aligned}}}$

${\displaystyle {\begin{aligned}\cosh x&=\cos ix\\\sinh x&=-i\sin ix\\\tanh x&=-i\tan ix\end{aligned}}}$

因此，雙曲函數是關於虛部有週期的，週期為${\displaystyle 2\pi i}$（對雙曲正切和餘切是${\displaystyle \pi i}$）。

反雙曲函數

主條目：反雙曲函數

反雙曲函數是雙曲函數的反函數。它們的定義為：

${\displaystyle {\begin{aligned}\operatorname {arsinh} (x)&=\ln \left(x+{\sqrt {x^{2}+1}}\right)\\\operatorname {arcosh} (x)&=\ln \left(x+{\sqrt {x^{2}-1}}\right);x\geq 1\\\operatorname {artanh} (x)&={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right);\left|x\right|<1\\\operatorname {arcoth} (x)&={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right);\left|x\right|>1\\\operatorname {arsech} (x)&=\ln \left({\frac {1}{x}}+{\frac {\sqrt {1-x^{2}}}{x}}\right);0<x\leq 1\\\operatorname {arcsch} (x)&=\ln \left({\frac {1}{x}}+{\frac {\sqrt {1+x^{2}}}{\left|x\right|}}\right);x\neq 0\end{aligned}}}$

參考文獻

1. Weisstein, Eric W. (編). Hyperbolic Functions. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2020-08-29]. （原始內容存檔於2022-05-21） （英語）.
2. Eves, Howard, Foundations and Fundamental Concepts of Mathematics, Courier Dover Publications: 59, 2012, ISBN 9780486132204, We also owe to Lambert the first systematic development of the theory of hyperbolic functions and, indeed, our present notation for these functions.
3. Ratcliffe, John, Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics 149, Springer: 99, 2006 [2014-03-27], ISBN 9780387331973, （原始內容存檔於2014-01-12）, That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786.
4. Augustus De Morgan (1849) Trigonometry and Double Algebra （頁面存檔備份，存於互聯網檔案館）, Chapter VI: "On the connection of common and hyperbolic trigonometry"
5. G. Osborn, Mnemonic for hyperbolic formulae^{[失效連結]}, The Mathematical Gazette, p. 189, volume 2, issue 34, July 1902

參見

• 反雙曲函數
• 雙曲函數符號
• 三角函數
• 古德曼函數