Loading AI tools
来自维基百科,自由的百科全书
在泛函分析中,捲積(convolution),或譯為疊積、褶積或旋積,是透過兩個函數和生成第三個函數的一種數學算子,表徵函數與經過翻轉和平移的的乘積函數所圍成的曲邊梯形的面積。如果將參加卷積的一個函數看作區間的指示函數,卷積還可以被看作是「滑動平均」的推廣。

卷積是數學分析中一種重要的運算。設:和是實數上的兩個可積函數,定義二者的卷積為如下特定形式的積分轉換:
仍為可積函數,並且有着:
函數和,如果只支撐在之上,則積分界限可以截斷為:
對於兩個得出複數值的多元實變函數,可以定義二者的卷積為如下形式的多重積分:
卷積有一個通用的工程上的符號約定[1]:
它必須被謹慎解釋以避免混淆。例如:等價於,而卻實際上等價於[2]。
卷積運算的最早使用出現在達朗貝爾於1754年出版的《宇宙體系的幾個要點研究》中對泰勒定理的推導之中[3]。還有西爾維斯特·拉克魯瓦,將類型的表達式,用在他的1797年–1800年出版的著作《微分與級數論文》中[4]。此後不久,卷積運算出現在皮埃爾-西蒙·拉普拉斯、約瑟夫·傅立葉和西梅翁·泊松等人的著作中。這個運算以前有時叫做「Faltung」(德語中的摺疊)、合成乘積、疊加積分或卡森積分[5]。
「卷積」這個術語早在1903年就出現了,然而其定義在早期使用中是相當生僻的[6][7],直到1950年代或1960年代之前都未曾廣泛使用。
如果和都是在Lp 空間內的勒貝格可積函數,則二者的卷積存在,並且在這種情況下也是可積的[8]。這是托內利定理的結論。對於在中的函數在離散卷積下,或更一般的對於在任何群的上的卷積,這也是成立的。同樣的,如果而,這裏的,則,並且其Lp 範數間有着不等式:
在的特殊情況下,這顯示出是在卷積下的巴拿赫代數(並且如果和幾乎處處非負則兩邊間等式成立)。
卷積與傅立葉轉換有着密切的關係。例如兩函數的傅立葉轉換的乘積等於它們卷積後的傅立葉轉換,利用此一性質,能簡化傅立葉分析中的許多問題。
由卷積得到的函數,一般要比和都光滑。特別當為具有緊支集的光滑函數,為局部可積時,它們的卷積也是光滑函數。利用這一性質,對於任意的可積函數,都可以簡單地構造出一列逼近於的光滑函數列,這種方法稱為函數的光滑化或正則化。
這裏的叫做移位(displacement)或滯後(lag)。
對於單位脈衝函數和某個函數,二者得到的捲積就是本身,此被稱為衝激響應:
在連續時間線性非時變系統中,輸出訊號被描述為輸入訊號與脈衝響應的卷積[9]:
兩個獨立的隨機變量和,每個都有一個概率密度函數,二者之和的概率密度,是它們單獨的密度函數的卷積:
|

|
| 兩個矩形脈衝波的捲積。其中函數首先對反射,接着平移,成為。那麼重疊部份的面積就相當於處的卷積,其中橫坐標代表待變量以及新函數的自變量。 | 
|
| 矩形脈衝波和指數衰減脈衝波的捲積(後者可能出現於RC電路中),同樣地重疊部份面積就相當於處的捲積。注意到因為是對稱的,所以在這兩張圖中,反射並不會改變它的形狀。 | 
|
這裏的是任意參數。
任何可積分函數,都可以通過求函數的所有整數倍的平移的總和,從而製作出具有週期的週期函數 ,這叫做週期求和:
對於無週期函數與,其週期的週期求和分別是與,與的週期卷積,可以定義為與的常規卷積,或與的常規卷積,二者都等價於與的週期積分:
圓周卷積是週期卷積的特殊情況[11][12],其中函數和二者的非零部份,都限定在區間之內,此時的週期求和稱為「週期延拓」。中函數可以通過取非負餘數的模除運算表達為「圓周函數」:
而積分的界限可以縮簡至函數的長度範圍:

對於定義在整數上且得出複數值的函數和,離散卷積定義為[13]:
這裏一樣把函數定義域以外的值當成零,所以可以擴展函數到所有整數上(如果本來不是的話)。兩個有限序列的卷積的定義,是將這些序列擴展成在整數集合上有限支撐的函數。在這些序列是兩個多項式的系數之時,這兩個多項式的普通乘積的系數,就是這兩個序列的卷積。這叫做序列系數的柯西乘積。
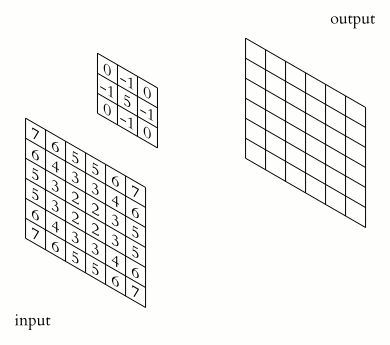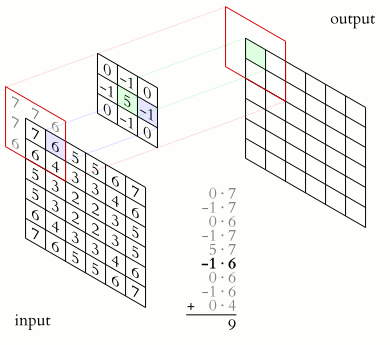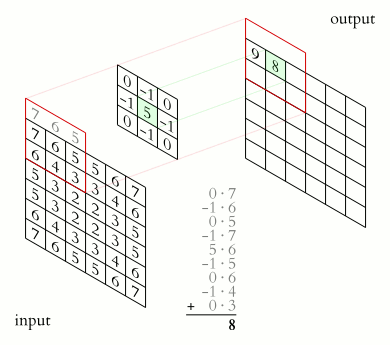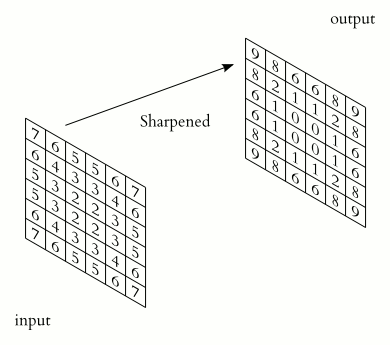
類似於一維情況,使用星號表示卷積,而維度體現在星號的數量上,維卷積就寫為個星號。下面是維訊號的卷積的表示法:
對於離散值的訊號,這個卷積可以直接如下這樣計算:
結果的離散多維卷積所支撐的輸出區域,基於兩個輸入訊號所支撐的大小和區域來決定。

對於離散序列和一個參數,無週期函數和的「週期卷積」是為:
這個函數有週期,它有最多個唯一性的值。和的非零範圍都是的特殊情況叫做圓周卷積:
離散圓周卷積可簡約為矩陣乘法,這裏的積分轉換的核函數是循環矩陣:
各種卷積算子都滿足下列性質:
如果和是可積分函數,則它們在整個空間上的卷積的積分,簡單的就是它們積分的乘積[14]:
在一元函數情況下,和的卷積的導數有着:
這裏的是微分算子。更一般的說,在多元函數的情況下,對偏導數也有類似的公式:
這就有了一個特殊結論,卷積可以看作「光滑」運算:和的卷積可微分的次數,是和的總數。
這些恆等式成立的嚴格條件,為和是絕對可積分的,並且至少二者之一有絕對可積分()弱導數,這是Young卷積不等式的結論。
卷積定理指出[15],在適當的條件下,兩個函數(或訊號)的卷積的傅立葉轉換,是它們的傅立葉轉換的逐點乘積。更一般的說,在一個域(比如時域)中的卷積等於在其他域(比如頻域)逐點乘法。
設兩個函數和,分別具有傅立葉轉換和:
卷積定理聲稱:
應用逆傅立葉轉換產生推論:
這裏的算符指示逐點乘法。
這一定理對拉普拉斯轉換、雙邊拉普拉斯轉換、Z轉換、梅林轉換和Hartley轉換等各種傅立葉轉換的變體同樣成立。在調和分析中還可以推廣到在局部緊緻的阿貝爾群上定義的傅立葉轉換。
對於週期為的函數和,可以被表達為二者的週期求和:
逐點乘積的週期也是,它的傅立葉級數系數為:
週期卷積的週期也是,週期卷積的卷積定理為:
對於作為兩個連續函數取樣的序列和,它們具有離散時間傅立葉轉換和:
這裏的算子指示離散時間傅立葉轉換(DTFT)。
離散卷積的卷積定理為:
對於週期為的序列和:
相較於離散時間傅立葉轉換和的週期是,它們是按間隔取樣和,並在個取樣上進行了逆離散傅立葉轉換(DFT-1或IDFT)的結果。
離散週期卷積的週期也是。離散週期卷積定理為:
這裏的算子指示長度的離散傅立葉轉換(DFT)。
它有着推論:
對於其非零時段小於等於的和,離散圓周卷積的卷積定理為:
卷積的概念還可以推廣到數列、測度以及廣義函數上去。函數是定義在上的可測函數(measurable function),與存在卷積並記作。如果函數不是定義在上,可以把函數定義域以外的值都規定成零,這樣就變成一個定義在上的函數。
若G是有某m 測度的群(例如郝斯多夫空間上哈爾測度下局部緊緻的拓撲群),對於G上m-勒貝格可積的實數或複數函數f和g,可定義它們的卷積:
計算卷積有三種主要的方法,分別為
方法1是直接利用定義來計算卷積,而方法2和3都是用到了FFT來快速計算卷積。也有不需要用到FFT的作法,如使用數論轉換。
分段卷積: Overlap-Add
欲做的分段卷積分, 長度為 , 長度為 ,
Step 1: 將每 分成一段
Step 2: 再每段 點後面添加 個零,變成長度
Step 3: 把 添加 個零,變成長度 的
Step 4: 把每個 的小段和 做快速卷積,也就是,每小段會得到長度 的時域訊號
Step 5: 放置第 個小段的起點在位置 上,
Step 6: 會發現在每一段的後面 點有重疊,將所有點都相加起來,顧名思義 Overlap-Add,最後得到結果
舉例來說:
, 長度
, 長度
令
令 切成三段,分別為 , 每段填 個零,並將 填零至長度
將每一段做
若將每小段擺在一起,可以注意到第一段的範圍是 ,第二段的範圍是 ,第三段的範圍是 ,三段的範圍是有重疊的
最後將三小段加在一起,並將結果和未分段的卷積做比較,上圖是分段的結果,下圖是沒有分段並利用快速卷積所算出的結果,驗證兩者運算結果相同。
分段卷積: Overlap-Save
欲做的分段卷積分, 長度為 , 長度為 ,
Step 1: 將 前面填 個零
Step 2: 第一段 , 從新的 中 取到 總共 點當做一段,因此每小段會重複取到前一小段的 點,取到新的一段全為零為止
Step 3: 把 添加 個零,變成長度 的
Step 4: 把每個 的小段和 做快速卷積,也就是,每小段會得到長度 的時域訊號
Step 5: 對於每個 小段,只會保留末端的 點,因此得名 Overlap-Save
Step 6: 將所有保留的點合再一起,得到最後結果
舉例來說:
, 長度
, 長度
令
將 前面填 個零以後,按照 Step 2 的方式分段,可以看到每一段都重複上一段的 點
再將每一段做 以後可以得到
保留每一段末端的 點,擺在一起以後,可以注意到第一段的範圍是 ,第二段的範圍是 ,第三段的範圍是 ,第四段的範圍是 ,四段的範圍是沒有重疊的
將結果和未分段的卷積做比較,下圖是分段的結果,上圖是沒有分段並利用快速卷積所算出的結果,驗證兩者運算結果相同。
至於為什麼要把前面 丟掉?
以下以一例子來闡述:
, 長度 ,
, 長度 ,
第一條藍線代表 軸,而兩條藍線之間代表長度 ,是在做快速卷積時的週期
當在做快速卷積時,是把訊號視為週期 ,在時域上為循環卷積分,
而在一開始前 點所得到的值,是 和 內積的值,
然而 這 個值應該要為零,以往在做快速卷積時長度為 時不會遇到這些問題,
而今天因為在做快速卷積時長度為 才會把這 點算進來,因此我們要丟棄這 點內積的結果
為了要丟棄這 點內積的結果,位移 點,並把位移以後內積合的值才算有效。
以上三種方法皆可用來計算卷積,其差別在於所需總體乘法量不同。基於運算量以及效率的考量,在計算卷積時,通常會選擇所需總體乘法量較少的方法。
以下根據和的長度()分成5類,並列出適合使用的方法:
基本上,以上只是粗略的分類。在實際應用時,最好還是算出三種方法所需的總乘法量,再選擇其中最有效率的方法來計算卷積。
Q1:當,適合用哪種方法計算卷積?
Ans:
Q2:當,適合用哪種方法計算卷積?
Ans:
Q3:當,適合用哪種方法計算卷積?
Ans:

卷積在科學、工程和數學上都有很多應用:
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.