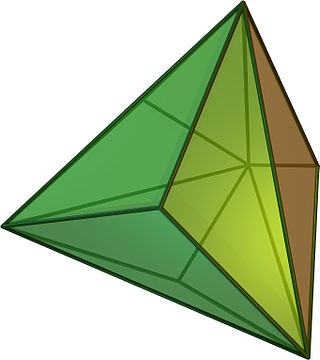
三角化四面體

在幾何學中，三角化四面體（英語：triakis tetrahedron或kistetrahedron^[2]）是一種卡塔蘭多面體，其為截角正四面體的對偶多面體^[3]。

三角化四面體

（點選檢視旋轉模型）
類別	卡塔蘭立體
對偶多面體	截角正四面體
識別
鮑爾斯縮寫 （verse-and-dimensions的wikia：Bowers acronym）	tikit
數學表示法
考克斯特符號 （英語：Coxeter-Dynkin diagram）
性質
面	12
邊	18
頂點	8
歐拉特徵數	F=12, E=18, V=8 （χ=2）
二面角	129° 31' 16" ${\displaystyle \arccos(-{\frac {7}{11}})}$
組成與佈局
面的種類	等腰三角形
面的佈局 （英語：Face configuration）	V3.6.6
頂點圖	4{3}+4{6}
對稱性
對稱群	Td, A3, [3,3], *332
旋轉對稱群 （英語：Rotation_groups）	T, [3,3]+, 332
特性
凸、face-transitive
圖像
截角正四面體 （對偶多面體） （展開圖）

在礦物學中，這種形狀又稱為三四面體^[4]（英語：tristetrahedron^[5][6]）。

性質

三角化四面體的旋轉透視圖。

三角化四面體是一種卡塔蘭立體，由12個面、18條邊和8個頂點組成^[7]，對偶多面體是一個阿基米德立體——截角四面體^[7][3]。由於其對偶多面體具有點可遞的性質，因此三角化四面體擁有面可遞的性質，即所有面皆全等。三角化四面體由12個全等的等腰三角形組成，其頂點有兩種：一種為3個等腰三角形的公共頂點，另一種為6個等腰三角形的公共頂點。

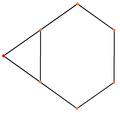
三角化四面體可以看做是在正四面體每個面上加上錐高為${\displaystyle {\frac {\sqrt {6}}{15}}}$倍邊長的三角錐後所形成的形狀^[8]，可以視為正三角形三邊各加一個等腰三角形拼成的正六邊形在立體幾何中的推廣。

面的組成

三角化四面體的面由12個全等的等腰三角形組成^[9]，三角形的邊長比為3:3:5^[10][9]。

組成三角化四面體的等腰三角形，其頂角為${\displaystyle 2\cot ^{-1}{\frac {\sqrt {11}}{5}}}$約為112.89°、底角為${\displaystyle \tan ^{-1}{\frac {\sqrt {11}}{5}}}$約為33.56°。

體積與表面積

一個最短邊長為單位長的三角化四面體，它的表面積為${\displaystyle {\tfrac {5}{3}}\scriptstyle {\sqrt {11}}}$，體積為${\displaystyle {\tfrac {25}{36}}\scriptstyle {\sqrt {2}}}$^[8]。

另一方面，也可以從其對偶多面體來計算體積。若其對偶多面體——截角四面體邊長為a，可以先得出三角化四面體的邊長：

短邊為${\displaystyle {\frac {9}{5}}a=1.8a}$個單位長^[10][8]

長邊為3a個單位長^[10][8]

半周長為${\displaystyle S={\frac {2\times {\frac {9}{5}}+3}{2}}a=3.3a}$，透過海倫公式可求得一個面的面積：

${\displaystyle {\sqrt {s(s-a)(s-b)(s-c)}}={\sqrt {3.3(3.3-{\frac {9}{5}})^{2}(3.3-3)}}a^{2}={\frac {9{\sqrt {11}}}{20}}a^{2}\approx 1.49248a^{2}}$^{[註 1]}

則體積V與表面積A為^[10]：

${\displaystyle V={\frac {81{\sqrt {2}}}{20}}a^{3}\approx 5.72756a^{3}}$

${\displaystyle A={\frac {27{\sqrt {11}}}{5}}a^{2}\approx 17.90977a^{2}}$

二面角

三角化四面體的二面角有2種結構，一種是等腰三角形長邊與長邊的二面角，另一種是短邊與短邊的二面角。兩個二面角角度皆相同，其值為負十一分之七的反餘弦值^[10]：

${\displaystyle \cos ^{-1}\left(-{\frac {7}{11}}\right)\approx 2.26057\approx 129.521196^{\circ }}$^[10]

正交投影

三角化四面體有4個特殊的正交投影，分別為於稜上投影（兩種）、於面上投影和於面與頂點上投影。

正交投影

投影位置	於稜上投影	於面上投影	於面與頂點上投影	於稜上投影（交叉）
三角化 四面體
（對偶） 截角 四面體
投影 對稱性	[1]	[1]	[3]	[4]

相關多面體與鑲嵌

球面鑲嵌版本的三角化四面體

三角化四面體是正四面體經過三角化變換後的結果，其他也是由正四面體透過康威變換得到的多面體有：

正四面體家族半正多面體

對稱性: [3,3], (*332)							[3,3]+, (332)
{3,3}	t0,1{3,3}	t1{3,3}	t1,2{3,3}	t2{3,3}	t0,2{3,3}	t0,1,2{3,3}	s{3,3}
半正多面體對偶
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

三角化四面體是由等腰三角形組成，且對偶多面體由正六邊形與正三角形交錯組成。同樣由等腰三角形組成，且對偶多面體由正多邊形與正三角形交錯組成的多面體或鑲嵌圖包括：

*n32變異對稱性的截角鑲嵌（英語：Template:Truncated figure1 table）: 3.2n.2n

對稱性 *n32 [n,3]	球面鑲嵌（英語：List_of_spherical_symmetry_groups）				歐氏鑲嵌（英語：List_of_planar_symmetry_groups）	緊湊雙曲		非緊雙曲
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
截角鑲嵌
頂點（英語：Vertex configuration）	3.4.4	3.6.6	3.8.8	3.10.10	3.12.12	3.14.14（英語：Truncated_heptagonal_tiling）	3.16.16（英語：Truncated octagonal tiling）	3.∞.∞（英語：Truncated order-3 apeirogonal tiling）
三角化 鑲嵌
頂點（英語：Vertex configuration）	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14（英語：Truncated_heptagonal_tiling#Dual_tiling）	V3.16.16（英語：Truncated_octagonal_tiling#Dual_tiling）	V3.∞.∞（英語：Truncated_order-3_apeirogonal_tiling#Dual_tiling）

對偶複合體

複合截角四面體三角化四面體

複合截角四面體三角化四面體
類別	複合半正多面體
對偶多面體	自身對偶
性質
體	2
面	20
邊	36
頂點	20
歐拉特徵數	F=20, E=36, V=20 （χ=4）
組成與佈局
複合幾何體數量	2
複合幾何體種類	1個三角化四面體 1個截角四面體
面的種類	12個等腰三角形 4個正三角形 4個正六邊形
對稱性
對稱群	四面體群 (Td)

對偶複合體，即一個多面體與其對偶多面體組合成的複合圖形。三角化四面體與其對偶的複合體為複合截角四面體三角化四面體。其共有20個面、36條邊和20個頂點，其尤拉示性數為4，虧格為-1^[11]。

正交投影

以正六邊形面為中心

以正三角形面為中心

面的組成

複合截角四面體三角化四面體由4個正三角形、4個正六邊形和12個等腰三角形組成，其中組成的等腰三角形與三角化四面體完全相同，邊長比同為3:3:5，但有部分隱沒在截角四面體中，如下圖所示，露在該立體外部的部分，以藍色表示，隱沒在立體內部的部分以白色表示，其中黑線代表等腰三角形與其對偶多面體截角四面體相交的位置：

複合截角四面體三角化四面體中的截角四面體亦有部分隱沒在三角化四面體中，如下圖所示：

正六邊形面

正三角形面

對偶多面體

主條目：截角四面體

三角化四面體

對偶多面體： 截角四面體

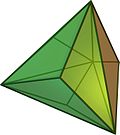
三角化四面體的對偶多面體是一種由4個正三角形和4個正六邊形組成的多面體^[12]，有12個頂點和18條棱，可以想象為將正四面體的頂點切去，稱為截角四面體^[7][3][8]。

四半面體對稱性

三角化四面體可以看做是四半面體^[13]對稱性退化的極限：

四半面體變體的範例

其他變體

三角化四面體為正四面體每個面都加上適當高度的角錐所形成的幾何形狀^[9]。

而若加入的角錐為正三角錐（正四面體）則會產生正五胞體的展開圖：

而若加入的角錐為直角三角錐，則會使等腰三角形兩兩共面形成立方體。可以透過在立方體的面上畫上六個對角線看出此特性：

參見

• 截角三角化四面體