热门问题
时间线
聊天
视角
除以零
將某數除以0的運算 来自维基百科,自由的百科全书
Remove ads
在数学中,被除数的除数(分母)是零或将某数除以零,可表达为,是被除数。在算式中没有意义,因为没有数目,以零相乘(假设),由于任何数字乘以零均等于零,因此除以零是一个没有定义的值。此式是否成立端视其在如何的数学设定下计算。一般实数算术中,此式为无意义。在程序设计中,当遇上正整数除以零程序会中止,正如浮点数会出现无限大或NaN值的情况,而在Microsoft Excel及Openoffice或Libreoffice的Calc中,除以零会直接显示#DIV/0! 。

Remove ads
基本算术
基本算术中,除法指将一个集合中的物件分成若干等份。例如,个苹果平分给人,每人可得个苹果。同理,个苹果只分给人,则其可独得个苹果。
若除以又如何?若有颗苹果,无人(解作没有)来分,每“人”可得多少苹果?问题本身是无意义的,因根本无人来,论每“人”可得多少,根本多馀。因此,,在基本算术中,是无意义或未下定义的。
另种解释是将除法理解为不断的减法。例如“除以”,换一种说法,减去两个,馀下,即被除数一直减去除数直至馀数数值低于除数,算式为馀数。若某数除以零,就算不断减去零,馀数也不可能小于除数,使得算式与无穷拉上关系,超出基本算术的范畴。此解释也有一问题,即为无穷大乘以零仍是零。
Remove ads
婆罗摩笈多(598–668年)的著作《婆罗摩历算书》被视为最早讨论零的数学和定义涉及零的算式的文本。但当中对除以零的论述并不正确,根据婆罗摩笈多所说,
| “ | 一个正或负整数除以零,成为以零为分母的分数。零除以正或负整数是零或以零为分子、该正或负整数为分母的分数。零除以零是零。 | ” |
830年,另一位数学家摩诃吠罗在其著作《计算精华》试图纠正婆罗摩笈多的错误,但不成功:
| “ | 一数字除以零会维持不变。 | ” |
婆什迦罗第二尝试解决此问题,答案是让。虽然此定义有一定道理,但会导致一个悖论:的结果可以是任意一个数,所以所有的数都是相同的。[1]
在微积分和数学分析中,像或这一类极限称为不定型。不定型是可以计算的,结果可能是任意数。

Remove ads
代数处理
若某数学系统遵从域的公理,则在该数学系统内除以零必须为没有意义。这是因为除法被定义为是乘法的逆向操作,即值是方程中的解(若有的话)。若设,方程式可写成或直接。因此,方程式没有解(当时),但是任何数值也可解此方程(当时)。在各自情况下均没有独一无二的数值,所以未能下定义。
在代数运算中不当使用除以零可得出无效证明:
式:
试:
- :正确
- :正确
得出:
除以零得出
简化,得出:
以上谬论假设,某数除以0是容许的,并且。
另一个简洁的证明
| 设,则两边同时减去,由平方差公式得两边除以,故。 |
通过上面的过程,证明了一切数字等于。此谬论是由于简化的过程不正确,计算过程使用了“除以零”。
因为是零,所以不能够把左右两边的删去。
Remove ads
Remove ads
数学分析
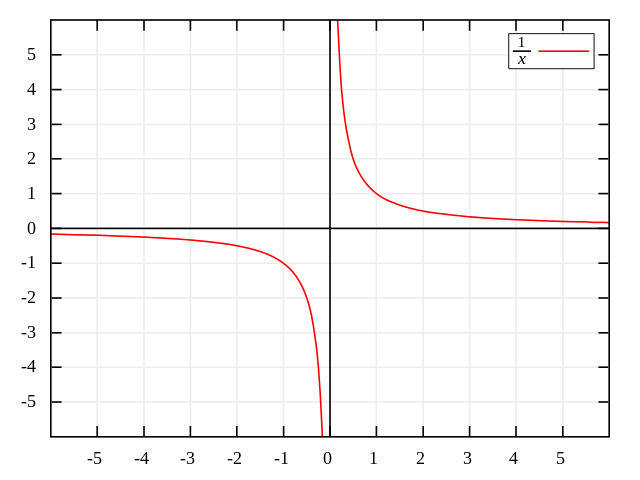
表面看来,可以借着考虑随着趋向的来定义“除以零”。
对于任何正数,右极限是
另一方面,左极限是
由于左极限及右极限不相同,因此函数在的极限不存在,该点没有定义。同样地,若是负数,极限也不存在。
如果分子及分母均为零或趋向零,则可使用洛必达法则计算。
Remove ads
不定型(Indeterminate Form)的极限可透过四则运算或洛必达法则计算。
考虑函数
如果直接代入,会得到零除以零,这是没有意义的。
但透过约简分子及分母,该点的极限是可以计算的。
此外,函数的极限可透过洛必达法则计算。
若随着趋向,与均趋向,该极限可等于任何实数或无限,或者根本不存在,视乎及是何函数。
Remove ads
运用形式推算,正号、负号或没有正负号因情况而定,除以零定义为:
计算机科学
在计算机中,除以零的结果根据编程语言、软硬件环境、数据类型、数值而不同。部分语言中,无论是整数还是浮点数,除以0均会产生异常,而在另一部分语言中,整数除以零会产生异常或未定义行为,而浮点数除以零的结果如下:
Remove ads
注释
参考
延伸阅读
参见
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads


























































