函子
来自维基百科,自由的百科全书
在范畴论中,函子是范畴间的一类映射。函子也可以解释为小范畴范畴内的态射。
函子首先现身于代数拓扑学,其中拓扑空间的连续映射给出相应的代数对象(如基本群、同调群或上同调群)的代数同态。在当代数学中,函子被用来描述各种范畴间的关系。“函子”(英文:Functor)一词借自哲学家鲁道夫·卡尔纳普的用语[1]。卡尔纳普使用“函子”这一词和函数之间的相关来类比谓词和性质之间的相关[2]。对卡尔纳普而言,不同于当代范畴论的用法,函子是个语言学的词汇。对范畴论者来说,函子则是个特别类型的函数。
定义
设C和D为范畴,从C至D的函子为一映射:
- 将每个对象映射至一对象上,
- 将每个态射映射至一态射上,使之满足下列条件:
- 对任何对象,恒有。
- 对任何态射,恒有。换言之,函子会保持单位态射与态射的复合。
一个由一范畴映射至其自身的函子称之为“自函子”。
数学中有许多构造具有函子的性质,不同之处在于它们将态射的方向“反转”。为此,我们定义反变函子 为:
- 将每个对象映射至一对象上。
- 将每个态射映射至一态射上。
使之满足:
- 对任何对象恒有。
- 对任何中的态射,恒有。
注意,反变函子反转了复合的方向。
在此脉络下,原定义中的函子亦称之为协变函子,以区分和反变函子之间的不同。也可以将反变函子定义为在对偶范畴上的“协变”函子。一些作者即较喜好将所有的表示式写成协变的。亦即,不说为一反变函子,而简单写成(或有时为),并称之为函子。
自然变换
两个函子间的自然变换是一族态射
使得任何及态射均满足下述交换图:
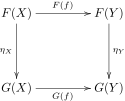
当皆为同构时,可以定义此自然变换之逆,两者的合成为恒等自然变换。此时称为函子之间的同构。
对反变函子也可以类似地定义自然变换。
例子
常数函子:将每个对象映射至一固定对象中,并将所有态射映射至中的函子C → D。常数函子亦之称为选择函子。
对角函子:对角函子被定义为由D至函子范畴DC的函子,将每个在D内的对象映射至此对象的常数函子上。
极限函子:对一固定的指标范畴,若每个函子J→C都有个极限(即若C为完全的),则极限函子CJ→C即为将每个函子映射至其极限的函子。此类函子的存在性可以由将其理解为对角函子的右伴随函子,且引入福端伴随函子定理来证明之。这需要一个适当版本的选择公理。相似的说法也可应用在上极限函子(其为协变的)之中。
幂集合:幂集合函子P : Set → Set将每个集合映射至其幂集合,且将每个函数映射至从至其值域的映射。亦可考虑反变幂集合函子,将f 映射至从U映射至其在Y内的逆象。
对偶向量空间:此函子将每个向量空间映射至其对偶空间中,并将每个线性映射映射至其对偶映射中,为一个由所有在一固定体上的向量空间所组成的范畴映射至其自身的反变函子。
基本群:考虑一个由有点空间(即带有可区分点的拓朴空间)所组成的范畴,其对象为对 (X, x0),其中X为一拓朴空间且x0为X中的一点,由 (X,x0)至 (Y, y0)的态射为一连续映射f : X → Y,且满足f(x0) = y0。
对每个有可区分点x0的拓朴空间X,可定义一个基于x0上的基本群π1(X, x0)。这个一个基于x0上的环的同伦类的群。若f : X → Y是一个有点空间的态射,则每个在X内,基于点x0上的环即可经由f得出一个在Y内,基于y0的环。此一运算和同伦等价关系及环的复合相符,故可得出一个由π(X, x0)至π(Y, y0)的群同态。因此,即可得出一个由有点拓朴空间范畴至群范畴的函子。
在拓朴空间(没有可区分点)范畴中,可考虑一般曲线的同伦类,但无法复合,除非它们共有一个端点。因此可以有一基本广群,而无法一定有一基本群。
连续函数的代数:一个由拓朴空间的范畴(其态射为连续映射)至实结合代数的范畴的反变函子,其将每个拓朴空间X映射至此空间上所有实变连续函数的代数C(X)上。每个连续映射f : X → Y都可导出一个代数同态C(f) : C(Y) → C(X),经由让每个C(Y)内的&phi,C(f)(φ) = φ o f。当空间带有更多结构(例如光滑流形、复流形)时,定义可以相应地推广。
切丛和馀切丛:将每个微分流形映射至其切丛中且将每个光滑映射映射至其导数中的映射,为一由微分流形的范畴至向量丛的范畴的协变函子。同样地,将每个微分流形映射至其馀切丛中且将每个光滑映射映射至其回拉的映射,为一反变函子。
在每个点上做此建构可以给出由有点微分流分的范畴至实向量空间的范畴的协变及反变函子。
群作用/表示:每个群G都可以被认为带有单一个对象的范畴。一个由G至Set的函子只是G在一特定集合上的群作用,即一个G-集合。同样地,一个由G至向量空间范畴VectK的函子会是个G的线性表示。一般来说,一个函子G → C可以被认为是G在范畴C中的一个对象上的“作用”。
李代数:将每个实(复)李群映射至其实(复)李代数可定义出一函子。
张量积:若C为在一固定体上的向量空间的范畴且其态射为线性映射,则张量积可定义出一个函子C × C → C,其中两个引数都是协变的。
遗忘函子:函子U : Grp → Set将群映射至其源集合且将群同态映射至其源函数。此类的函子会“遗忘”部份的结构,因此称之为“遗忘函子”。另一个例子为函子Rng → Ab,其将环映射至其源加法阿贝尔群中。在Rng中的态射(环同态)则遗忘了其中的乘法,而变成了在Ab中的态射(阿贝尔群同态)。其他如体、模、拓朴空间等基于集合的结构也可以取其遗忘函子。
自由函子:遗忘函子的反向即为自由函子。自由函子F : Set → Grp将每个集合X映射至由X产生的自由群,函数则映射至自由群间的群同态。自由函子的建构可存在于许多基于由集合的结构的范畴。详见自由对象。
同态群:对每一对群A、B,皆可得出一个由所有从A至B的群同态所组成的阿贝尔群Hom(A,B)。这是一个其第一个引数为反变,第二个引数为协变的函子,即为一函子Abop × Ab → Ab(其中的Ab为具群同态的阿贝尔群范畴)。若f : A1 → A2且g : B1 → B2为两个在Ab中的态射,则群同态Hom(f,g) : Hom(A2,B1) → Hom(A1,B2)以φ g o φ o f来给定。详见同态函子。
表示函子:可将上述例子广义化至任一范畴C中。即对每一对在C中的对象X、Y,可得出一个由从X至Y的所有态射所组成的集合Hom(X,Y)。这会定义出一个映射至Set,且其第一个引数为反变,第二个引数为协变的函子,即一函子Cop × C → Set。若f : X1 → X2且g : Y1 → Y2为C中的态射,则其群同态Hom(f,g) : Hom(X2,Y1) → Hom(X1,Y2)以φ g o φ o f来给定。
此类函子即称之为表示函子。建构出此函子的一个重要目的在于决定一给定函子是否为可表示的。
预层:若X为一拓扑空间,则在X上的开集会形成一个在包括下的偏序集合Open(X)。如同每个偏序开集一般,Open(X)会形成一个小范畴,带有态射U → V若且唯若时。在Open(X)上的反变函子称之为在X上的“预层”。例如,将每个开集U赋值至在U上的实变连续函数的结合代数,即可得到一个在X上的代数的顶层。
性质
从函子的公理中可得出两个重要的推论:
若函子满足为同构若且唯若为同构,则称之为保守函子。
在任意范畴C上,可定义一个单位函子1C,其将每个对象和态射映射至其自身。也可以将函子复合,即若F为一由A至B的函子且G为一由B至C的函子,则可组成一个由A至C的复合函子。函子的复合依定义是可结合的。这显示函子可以被认为是范畴的范畴中的态射。
一个只具单一对象的小范畴等同于一个幺半群,此一单一对象范畴的态射可被视为是幺半群中的元素,且其在范畴中的复合则可以视为是幺半群中的运算。此时这类范畴间的函子无非是幺半群间的同态。在此意义下,任意范畴间的函子可被视为是幺半群同态至多于一个对象的范畴的一种广义化。
双函子与多函子
双函子是函子概念在“双变元”时的推广。形式的定义则定义在两个范畴的积上的函子。
函子是一个自然的例子,它对第一个变元反变,对第二个变元协变。
双函子是有“两个”引数的函子。同态函子即为一个例子;其第一个引数为反变的,第二个引数则为协变的。
形式上来说,双函子是一个其定义域为积范畴的函子。例子,同态函子即为Cop × C → Set。
多函子是将函子的概念广义化至n个引数。而双函子当然是一个n=2的多函子。
与其他范畴论概念的关系
函子本身亦可视为函子范畴中的对象,该范畴中的态射是函子间的自然变换。近来有以“函子的态射”取代术语“自然变换”的趋势。
函子也经常以泛性质定义,例子包括了张量积,模或群的直和、直积,自由群与自由模的构造;许多构造可以统合于正极限与逆极限的概念下。
泛建构也往往给出一对伴随函子。
具特殊性质之函子
注释
Wikiwand - on
Seamless Wikipedia browsing. On steroids.













































