双曲函数

在数学中，双曲函数是一类与常见的三角函数（也叫圆函数）类似的函数。最基本的双曲函数是双曲正弦函数${\displaystyle \sinh }$和双曲馀弦函数${\displaystyle \cosh }$，从它们可以导出双曲正切函数${\displaystyle \tanh }$等，其推导也类似于三角函数的推导。双曲函数的反函数称为反双曲函数。

射线出原点交单位双曲线${\displaystyle x^{2}-y^{2}=1}$于点${\displaystyle (\cosh a,\sinh a)}$，这里的${\displaystyle a}$是射线、双曲线和x轴围成的面积的二倍。对于双曲线上位于x轴下方的点，这个面积被认为是负值

双曲函数示意图

几个双曲函数的图形。

双曲函数的定义域是实数，其自变量的值叫做双曲角。双曲函数出现于某些重要的线性微分方程的解中，譬如说定义悬链线和拉普拉斯方程。

基本定义

sinh、cosh和tanh

csch、sech和coth

最简单的几种双曲函数为^[1]：

• 双曲正弦：

  ${\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}}$

• 双曲馀弦：

  ${\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}}$

• 双曲正切：

  ${\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}.}$

• 双曲馀切：当${\displaystyle x\neq 0}$

  ${\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}.}$

• 双曲正割：

  ${\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}.}$

• 双曲馀割：当${\displaystyle x\neq 0}$

  ${\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}.}$

函数${\displaystyle \cosh x}$是关于y轴对称的偶函数。函数${\displaystyle \sinh x}$是奇函数。

如同当${\displaystyle t}$遍历实数集${\displaystyle \mathbb {R} }$时，点（${\displaystyle \cos t}$, ${\displaystyle \sin t}$）的轨迹是一个圆${\displaystyle x^{2}+y^{2}=1}$一样，当${\displaystyle t}$遍历实数集${\displaystyle \mathbb {R} }$时，点（${\displaystyle \cosh t}$, ${\displaystyle \sinh t}$）的轨迹是单位双曲线（英语：Unit hyperbola）${\displaystyle x^{2}-y^{2}=1}$的右半边。这是因为有以下的恒等式：

${\displaystyle \cosh ^{2}t-\sinh ^{2}t=1}$

参数t不是圆角而是双曲角，它表示在x轴和连接原点和双曲线上的点（${\displaystyle \cosh t}$, ${\displaystyle \sinh t}$）的直线之间的面积的两倍。

历史

在直角双曲线（方程${\displaystyle y={1 \over x}}$）下，双曲线三角形（黄色），和对应于双曲角u的双曲线扇形（红色）。这个三角形的边分别是双曲函数中${\displaystyle \cosh }$和${\displaystyle \sinh }$的${\displaystyle {\sqrt {2}}}$倍。

在18世纪，约翰·海因里希·兰伯特引入双曲函数^[2]，并计算了双曲几何中双曲三角形的面积^[3]。自然对数函数是在直角双曲线${\displaystyle xy=1}$下定义的，可构造双曲线直角三角形，底边在线${\displaystyle y=x}$上，一个顶点是原点，另一个顶点在双曲线。这里以自然对数即双曲角作为参数的函数，是自然对数的逆函数指数函数，即要形成指定双曲角${\displaystyle u}$，在渐近线即x或y轴上需要有的${\displaystyle x}$或${\displaystyle y}$的值。显见这里的底边是${\displaystyle \left(e^{u}+e^{-u}\right){\frac {\sqrt {2}}{2}}}$，垂线是${\displaystyle \left(e^{u}-e^{-u}\right){\frac {\sqrt {2}}{2}}}$。

通过旋转和缩小线性变换，得到单位双曲线下的情况，有：

• ${\displaystyle \cosh u={\frac {e^{u}+e^{-u}}{2}}}$
• ${\displaystyle \sinh u={\frac {e^{u}-e^{-u}}{2}}}$

单位双曲线中双曲线扇形的面积是对应直角双曲线${\displaystyle xy=1}$下双曲角的${\displaystyle {1 \over 2}}$。

虚数圆角定义

双曲角经常定义得如同虚数圆角。实际上，如果${\displaystyle x}$是实数而${\displaystyle i^{2}=-1}$，则

${\displaystyle \cos(ix)=\cosh(x),\quad }$ ${\displaystyle -i\sin(ix)=\sinh(x).}$

所以双曲函数${\displaystyle \cosh }$和${\displaystyle \sinh }$可以通过圆函数来定义。这些恒等式不是从圆或旋转得来的，它们应当以无穷级数的方式来理解。特别是，可以将指数函数表达为由偶次项和奇次项组成，前者形成${\displaystyle \cosh }$函数，后者形成了${\displaystyle \sinh }$函数。${\displaystyle \cos }$函数的无穷级数可从${\displaystyle \cosh }$得出，通过把它变为交错级数，而${\displaystyle \sin }$函数可来自将${\displaystyle \sinh }$变为交错级数。上面的恒等式使用虚数${\displaystyle i}$，从三角函数的级数的项中去掉交错因子${\displaystyle (-1)^{n}}$，来恢复为指数函数的那两部份级数。

${\displaystyle e^{x}=\cosh x+\sinh x\!}$

${\displaystyle {\begin{array}{lcl}\cosh x=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&\sinh x=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}\\\cos x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}&\sin x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}\\\end{array}}}$

双曲函数可以通过虚数圆角定义为：

• 双曲正弦：^[1]

  ${\displaystyle \sinh x=-i\sin(ix)\!}$

• 双曲馀弦：^[1]

  ${\displaystyle \cosh x=\cos(ix)\!}$

• 双曲正切：

  ${\displaystyle \tanh x=-i\tan(ix)\!}$

• 双曲馀切：

  ${\displaystyle \coth x=i\cot(ix)\!}$

• 双曲正割：

  ${\displaystyle \operatorname {sech} x=\sec(ix)\!}$

• 双曲馀割：

  ${\displaystyle \operatorname {csch} x=i\csc(ix)\!}$

这些复数形式的定义得出自欧拉公式。

与三角函数的类比

奥古斯都·德·摩根在其1849年出版的教科书《Trigonometry and Double Algebra》中将圆三角学扩展到了双曲线^[4]。威廉·金顿·克利福德在1878年使用双曲角来参数化单位双曲线。

给定相同的角α，在双曲线上计算双曲角的量值（双曲扇形面积除以半径）得到双曲函数，角${\displaystyle \alpha }$得到三角函数。在单位圆和单位双曲线上，双曲函数与三角函数有如下的关系:

• 正弦同样是从x轴到曲线的半弦。
• 馀弦同样是从y轴到曲线的半弦（图中的馀弦是长方形的另一条边）。
• 正切同样是过x轴上单位点（1,0）在曲线上的切线到终边的长度。
• 馀切同样是从y轴与过终边和曲线交点的切线与y轴的交点和曲线连线之长度。
• 正割同样是在一个有正切和单位长的直角三角形上，但边不一样。
• 馀割同样是y轴与过终边和曲线交点的切线与y轴的交点和原点之距离。
• 角的量值可以从0到无限大，但${\displaystyle \alpha }$实际上只会介于${\displaystyle 0}$到${\displaystyle 2\pi }$（360度）之间，其馀是${\displaystyle \alpha }$的同界角，再绕著圆旋转，故三角函数可以有周期。双曲角的量值可以从${\displaystyle 0}$到无限大，但${\displaystyle \alpha }$实际上不会超过${\displaystyle {\frac {\pi }{4}}}$（45度），故无法如三角函数一样有周期性。

恒等式

主条目：双曲函数恒等式

与双曲函数有关的恒等式如下:

${\displaystyle {\begin{aligned}\cosh ^{2}x-\sinh ^{2}x=1\\1-\tanh ^{2}x=\operatorname {sech} ^{2}x\\\operatorname {coth} ^{2}x-1=\operatorname {csch} ^{2}x\\\end{aligned}}}$

• 加法公式：

${\displaystyle \sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y}$

${\displaystyle \cosh(x+y)=\cosh x\cosh y+\sinh x\sinh y}$

${\displaystyle \tanh(x+y)={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}}$

• 二倍角公式：

${\displaystyle \sinh 2x\ =2\sinh x\cosh x}$

${\displaystyle \cosh 2x\ =\cosh ^{2}x+\sinh ^{2}x=2\cosh ^{2}x-1=2\sinh ^{2}x+1}$

${\displaystyle \tanh 2x={\frac {2\tanh x}{1+\tanh ^{2}x}}}$

• 和差化积：

${\displaystyle {\begin{aligned}\sinh x+\sinh y&=2\sinh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\cosh x+\cosh y&=2\cosh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\end{aligned}}}$

• 半角公式：

${\displaystyle \sinh {\frac {x}{2}}={\frac {\sinh x}{\sqrt {2(\cosh x+1)}}}=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}}$

${\displaystyle \cosh {\frac {x}{2}}={\sqrt {\frac {\cosh x+1}{2}}}}$

${\displaystyle \tanh {\frac {x}{2}}={\frac {\sinh x}{\cosh x+1}}=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}}$

其中 sgn 为符号函数。

若 x ≠ 0，则：

${\displaystyle \tanh {\frac {x}{2}}={\frac {\cosh x-1}{\sinh x}}=\coth x-\operatorname {csch} x}$

由于双曲函数和三角函数之间的对应关系，双曲函数的恒等式和三角函数的恒等式之间也是一一对应的。对于一个已知的三角函数公式，只需要将其中的三角函数转成相应的双曲函数，并将含有有两个${\displaystyle \sinh }$的积的项（包括${\displaystyle \coth ^{2}x,\tanh ^{2}x,\operatorname {csch} ^{2}x,\sinh x\sinh y}$）转换正负号，就可得到相应的双曲函数恒等式^[5]。如

• 三倍角公式：

三角函数的三倍角公式为：

${\displaystyle \sin 3x\ =3\sin x-4\sin ^{3}x}$

${\displaystyle \cos 3x\ =-3\cos x+4\cos ^{3}x}$

而对应的双曲函数三倍角公式则是：

${\displaystyle \sinh 3x\ =3\sinh x+4\sinh ^{3}x}$

${\displaystyle \cosh 3x\ =-3\cosh x+4\cosh ^{3}x}$

• 差角公式：

${\displaystyle {\begin{aligned}\sinh(x-y)&=\sinh x\cosh y-\cosh x\sinh y\\\cosh(x-y)&=\cosh x\cosh y-\sinh x\sinh y\\\tanh(x-y)&={\frac {\tanh x-\tanh y}{1-\tanh x\tanh y}}\\\end{aligned}}}$

双曲函数的导数

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\sinh x&=\cosh x\\{\frac {d}{dx}}\cosh x&=\sinh x\\{\frac {d}{dx}}\tanh x&=1-\tanh ^{2}x=\operatorname {sech} ^{2}x={\frac {1}{\cosh ^{2}x}}\\{\frac {d}{dx}}\coth x&=1-\coth ^{2}x=-\operatorname {csch} ^{2}x=-{\frac {1}{\sinh ^{2}x}}&&x\neq 0\\{\frac {d}{dx}}\operatorname {sech} x&=-\tanh x\operatorname {sech} x\\{\frac {d}{dx}}\operatorname {csch} x&=-\coth x\operatorname {csch} x&&x\neq 0\end{aligned}}}$

双曲函数的泰勒展开式

双曲函数也可以以泰勒级数展开:

${\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}$

${\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}$

${\displaystyle \tanh x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}$

${\displaystyle \coth x={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }$（罗朗级数）

${\displaystyle \operatorname {sech} \,x=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}$

${\displaystyle \operatorname {csch} \,x={\frac {1}{x}}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }$（罗朗级数）

其中

${\displaystyle B_{n}}$是第${\displaystyle n}$项伯努利数

${\displaystyle E_{n}}$是第${\displaystyle n}$项欧拉数

无限积与连续分数形式

下列的扩展在整个复数平面上成立：

${\displaystyle \sinh x=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{n^{2}\pi ^{2}}}\right)={\cfrac {x}{1-{\cfrac {x^{2}}{2\cdot 3+x^{2}-{\cfrac {2\cdot 3x^{2}}{4\cdot 5+x^{2}-{\cfrac {4\cdot 5x^{2}}{6\cdot 7+x^{2}-\ddots }}}}}}}}}$

${\displaystyle \cosh x=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{(n-1/2)^{2}\pi ^{2}}}\right)={\cfrac {1}{1-{\cfrac {x^{2}}{1\cdot 2+x^{2}-{\cfrac {1\cdot 2x^{2}}{3\cdot 4+x^{2}-{\cfrac {3\cdot 4x^{2}}{5\cdot 6+x^{2}-\ddots }}}}}}}}}$

${\displaystyle \tanh x={\cfrac {1}{{\cfrac {1}{x}}+{\cfrac {1}{{\cfrac {3}{x}}+{\cfrac {1}{{\cfrac {5}{x}}+{\cfrac {1}{{\cfrac {7}{x}}+\ddots }}}}}}}}}$

双曲函数的积分

${\displaystyle \int \sinh cx\,\mathrm {d} x={\frac {1}{c}}\cosh cx+C}$

${\displaystyle \int \cosh cx\,\mathrm {d} x={\frac {1}{c}}\sinh cx+C}$

${\displaystyle \int \tanh cx\,\mathrm {d} x={\frac {1}{c}}\ln(\cosh cx)+C}$

${\displaystyle \int \coth cx\,\mathrm {d} x={\frac {1}{c}}\ln \left|\sinh cx\right|+C}$

${\displaystyle \int \operatorname {sech} cx\,\mathrm {d} x={\frac {1}{c}}\arctan(\sinh cx)+C}$

${\displaystyle \int \operatorname {csch} cx\,\mathrm {d} x={\frac {1}{c}}\ln \left|\tanh {\frac {cx}{2}}\right|+C}$

与指数函数的关系

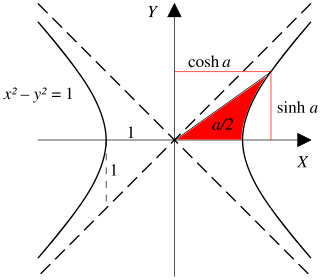
从双曲正弦和馀弦的定义，可以得出如下恒等式:

${\displaystyle e^{x}=\cosh x+\sinh x}$

和

${\displaystyle e^{-x}=\cosh x-\sinh x}$

复数的双曲函数

因为指数函数可以定义为任何复数参数，也可以扩展双曲函数的定义为复数参数。函数${\displaystyle \sinh z}$和${\displaystyle \cosh z}$是全纯函数。

指数函数与三角函数的关系由欧拉公式给出：

${\displaystyle {\begin{aligned}e^{ix}&=\cos x+i\;\sin x\\e^{-ix}&=\cos x-i\;\sin x\end{aligned}}}$

所以:

${\displaystyle {\begin{aligned}\cosh ix&={\frac {1}{2}}\left(e^{ix}+e^{-ix}\right)=\cos x\\\sinh ix&={\frac {1}{2}}\left(e^{ix}-e^{-ix}\right)=i\sin x\\\tanh ix&=i\tan x\\\end{aligned}}}$

${\displaystyle {\begin{aligned}\cosh(x+iy)&=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\\\sinh(x+iy)&=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\\\end{aligned}}}$

${\displaystyle {\begin{aligned}\cosh x&=\cos ix\\\sinh x&=-i\sin ix\\\tanh x&=-i\tan ix\end{aligned}}}$

因此，双曲函数是关于虚部有周期的，周期为${\displaystyle 2\pi i}$（对双曲正切和馀切是${\displaystyle \pi i}$）。

反双曲函数

主条目：反双曲函数

反双曲函数是双曲函数的反函数。它们的定义为：

${\displaystyle {\begin{aligned}\operatorname {arsinh} (x)&=\ln \left(x+{\sqrt {x^{2}+1}}\right)\\\operatorname {arcosh} (x)&=\ln \left(x+{\sqrt {x^{2}-1}}\right);x\geq 1\\\operatorname {artanh} (x)&={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right);\left|x\right|<1\\\operatorname {arcoth} (x)&={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right);\left|x\right|>1\\\operatorname {arsech} (x)&=\ln \left({\frac {1}{x}}+{\frac {\sqrt {1-x^{2}}}{x}}\right);0<x\leq 1\\\operatorname {arcsch} (x)&=\ln \left({\frac {1}{x}}+{\frac {\sqrt {1+x^{2}}}{\left|x\right|}}\right);x\neq 0\end{aligned}}}$

参考文献

1. Weisstein, Eric W. (编). Hyperbolic Functions. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2020-08-29]. （原始内容存档于2022-05-21） （英语）.
2. Eves, Howard, Foundations and Fundamental Concepts of Mathematics, Courier Dover Publications: 59, 2012, ISBN 9780486132204, We also owe to Lambert the first systematic development of the theory of hyperbolic functions and, indeed, our present notation for these functions.
3. Ratcliffe, John, Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics 149, Springer: 99, 2006 [2014-03-27], ISBN 9780387331973, （原始内容存档于2014-01-12）, That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786.
4. Augustus De Morgan (1849) Trigonometry and Double Algebra （页面存档备份，存于互联网档案馆）, Chapter VI: "On the connection of common and hyperbolic trigonometry"
5. G. Osborn, Mnemonic for hyperbolic formulae^{[失效链接]}, The Mathematical Gazette, p. 189, volume 2, issue 34, July 1902

参见

• 反双曲函数
• 双曲函数符号
• 三角函数
• 古德曼函数