在数学 里,希尔伯特空间 (英语:Hilbert space )即完备的内积空间 ,也就是一个带有内积 的完备 矢量空间。内积的构造推广了欧几里得空间 的距离 和角 的概念;完备则确保了其上所有的柯西序列 会收敛到此空间里的一点,从而微积分 中的许多概念都可以推广到希尔伯特空间中。
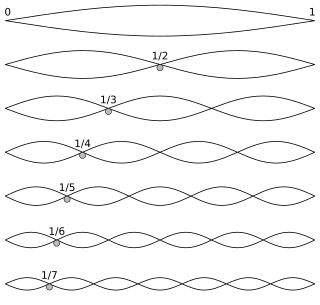
希尔伯特空间可以用来研究振动的弦的谐波。 希尔伯特空间为基于任意正交坐标系 上的多项式 表示的傅立叶级数 和傅立叶变换 提供了一种有效的表述方式,而这也是泛函分析 的核心概念之一。另外希尔伯特空间也是量子力学 的重要数学基础之一。
希尔伯特空间以大卫·希尔伯特 的名字命名,他在对积分方程 的研究中研究了希尔伯特空间。冯·诺伊曼 在其1929年出版的关于无界 自伴算子 的著作中[ 1] 量子力学 的基础性和创造性地研究的时候认识到了这一点。此项研究由冯·诺伊曼与希尔伯特[ 2] 朗道 展开,随后由尤金·维格纳 (Eugene Wigner )继续深入。“希尔伯特空间”这个名字迅速被其他科学家所接受,例如在外尔 1931年出版的著作《群与量子力学的理论》[ 3] The Theory of Groups and Quantum Mechanics )中就使用了这一名词。
一个抽象的希尔伯特空间中的元素往往被称为矢量 。在实际应用中,它可能代表了一列复数 或是一个函数 。例如在量子力学中,一个物理系统可以表示为一个复 希尔伯特空间,其中的矢量是描述系统可能状态的波函数 。详细的资料可以参考量子力学的数学表述 相关的内容。量子力学中由平面波 和束缚态所构成的希尔伯特空间,一般被称为装备希尔伯特空间 (rigged Hilbert space)
在所有的无穷维 拓扑矢量空间 中,希尔伯特空间性质最好,也最接近有限维空间的情形。例如
傅立叶分析 的一个重要目的是将一个给定的函数表示成一族给定的基底函数 的和(可能是无穷和)。这个问题可以在希尔伯特空间中更抽象地描述为:任何一个希尔伯特空间都有一族标准正交基 ,而且每个希尔伯特空间中的元素都可以唯一地表示为这族基底 中的元素或其倍数的和。
若在复(或实)内积空间
H
{\displaystyle H}
柯西序列 ,都收敛于
H
{\displaystyle H}
H
{\displaystyle H}
希尔伯特空间的定义 —
H
{\displaystyle H}
序列
{
v
i
∈
H
}
i
∈
N
{\displaystyle {\{v_{i}\in H\}}_{i\in \mathbb {N} }}
d
(
v
,
w
)
:=
‖
v
−
w
‖
=
⟨
v
−
w
,
v
−
w
⟩
{\displaystyle d(v,\,w):=\|v-w\|={\sqrt {\langle v-w,\,v-w\rangle }}}
内积空间#范数 )
“对所有的正实数
ϵ
>
0
{\displaystyle \epsilon >0}
正整数
n
∈
N
{\displaystyle n\in \mathbb {N} }
i
,
j
∈
N
{\displaystyle i,\,j\in \mathbb {N} }
i
,
j
>
n
{\displaystyle i,\,j>n}
d
(
v
i
,
v
j
)
<
ϵ
{\displaystyle d(v_{i},\,v_{j})<\epsilon }
时,就存在矢量
v
∈
H
{\displaystyle v\in H}
“对所有的正实数
ϵ
>
0
{\displaystyle \epsilon >0}
n
∈
N
{\displaystyle n\in \mathbb {N} }
i
,
∈
N
{\displaystyle i,\in \mathbb {N} }
i
>
n
{\displaystyle i>n}
d
(
v
i
,
v
)
<
ϵ
{\displaystyle d(v_{i},\,v)<\epsilon }
这时称
H
{\displaystyle H}
希尔伯特空间 (Hilbert space)。
勒贝格空间 ( 这里指
L
2
(
X
)
{\displaystyle L^{2}(X)}
测度空间
(
X
,
M
,
μ
)
{\displaystyle (X,{\mathcal {M}},\mu )}
函数空间 ,其中
X
{\displaystyle X}
M
{\displaystyle {\mathcal {M}}}
X
{\displaystyle X}
σ
{\displaystyle \sigma }
M
{\displaystyle {\mathcal {M}}}
μ
{\displaystyle \mu }
M
{\displaystyle {\mathcal {M}}}
测度 。
更仔细的说,
L
2
(
X
,
μ
)
{\displaystyle L^{2}(X,\mu )}
L
2
(
X
)
{\displaystyle L^{2}(X)}
X
{\displaystyle X}
平方可积 (square-integrable)的复数值的可测函数 的集合。平方可积 表示该函数的绝对值 的平方的积分 是有限 的。要注意的是在
L
2
(
X
)
{\displaystyle L^{2}(X)}
函数 ,也就是说如果两函数只在一个测度 为0的集合上不相等,我们把这两函数当做在
L
2
(
X
)
{\displaystyle L^{2}(X)}
此时两个函数
f
{\displaystyle f}
g
{\displaystyle g}
内积 定义为
⟨
f
,
g
⟩
=
∫
X
f
(
t
)
¯
g
(
t
)
d
μ
(
t
)
{\displaystyle \langle f,g\rangle =\int _{X}{\overline {f(t)}}g(t)\ d\mu (t)}
因为
f
,
g
∈
L
2
(
X
)
{\displaystyle f,g\in L^{2}(X)}
但需要证明的是:
这个证明可以在相关的书籍中找到,与此例相关的内容可以参看关于
L
p
{\displaystyle L^{p}}
索伯列夫空间 一般表示为
H
s
{\displaystyle H^{s}}
W
s
,
2
{\displaystyle W^{s,2}}
偏微分方程 的研究。
More information 若复内积空间
证明
若复内积空间
V
{\displaystyle V}
N
{\displaystyle N}
格拉姆-施密特正交化 ,存在一列矢量:
{
e
1
,
e
2
,
…
,
e
N
}
{\displaystyle \{e_{1},\,e_{2},\,\ldots ,\,e_{N}\}}
为
V
{\displaystyle V}
正交 基底 ,现在假设
{
v
i
∈
V
}
i
∈
N
{\displaystyle {\{v_{i}\in V\}}_{i\in \mathbb {N} }}
柯西序列 ,换句话说:
“对所有的正实数
ϵ
>
0
{\displaystyle \epsilon >0}
正整数
n
∈
N
{\displaystyle n\in \mathbb {N} }
i
,
j
∈
N
{\displaystyle i,\,j\in \mathbb {N} }
i
,
j
>
n
{\displaystyle i,\,j>n}
d
(
v
i
,
v
j
)
<
ϵ
{\displaystyle d(v_{i},\,v_{j})<\epsilon }
这样,对每个正整数
i
∈
N
{\displaystyle i\in \mathbb {N} }
复数
z
i
1
,
z
i
2
,
…
,
z
i
N
∈
C
{\displaystyle z_{i1},\,z_{i2},\,\ldots ,\,z_{iN}\in \mathbb {C} }
v
i
=
∑
k
=
1
N
z
i
k
⋅
e
k
{\displaystyle v_{i}=\sum _{k=1}^{N}z_{ik}\cdot e_{k}}
这样根据内积空间的勾股定理 有
[
d
(
v
i
,
v
j
)
]
2
=
∑
k
=
1
N
|
z
i
k
−
z
j
k
|
2
<
ϵ
2
{\displaystyle {[d(v_{i},\,v_{j})]}^{2}=\sum _{k=1}^{N}{|z_{ik}-z_{jk}|}^{2}<\epsilon ^{2}}
取
x
i
k
=
Re
(
z
i
k
)
{\displaystyle x_{ik}=\operatorname {Re} (z_{ik})}
y
i
k
=
Im
(
z
i
k
)
{\displaystyle y_{ik}=\operatorname {Im} (z_{ik})}
∑
k
=
1
N
|
z
i
k
−
z
j
k
|
2
=
∑
k
=
1
N
|
x
i
k
−
x
j
k
|
2
+
∑
k
=
1
N
|
y
i
k
−
y
j
k
|
2
<
ϵ
2
{\displaystyle \sum _{k=1}^{N}{|z_{ik}-z_{jk}|}^{2}=\sum _{k=1}^{N}{|x_{ik}-x_{jk}|}^{2}+\sum _{k=1}^{N}{|y_{ik}-y_{jk}|}^{2}<\epsilon ^{2}}
所以
|
x
i
k
−
x
j
k
|
<
ϵ
{\displaystyle {|x_{ik}-x_{jk}|}<\epsilon }
|
y
i
k
−
y
j
k
|
<
ϵ
{\displaystyle {|y_{ik}-y_{jk}|}<\epsilon }
这样的话,对每个正整数
k
∈
N
{\displaystyle k\in \mathbb {N} }
实数 数列
{
x
i
k
∈
R
}
i
∈
N
{\displaystyle {\{x_{ik}\in \mathbb {R} \}}_{i\in \mathbb {N} }}
{
y
i
k
∈
R
}
i
∈
N
{\displaystyle {\{y_{ik}\in \mathbb {R} \}}_{i\in \mathbb {N} }}
实数完备性 ,存在唯一的
x
k
∈
R
{\displaystyle x_{k}\in \mathbb {R} }
y
k
∈
R
{\displaystyle y_{k}\in \mathbb {R} }
lim
i
→
∞
x
i
k
=
x
k
{\displaystyle \lim _{i\to \infty }x_{ik}=x_{k}}
lim
i
→
∞
y
i
k
=
y
k
{\displaystyle \lim _{i\to \infty }y_{ik}=y_{k}}
那这样根据数列极限 的定义,对每个正整数
k
∈
N
{\displaystyle k\in \mathbb {N} }
ϵ
>
0
{\displaystyle \epsilon >0}
n
1
,
n
2
,
…
,
n
2
N
∈
N
{\displaystyle n_{1},\,n_{2},\,\ldots ,\,n_{2N}\in \mathbb {N} }
i
∈
N
{\displaystyle i\in \mathbb {N} }
i
>
max
{
n
1
,
n
2
,
…
,
n
2
N
}
{\displaystyle i>\max\{n_{1},\,n_{2},\,\ldots ,\,n_{2N}\}}
|
x
i
k
−
x
k
|
<
ϵ
2
N
{\displaystyle {|x_{ik}-x_{k}|}<{\frac {\epsilon }{\sqrt {2N}}}}
|
y
i
k
−
y
k
|
<
ϵ
2
N
{\displaystyle {|y_{ik}-y_{k}|}<{\frac {\epsilon }{\sqrt {2N}}}}
这样的话,取
z
k
=
x
k
+
i
y
k
{\displaystyle z_{k}=x_{k}+iy_{k}}
v
=
∑
k
=
1
N
z
k
⋅
e
k
{\displaystyle v=\sum _{k=1}^{N}z_{k}\cdot e_{k}}
[
d
(
v
i
,
v
)
]
2
=
∑
k
=
1
N
|
x
i
k
−
x
k
|
2
+
∑
k
=
1
N
|
y
i
k
−
y
k
|
2
<
ϵ
2
{\displaystyle {[d(v_{i},\,v)]}^{2}=\sum _{k=1}^{N}{|x_{ik}-x_{k}|}^{2}+\sum _{k=1}^{N}{|y_{ik}-y_{k}|}^{2}<\epsilon ^{2}}
换句话说:
lim
i
→
∞
v
i
=
v
{\displaystyle \lim _{i\to \infty }v_{i}=v}
这样就证明了
V
{\displaystyle V}
V
{\displaystyle V}
V
{\displaystyle V}
◻
{\displaystyle \Box }
Close
H
{\displaystyle H}
v
∈
H
{\displaystyle v\in H}
函数
f
(
h
)
=
⟨
v
,
h
⟩
(
h
∈
H
)
{\displaystyle f(h)=\langle v,h\rangle \;(h\in H)}
τ
H
{\displaystyle \tau _{H}}
τ
R
{\displaystyle \tau _{\mathbb {R} }}
连续 函数
f
(
h
)
=
⟨
h
,
h
⟩
(
h
∈
H
)
{\displaystyle f(h)=\langle h,h\rangle \;(h\in H)}
τ
H
{\displaystyle \tau _{H}}
τ
R
{\displaystyle \tau _{\mathbb {R} }}
连续 More information 证明 ...
Close
在希尔伯特空间 H {xn } v ∈ H
lim
n
⟨
x
n
,
v
⟩
=
⟨
x
,
v
⟩
,
{\displaystyle \lim _{n}\langle x_{n},v\rangle =\langle x,v\rangle ,}
则称该序列弱收敛 x ∈ H .
例如,任何正交序列 {fn } 贝塞尔不等式 的结果。根据一致有界原理 ,每个弱收敛序列 {xn }
反之,希尔伯特空间中的每个有界序列,都有一个弱收敛子序列,此谓巴拿赫-阿拉奥卢定理 。[ 4] 凸泛函 的最小值的存在性,正如波尔查诺-魏尔斯特拉斯定理 适用于 ℝ d [ 5]
若 f : H → ℝ ‖x ‖ ∞ f (x )+∞ f x 0 ∈ H 此个结论(并其若干推广)是变分法 中直接法 H 弱紧集 (因为 H Eberlein–Šmulian theorem
在希尔伯特空间 H u v ⟨ u ,v ⟩ = 0u ⊥ v S H u ⊥ S u S
当 u v
‖
u
+
v
‖
2
=
⟨
u
+
v
,
u
+
v
⟩
=
⟨
u
,
u
⟩
+
2
Re
⟨
u
,
v
⟩
+
⟨
v
,
v
⟩
=
‖
u
‖
2
+
‖
v
‖
2
.
{\displaystyle \|u+v\|^{2}=\langle u+v,u+v\rangle =\langle u,u\rangle +2\,\operatorname {Re} \langle u,v\rangle +\langle v,v\rangle =\|u\|^{2}+\|v\|^{2}\,.}
对 n n u 1 , ..., un
‖
u
1
+
⋯
+
u
n
‖
2
=
‖
u
1
‖
2
+
⋯
+
‖
u
n
‖
2
.
{\displaystyle \|u_{1}+\cdots +u_{n}\|^{2}=\|u_{1}\|^{2}+\cdots +\|u_{n}\|^{2}\,.}
毕达哥拉斯恒等式对每个内积空间都成立,但希尔伯特空间具有完备性,故此恒等式可推广到对级数成立。一列 正交 矢量组成的级数 ∑uk H
‖
∑
k
=
0
∞
u
k
‖
2
=
∑
k
=
0
∞
‖
u
k
‖
2
.
{\displaystyle \left\|\sum _{k=0}^{\infty }u_{k}\right\|^{2}=\sum _{k=0}^{\infty }\left\|u_{k}\right\|^{2}\,.}
此外,正交矢量的级数和与求和顺序无关。
几何上,平行四边形恒等式给出 AC2 + BD2 = 2(AB2 + AD2 ) 由定义,每个希尔伯特空间都是巴拿赫空间 。 而在每个希尔伯特空间中,以下平行四边形恒等式 成立:
‖
u
+
v
‖
2
+
‖
u
−
v
‖
2
=
2
(
‖
u
‖
2
+
‖
v
‖
2
)
.
{\displaystyle \|u+v\|^{2}+\|u-v\|^{2}=2\left(\|u\|^{2}+\|v\|^{2}\right)\,.}
反之,若一个巴拿赫空间满足平行四边形恒等式,则其亦为希尔伯特空间,因为它的内积可由极化恒等式 唯一确定。[ 6]
⟨
u
,
v
⟩
=
1
4
(
‖
u
+
v
‖
2
−
‖
u
−
v
‖
2
)
.
{\displaystyle \langle u,v\rangle ={\tfrac {1}{4}}\left(\|u+v\|^{2}-\|u-v\|^{2}\right)\,.}
而对复希尔伯特空间,其为
⟨
u
,
v
⟩
=
1
4
(
‖
u
+
v
‖
2
−
‖
u
−
v
‖
2
+
i
‖
u
+
i
v
‖
2
−
i
‖
u
−
i
v
‖
2
)
.
{\displaystyle \langle u,v\rangle ={\tfrac {1}{4}}\left(\|u+v\|^{2}-\|u-v\|^{2}+i\|u+iv\|^{2}-i\|u-iv\|^{2}\right)\,.}
由平行四边形恒等式,可以推出任何希尔伯特空间都是一致凸巴拿赫空间 [ 7]
根据希尔伯特射影定理 C H x H y ∈ C x C x [ 8]
y
∈
C
,
‖
x
−
y
‖
=
dist
(
x
,
C
)
=
min
{
‖
x
−
z
‖
:
z
∈
C
}
.
{\displaystyle y\in C\,,\quad \|x-y\|=\operatorname {dist} (x,C)=\min\{\|x-z\|:z\in C\}\,.}
此等价于经平移的凸集 D = C − x (dn ) ⊂ D D D [ 9]
当对 H F x y ∈ F [ 10]
y
∈
F
,
x
−
y
⊥
F
.
{\displaystyle y\in F\,,\quad x-y\perp F\,.}
该点 y x F 正交射影 ,而这给出的映射 PF : x ↦ y 应用数学 有用,而数值分析 尤甚,因这结论是最小二乘法 的基础。 [ 11]
特别到,当 F H v F x ∉ F v = x − y
H S 0 H S
对偶空间 H *H 连续 线性函数组成的空间。 其具有一个自然的范数,由下式给出:
‖
φ
‖
=
sup
‖
x
‖
=
1
,
x
∈
H
|
φ
(
x
)
|
.
{\displaystyle \|\varphi \|=\sup _{\|x\|=1,x\in H}|\varphi (x)|\,.}
这满足平行四边形恒等式,故对偶空间亦为一个内积空间。同时它也是完备的,所以希尔伯特空间的对偶空间也是希尔伯特空间。
里斯表示定理 描述了这个对偶空间。 对每个 H u H *φu
φ
u
(
x
)
=
⟨
x
,
u
⟩
.
{\displaystyle \varphi _{u}(x)=\langle x,u\rangle \,.}
则 u ↦ φu H H *反线性映射 。里斯表示定理说此映射是个反线性同构。 [ 12] H *φ uφ ∈ H
⟨
x
,
u
φ
⟩
=
φ
(
x
)
{\displaystyle \langle x,u_{\varphi }\rangle =\varphi (x)}
对任意 x ∈ H H *
⟨
φ
,
ψ
⟩
=
⟨
u
ψ
,
u
φ
⟩
.
{\displaystyle \langle \varphi ,\psi \rangle =\langle u_{\psi },u_{\varphi }\rangle \,.}
注意右边的次序反转了,才使 uφ φ H H 自然 地与其对偶同构。
表示 φ uφ φ ≠ 0核 F = Ker(φ )H H v F u v λv φ (v ) = ⟨v ,u ⟩
u
=
⟨
v
,
v
⟩
−
1
φ
(
v
)
¯
v
.
{\displaystyle u=\langle v,v\rangle ^{-1}\,{\overline {\varphi (v)}}\,v\,.}
物理学 上广泛应用的狄拉克符号 正利用了φ ↔ u ⟨ x |y ⟩
⟨
x
|
y
⟩
=
⟨
y
,
x
⟩
.
{\displaystyle \langle x|y\rangle =\langle y,x\rangle \,.}
于是 ⟨ x |y ⟩ ⟨ x |左矢 )作用在矢量 |y ⟩ 右矢 )的结果。
里斯表示定理要求空间的完备性。事实上,从定理可知任意内积空间的拓扑对偶都与其完备化空间同构。作为里斯表示定理的直接推论, 希尔伯特空间 H 自反空间 , 即由 H
希尔伯特空间的一个中间概念是标准正交基 ,即其上的一族函数
{
e
k
}
k
∈
B
{\displaystyle \{e_{k}\}_{k\in B}}
所有元素都是单位化 的:即对于任意
x
{\displaystyle x}
‖
e
k
‖
=
1
{\displaystyle \Vert e_{k}\Vert =1}
∀
k
∈
B
{\displaystyle \forall k\in B}
所有元素彼此正交 :若
x
{\displaystyle x}
y
{\displaystyle y}
<
x
,
y
>=
0
{\displaystyle <x,y>=0}
其线性扩张稠密:即其中的所有元素的有限的线性组合 是
H
{\displaystyle H}
稠密子集 。 有时也使用标准正交列 或标准正交集 指代。
标准正交基的一些实例:
集合 (
{
(
1
,
0
,
0
)
,
(
0
,
1
,
0
)
,
(
0
,
0
,
1
)
}
{\displaystyle \{(1,0,0),(0,1,0),(0,0,1)\}}
给定任意两个(或更多)希尔伯特空间,利用直和 或张量积 的方式,可以给出一个更大的希尔伯特空间。
Von Neumann, John . Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren. Mathematische Annalen. 1929, 102 : 49–131.Blanchet, Gérard; Charbit, Maurice. Digital Signal and Image Processing Using MATLAB. Digital Signal and Image Processing 1 Second. New Jersey: Wiley. 2014: 349–360. ISBN 978-1848216402
Bachman, George; Narici, Lawrence; Beckenstein, Edward, Fourier and wavelet analysis, Universitext, Berlin, New York: Springer-Verlag , 2000, ISBN 978-0-387-98899-3MR 1729490 .Bers, Lipman ; John, Fritz ; Schechter, Martin, Partial differential equations, American Mathematical Society, 1981, ISBN 978-0-8218-0049-2Bourbaki, Nicolas , Spectral theories, Elements of mathematics, Berlin: Springer-Verlag, 1986, ISBN 978-0-201-00767-1Bourbaki, Nicolas , Topological vector spaces, Elements of mathematics, Berlin: Springer-Verlag, 1987, ISBN 978-3-540-13627-9Boyer, Carl Benjamin ; Merzbach, Uta C , A History of Mathematics 2nd, John Wiley & Sons, Inc., 1991, ISBN 978-0-471-54397-8Brenner, S.; Scott, R. L., The Mathematical Theory of Finite Element Methods 2nd, Springer, 2005, ISBN 978-0-387-95451-6 .Buttazzo, Giuseppe; Giaquinta, Mariano; Hildebrandt, Stefan, One-dimensional variational problems, Oxford Lecture Series in Mathematics and its Applications 15 , The Clarendon Press Oxford University Press, 1998, ISBN 978-0-19-850465-8MR 1694383 .Clarkson, J. A., Uniformly convex spaces, Trans. Amer. Math. Soc., 1936, 40 (3): 396–414, JSTOR 1989630 doi:10.2307/1989630 .Courant, Richard ; Hilbert, David , Methods of Mathematical Physics, Vol. I, Interscience, 1953Dieudonné, Jean , Foundations of Modern Analysis, Academic Press, 1960Dirac, P.A.M. , The Principles of Quantum Mechanics , Oxford: Clarendon Press, 1930Dunford, N.; Schwartz, J.T. , Linear operators, Parts I and II, Wiley-Interscience, 1958 .Duren, P., Theory of Hp -Spaces, New York: Academic Press, 1970 .Folland, Gerald B., Fourier analysis and its application Reprint of Wadsworth and Brooks/Cole 1992, American Mathematical Society Bookstore, 2009, ISBN 978-0-8218-4790-9 .Folland, Gerald B., Harmonic analysis in phase space, Annals of Mathematics Studies 122 , Princeton University Press, 1989, ISBN 978-0-691-08527-2 .Fréchet, Maurice, Sur les ensembles de fonctions et les opérations linéaires, C. R. Acad. Sci. Paris, 1907, 144 : 1414–1416 .Fréchet, Maurice, Sur les opérations linéaires, Transactions of the American Mathematical Society, 1904, 5 (4): 493–499, JSTOR 1986278 doi:10.2307/1986278 .Giusti, Enrico, Direct Methods in the Calculus of Variations, World Scientific, 2003, ISBN 978-981-238-043-2 .Grattan-Guinness, Ivor, The search for mathematical roots, 1870–1940, Princeton Paperbacks, Princeton University Press , 2000, ISBN 978-0-691-05858-0MR 1807717 .Halmos, Paul , Introduction to Hilbert Space and the Theory of Spectral Multiplicity, Chelsea Pub. Co, 1957Halmos, Paul , A Hilbert Space Problem Book, Springer-Verlag, 1982, ISBN 978-0-387-90685-0Hewitt, Edwin; Stromberg, Karl, Real and Abstract Analysis, New York: Springer-Verlag, 1965 .Hilbert, David ; Nordheim, Lothar Wolfgang ; von Neumann, John , Über die Grundlagen der Quantenmechanik, Mathematische Annalen, 1927, 98 : 1–30, S2CID 120986758 doi:10.1007/BF01451579 Holevo, Alexander S. , Statistical Structure of Quantum Theory, Lecture Notes in Physics, Springer, 2001, ISBN 3-540-42082-7OCLC 318268606 Kac, Mark , Can one hear the shape of a drum?, American Mathematical Monthly , 1966, 73 (4, part 2): 1–23, JSTOR 2313748 doi:10.2307/2313748 Kadison, Richard V.; Ringrose, John R., Fundamentals of the theory of operator algebras. Vol. I, Graduate Studies in Mathematics 15 , Providence, R.I.: American Mathematical Society , 1997, ISBN 978-0-8218-0819-1MR 1468229 .Kadison, Richard V.; Ringrose, John R., Fundamentals of the Theory of Operator Algebras, Vol. I: Elementary Theory, New York: Academic Press, Inc., 1983 Kakutani, Shizuo , Some characterizations of Euclidean space, Japanese Journal of Mathematics, 1939, 16 : 93–97, MR 0000895 doi:10.4099/jjm1924.16.0_93 Kline, Morris , Mathematical thought from ancient to modern times, Volume 3 3rd, Oxford University Press , 19721990, ISBN 978-0-19-506137-6Kolmogorov, Andrey ; Fomin, Sergei V. , Introductory Real Analysis Revised English edition, trans. by Richard A. Silverman (1975), Dover Press, 1970, ISBN 978-0-486-61226-3Krantz, Steven G. , Function Theory of Several Complex Variables, Providence, R.I.: American Mathematical Society , 2002, ISBN 978-0-8218-2724-6Lanczos, Cornelius, Applied analysis Reprint of 1956 Prentice-Hall, Dover Publications, 1988, ISBN 978-0-486-65656-4 .Lebesgue, Henri, Leçons sur l'intégration et la recherche des fonctions primitives , Gauthier-Villars, 1904 .Levitan, B.M., Hilbert space , Hazewinkel, Michiel (编), 数学百科全书 , Springer , 2001, ISBN 978-1-55608-010-4 .Lindenstrauss, J.; Tzafriri, L., On the complemented subspaces problem, Israel Journal of Mathematics , 1971, 9 (2): 263–269, ISSN 0021-2172 MR 0276734 S2CID 119575718 doi:10.1007/BF02771592 .Marsden, Jerrold E. , Elementary classical analysis, W. H. Freeman and Co., 1974, MR 0357693 Murphy, Gerald J., C*-algebras and Operator Theory, Academic Press, 1990, ISBN 0-12-511360-9 .von Neumann, John , Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren, Mathematische Annalen, 1929, 102 : 49–131, S2CID 121249803 doi:10.1007/BF01782338 Template:Narici Beckenstein Topological Vector Spaces von Neumann, John , Physical Applications of the Ergodic Hypothesis , Proc Natl Acad Sci USA, 1932, 18 (3): 263–266, Bibcode:1932PNAS...18..263N JSTOR 86260 PMC 1076204 PMID 16587674 doi:10.1073/pnas.18.3.263 von Neumann, John , Mathematical Foundations of Quantum Mechanics , Princeton Landmarks in Mathematics, 由Beyer, Robert T.翻译, Princeton University Press , 19551996, ISBN 978-0-691-02893-4MR 1435976 Nielsen, Michael A. ; Chuang, Isaac L. , Quantum Computation and Quantum Information 1st, Cambridge: Cambridge University Press , 2000, ISBN 978-0-521-63503-5OCLC 634735192 约翰·J·奥康纳; 埃德蒙·F·罗伯逊 , Abstract linear spaces , MacTutor数学史档案 , 1996 (英语) Peres, Asher , Quantum Theory: Concepts and Methods , Kluwer, 1993, ISBN 0-7923-2549-4OCLC 28854083 Prugovečki, Eduard, Quantum mechanics in Hilbert space 2nd, Dover, 19812006, ISBN 978-0-486-45327-9 .Reed, Michael ; Simon, Barry , Functional Analysis (vol I of 4 vols), Methods of Modern Mathematical Physics, Academic Press, 1980, ISBN 978-0-12-585050-6Reed, Michael ; Simon, Barry , Fourier Analysis, Self-Adjointness (vol II of 4 vols), Methods of Modern Mathematical Physics, Academic Press, 1975, ISBN 9780125850025Rieffel, Eleanor G. ; Polak, Wolfgang H., Quantum Computing: A Gentle Introduction , MIT Press, 2011-03-04, ISBN 978-0-262-01506-6(英语) Riesz, Frigyes , Sur une espèce de Géométrie analytique des systèmes de fonctions sommables, C. R. Acad. Sci. Paris, 1907, 144 : 1409–1411Riesz, Frigyes , Zur Theorie des Hilbertschen Raumes, Acta Sci. Math. Szeged, 1934, 7 : 34–38Riesz, Frigyes ; Sz.-Nagy, Béla , Functional analysis, Dover, 1990, ISBN 978-0-486-66289-3Template:Rudin Walter Functional Analysis Rudin, Walter , Real and Complex Analysis, McGraw-Hill, 1987, ISBN 978-0-07-100276-9Saks, Stanisław , Theory of the integral 2nd Dover, Dover, 2005, ISBN 978-0-486-44648-6Monografje Matematyczne , vol. 7, Warszawa, 1937.Template:Schaefer Wolff Topological Vector Spaces Schmidt, Erhard , Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten, Rend. Circ. Mat. Palermo, 1908, 25 : 63–77, S2CID 120666844 doi:10.1007/BF03029116 Shubin, M. A., Pseudodifferential operators and spectral theory, Springer Series in Soviet Mathematics, Berlin, New York: Springer-Verlag , 1987, ISBN 978-3-540-13621-7MR 0883081 .Sobrino, Luis, Elements of non-relativistic quantum mechanics, River Edge, New Jersey: World Scientific Publishing Co. Inc., 1996, Bibcode:1996lnrq.book.....S ISBN 978-981-02-2386-1MR 1626401 doi:10.1142/2865 .Stewart, James, Calculus: Concepts and Contexts 3rd, Thomson/Brooks/Cole, 2006 .Stein, E, Singular Integrals and Differentiability Properties of Functions ISBN 978-0-691-08079-6 .Stein, Elias ; Weiss, Guido , Introduction to Fourier Analysis on Euclidean Spaces ISBN 978-0-691-08078-9Streater, Ray ; Wightman, Arthur , PCT, Spin and Statistics and All That, W. A. Benjamin, Inc, 1964Teschl, Gerald . Mathematical Methods in Quantum Mechanics; With Applications to Schrödinger Operators . Providence : American Mathematical Society . 2009 [2022-09-19 ] . ISBN 978-0-8218-4660-5存档 于2022-08-12).Titchmarsh, Edward Charles , Eigenfunction expansions, part 1, Oxford University: Clarendon Press, 1946Trèves, François, Topological Vector Spaces, Distributions and Kernels, Academic Press, 1967 .Warner, Frank, Foundations of Differentiable Manifolds and Lie Groups, Berlin, New York: Springer-Verlag , 1983, ISBN 978-0-387-90894-6 .Weidmann, Joachim, Linear operators in Hilbert spaces, Graduate Texts in Mathematics 68 , Berlin, New York: Springer-Verlag , 1980, ISBN 978-0-387-90427-6MR 0566954 .Weyl, Hermann , The Theory of Groups and Quantum Mechanics English 1950, Dover Press, 1931, ISBN 978-0-486-60269-1Young, Nicholas, An introduction to Hilbert space, Cambridge University Press, 1988, ISBN 978-0-521-33071-8Zbl 0645.46024 .Jean Dieudonné, Foundations of Modern Analysis , Academic Press, 1960.
B.M. Levitan, Hilbert space , Hazewinkel, Michiel (编), 数学百科全书 , Springer , 2001, ISBN 978-1-55608-010-4