Prisekanost (geometrija)

Prisekanost je v geometriji operacija, ki v poljubni razsežnosti odreže politopu oglišča in pri tem tvori novo faceto povsod tam, kjer je prej bilo oglišče. Prisekanost (oznaka t_0,1) deluje na mnogokotnike in višjerazsežna telesa. Pri prisekanju se odrežejo oglišča in vstavi nova faceta tam, kjer je prej bilo oglišče. Stranske ploskve se prisekajo tako, da se pri tem podvojijo robovi.

Prisekana kocka ima dvojne stranske ploskve, oglišča zamenjana z novimi stranskimi ploskvami.

Uniformna prisekanost

V splošnem lahko prisekamo vsak polieder ali politop. Pri tem pa lahko izbiramo globino prisekanega (odsekanega) dela. To se vidi v Conwayjevi notaciji za prisekanost.

Posebna oblika prisekanosti je uniformna prisekanost, kjer operacijo prisekanosti uporabimo na pravilnih poliedrih ali pravilnih politopih. To kreira uniformne poliedre in uniformne politope z enakimi dolžinami robov.

Prisekani mnogokotniki

Prisekani mnogokotnik z n stranskimi ploskvami ima 2n stranskih ploskev (robov)

Prisekani pravilni poliedri in tlakovanje

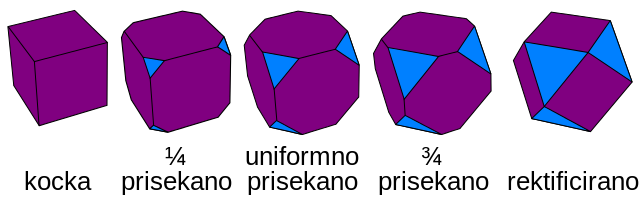
Naslednja slika prikazuje različne stopnje Prisekovanja vse od kocke do rektificirane kocke. Končna oblika poliedra je kubooktaeder. Srednja slika predstavlja uniformno prisekano kocko, ki ima Schläflijev simbol t_0,1{4,3}.

Ostale vrste prisekanj

V kvazipravilnih poliedrih je prisekovanje popolnejši izraz, kjer moramo izvesti še dodatne popravke, da bi prisekane stranske ploskve postale pravilne. To včasih imenujemo romboprisekanost.

Kot zgled poglejmo prisekani kubooktaeder, ki v resnici ni posledica prisekanosti, ker sekanje oglišč kubooktaedra da pravokotnike kot stranske ploskve in ne kvadratov. Potrebni so še nadaljnji postopki, da dobi polieder na stranskih ploskvah kvadrate.

Uniformni polieder in zgledi tlakovanja

Družina	Izvorno telo	Prisekano	Rektificirano	Dvojna prisekanost (prisekani dual)	Dvojna rektifikacija (dual)
[3,3]	Tetraeder	Prisekani tetraeder	Oktaeder	Prisekani tetraeder	Tetraeder
[4,3]	Kocka	Prisekana kocka	Kubooktaeder	Prisekani oktaeder	Oktaeder
[5,3]	Dodekaeder	Prisekani dodekaeder	Ikozidodekaeder	Prisekani ikozaeder	Ikozaeder
[6,3]	Šestkotno tlakovanje	Prisekano šestkotno tlakovanje	Trišestkotno tlakovanje	Šestkotno tlakovanje	Trikotno tlakovanje
[7,3]	Sedemkotno tlakovanje reda 3	Prisekano sedemkotno tlakovanje reda 3	Trisedemkotno tlakovanje	Prisekano trikotno tlakovanje reda 7	Trikotno tlakovanje reda 7
[8,3]	Osemkotno tlakovanje reda 3	Prisekano sedemkotno tlakovanje reda 3	Triosemkotno tlakovanje	Prisekano trikotno tlakovanje reda 8	Trikotno tlakovanje reda 8
[4,4]	Kvadratno tlakovanje	Prisekano kvadratno tlakovanje	Kvadratno tlakovanje	Prisekano kvadratno tlakovanje	Kvadratno tlakovanje
[5,4]	Pentagonalno tlakovanje	Prisekano pentagonalno tlakovanje	Rektificirano pentagonalno tlakovanje	Prisekano kvadratno tlakovanje	Kvadratno tlakovanje
[5,5]	Pentagonalno tlakovanje	Prisekano pentagonalno tlakovanje	Rektificirano pentagonalno tlakovanje	Prisekano pentagonalno tlakovanje	Pentagonalno tlakovanje

Zgledi prizmatičnih poliedrov

Družina	Izvorno telo	Prisekanost	Rektifikacija (tudi dual)
[2,p]	šestkotni hozoeder (kot sferno tlakovanje) {2,p}	šestkotna prizma t{2,p}	šestkotni dieder (kot sferno tlakovanje) {p,2}

Zgledi prisekanih rombov

Izvorno telo	Rektifikacija	Romboprisekanost
		Prisekani oktaeder
	Kubooktaeder	Prisekani kubooktaeder
	Ikozidodekaeder	Prisekani ikozidodekaeder
	Trišestkoto tlakovanje	Prisekano trikotno tlakovanje ali Veliko rombotrišesterokotno tlakovanje
	Trisedemkotno tlakovanje	Prisekano trisedemkotno tlakovanje ali Veliko rombotrisedemkotno tlakovanje
	Triosemkotno tlakovanje	Prisekano triosemkotno tlakovanje ali veliko rombotriosemkotno tlakovanje
	Kvadratno tlakovanje	Prisekano kvadratno tlakovanje
	Štiripetkotno tlakovanje	Prisekano štiripetkotno tlakovanje
	Petkotno tlakovanje reda 4	Prisekano petkotno tlakovanje reda 4

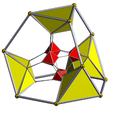
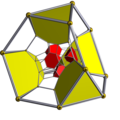
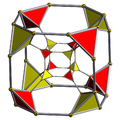
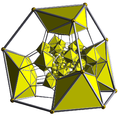
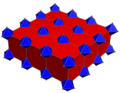
Prisekanost v polihorih in teselacijah satovja

Pravilni polihoroni ali prisekane teselacije {p, q, r} uniformni polihoroni ali teselacije z dvema celicama. Prisekane celice {p, q} in {q, r} nastanejo na prisekanem delu.

Družina [p,q,r]	Osnovna oblika	Prisekanost	Rektifikacija (Dvojno rektificirani duali)	Dvojna prisekanost (dvojno prisekani duali)
[3,3,3]	5-celica (sebi dualna)	Prisekana 5-celica	Rektificirana 5-celica	Dvojno prisekana 5-celica
[3,3,4]	16-celica	Prisekana 16-celica	rektificirana 16-celica (isto kot 24-celica)	Dvojno prisekana 16-celica (Dvojno prisekan teserakt)
[4,3,3]	Teserakt	Prisekani teserakt	Rektificirani teserakt	dvojno prisekan teserakt (Dvojno prisekana 16-celica)
[3,4,3]	24-celica (sebi dualna)	Prisekana 24-celica	Rektificirana 24-celica	Dvojno prisekana 24-celica
[3,3,5]	600-celica	Prisekana 600-celica	Rektificirana 600-celica	Dvojno prisekana 600-celica (Dvojno prisekana 120-celica)
[5,3,3]	120-celica	Prisekana 120-celica	Rektificirana 120-celica
[4,3,4]	kubično satovje (sebi dualno)	Prisekano kubično satovje	Rektificirano kubično satovje	Dvojno prisekano kubično satovje
[3,5,3]	Ikozaedersko satovje (sebi dualno)	(ni slike) Prisekano ikozaedersko satovje	(ni slike) Rektificirano ikozaedersko satovje reda 3	(ni slike) Dvojno prisekano ikozaedersko satovje reda 3
[4,3,5]	Kubično satovje reda 5	(ni slike) Prisekano kubično satovje reda 5	(ni slike) Rectificirano kubično satovje reda 5	(ni slike) Dvojno prisekano kubično satovje reda 5
[5,3,4]	Dodekaedersko satovje reda 4	(ni slike) Prisekano dodekaedersko satovje	(ni slike) Rektifificirano dodekaedersko satovje reda 4
[5,3,5]	(ni slike) Dodekaedersko satovje reda 5 (sebi dualno)	(ni slike) Prisekano dodekaedersko satovje reda 5	(ni slike) Rektificirano dodekaedersko satovje reda 5	(ni slike) Dvojno prisekano dodekaedersko satovje reda 5

Glej tudi

• uniformni polieder
• uniformni polihoron
• dvojna prisekanost (geometrija)
• rektifikacija (geometrija)

Zunanje povezave

• Prisekanost na MathWorld (angleško)
• Prisekanost v Glossary for Hyperspace (angleško)
• Imenovanje poliedrov (angleško)