From Wikipedia, the free encyclopedia
අවකාශය (ඉංග්රීසි: Space) යනු ස්ථාන සහ දිශා අඩංගු ත්රිමාන සන්තතිකයක් වේ.[1]
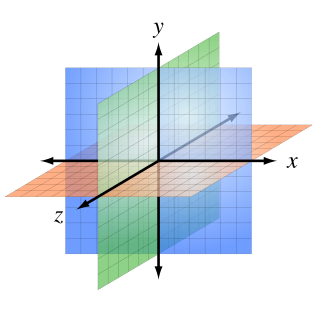
කාලය හා අවකාශය සත්ය ලෙසින්ම පවතින යථාර්ථයන් බවත්, වස්තූන් (Objects) අවකාශයෙහි ගිලි ඇති බවත්, සිද්ධීන් (Events) කාලයෙහි සිදුවන බවත් අයිසැක් නිවුටන් උපකල්පනය කළේය. වෙනත් ආකාරයකින් ප්රකාශ කරන්නේ නම් වස්තූන් අවකාශයෙන් වෙන්වන අතර සිද්ධීන් කාලයෙන් වෙන්වේ. යථාර්ථයක් වු අවකාශය, දිග, පළල හා උස යන ත්රිමානයන්ගෙන් සමන්විත බවත්, කාලය යන්න අවකාශයෙන් ස්වායත්ත වුවක් බවත්, කාලය රේඛීයව ඉදිරියට ගලා යන බවත් අයිසැක් නිවුටන් විශ්වාස කළේය. ලයිබ්නිස්ට (Leibniz)අනුව කාලය හා අවකාශය යනු පිළිවෙලින් සිද්ධීන් අතර හා වස්තූන් අතර සම්බන්ධය දැක්වීම සඳහා අප විසින් නිර්මාණය කරන ලද මනසේ කල්පිතයන් මිස යථාර්ථයන් නොවේ. ඔහුට අනුව සිද්ධීන් නැති අවස්ථාවකදී කාලය නොපවතී. එමෙන්ම වස්තූන් නැති තැන අවකාශයක්ද නැත. නිව්ටන් විසින් කරන ලද උපකල්පනයන් සාමාන්ය මනුෂ්යාගේ සංවේදනයන්, සංජානනයන් හා සමපාත වේ. සාමාන්ය මනුෂ්යයාට වැටහෙන පරිදි අවකාශය දිග, පළල හා උස යන ත්රිමානයන්ගෙන් යුක්තය. අවකාශයෙහි දිග, පළල, උස අපට අත්දැකීමෙන් හෝ මනසින් අවබෝධ කරගත හැකිය. එම මානයන්වලින් පෙන්වන දිශාවන්ට අපට චලනය විය හැකිය. අපට දැනෙන පරිදි අවකාශයට පරිබාහිරව කාලය පවතී. අපට දැනෙන පරිදි දිනක් අවෑමෙන් තව දිනක් උදා වේ. ඒ කාලය ගත වන බැවිණි. අපට කාලය ගලා යාමක් පිළිබඳ අදහසක් ඇත. අතීතයක්, වර්තමානයක්, අනාගතයක් ගැන අපි සංවේදී වෙමු. අපට දැනෙන පරිදි කාලය හා අවකාශය පවතින්නක් හෙවත් යථාර්ථයකි.
ස්වභාවදර්මය පිලිබද තිබෙන මතිමතාන්තර, එහි හරය සහ පවතින ලබන මාධ්යය පිළිබඳ ඇතිවූ මතගැටුම් ගල්යුගය දක්වා දිවයයි. උදාහරණ ලෙස ප්ලේටෝ (Plato) විසින් රචිත ටිමේයස් (Timaeus) ග්රන්ථය හදුන්වාදිය හැකිය.
ගැලීලියන් සහ කාටේසියන් විසින් අභ්යාවකාශය, අංශු සහ චලනය පිළිබද ඉදිරිපත් කරනු ලැබූ න්යායයන්, විද්යාත්මක විප්ලවයක් සඳහා මූලික අඩිතාලම සකසා දෙනු ලැබූ අතර එම න්යායයන්, නිව්ටන් විසින් 1687 දී ප්රකාශනය කරන ලද ප්රින්සිපියා මැතමැටිකා (Principia Mathematica) කෘතිය නිවැරදිව වටහා ගැනීමටද බොහෝ සෙයින් ඉවහල් වේ. ගැලීලියන්ගේ අවකාශය සහ කාල න්යායයන් අභ්යාවකාශ වස්තූන්ගේ චලනය පිළිබද විස්තර කරනු ලබයි. තවද මෙම න්යායයන්, භෟතික විද්යාව සඳහා විශාල බලපෑමක් සිදුකල අතර අභ්යාවකාශ ගවේශණයේ පුනරුදය මොහුගෙන් ආරම්භ වූ බව සලකනු ලබයි.
නුතන විද්යාවේ පුරෝගාමියෙකු වන ගැලීලියෝ විසින්, එවක පිලිගනු ලැබූ ඇරිස්ටෝල් (Aristotelian) සහ ප්ලේටෝ ( Ptolemaic) විසින් ඉදිරිපත් කල භූ කේන්ද්රීය කොස්මොස් (geocentric cosmos) න්යායය සංශෝධනය විය යුතු බව පෙන්වා දෙන ලදී. එමෙන්ම, ගැලීලියෝ විසින් නිකොලොස් කොපර්නිකස් Nicolaus Copernicus) විසින් ඉදිරිපත් කල සූර්ය කේන්ද්රීය (heliocentric) ආකෘතියේ නිරවද්යතාව පෙන්වා දෙන ලදී. මෙහිදී සූර්යයා මැදි කොට ගනිමින් අනෙකුත් ග්රහ වස්තූන් චලනය වන බව පිලිගනු ලබයි.
මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |

මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |


මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |

| Type of geometry | Number of parallels | Sum of angles in a triangle | Ratio of circumference to diameter of circle | Measure of curvature |
|---|---|---|---|---|
| Hyperbolic | Infinite | < 180° | > π | < 0 |
| Euclidean | 1 | 180° | π | 0 |
| Elliptical | 0 | > 180° | < π | > 0 |


මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |

මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
| සම්භාව්යය යාන්ත්ර විද්යාව | ||||||||||
නිව්ටන්ගේ දෙවැනි නියමය | ||||||||||
සම්භාව්යය යාන්ත්ර විද්යාවෙහි ඉතිහාසය · සම්භාව්යය යාන්ත්ර විද්යාවෙහි දින රේඛාව
| ||||||||||
මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
මෙම කොටස හිස්ය. එය පුළුල් කිරීමෙන් ඔබ හට උපකාර කළ හැක. |
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.