Paradoks bliźniąt

Paradoks bliźniąt, paradoks zegarów^[1] – eksperyment myślowy w szczególnej teorii względności, którego domniemana sprzeczność ma wykazywać nieprawdziwość tej teorii. Paradoks wynika z wyciągania wniosków z fałszywych założeń.

Jakościowa ilustracja paradoksu. Człowiek poruszający się nieinercjalnie – zaznaczony na czerwono – ulega dylatacji czasu.

Paradoks bliźniąt ma ogromne znaczenie dydaktyczne, gdyż jest bardzo często wykorzystywanym zagadnieniem, na przykładzie którego tłumaczone są konsekwencje szczególnej teorii względności, a dokładna analiza paradoksu pomogła zrozumieć tę teorię wielu pokoleniom uczniów.

Treść

Na Ziemi (lub w dowolnym punkcie wszechświata, przy założeniu, że z miejscem tym jest związany układ inercjalny) rodzą się bliźnięta. Jeden z nich pozostaje na Ziemi, a drugi, wysłany szybkim statkiem kosmicznym w przestrzeń kosmiczną, po pewnym czasie zawraca, ląduje na Ziemi i spotyka się ze swoim bratem bliźniakiem. Im statek będzie szybszy, tym spodziewany efekt będzie większy.

Zgodnie ze szczególną teorią względności czas w poruszającym się układzie odniesienia płynie wolniej (dylatacja czasu). Obserwacje bliźniaków przedstawiają się następująco:

1. Bliźniak pozostający na Ziemi spodziewa się, że skoro jego brat-kosmonauta poruszał się względem niego, to po powrocie brat-kosmonauta powinien być młodszy, jeśli dylatacja czasu jest prawdą.
2. Bliźniak-kosmonauta myśli, że w jego układzie odniesienia to właśnie brat pozostały na Ziemi poruszał się względem niego, a więc to na Ziemi czas powinien płynąć wolniej, czyli to bliźniak na Ziemi powinien być młodszy od bliźniaka-kosmonauty.

Jednak obaj bracia nie mogą mieć równocześnie racji.

Rozwiązanie

Błędne w powyższym rozumowaniu jest założenie czy przekonanie, że układy obu braci są równoważne. Tutaj tylko z jednym z nich można związać układ inercjalny. Gdyby obaj bracia mieli zawsze poruszać się względem siebie ze stałą prędkością, to nigdy, poza momentem wyruszania kosmonauty w podróż, nie spotkaliby się.

Paradoks ten wynika z niezrozumienia szczególnej teorii względności. Nie mówi ona bowiem, że wszyscy obserwatorzy są równoważni, a jedynie, że równoważni są obserwatorzy znajdujący się w układach inercjalnych, tzn. takich, które poruszają się względem siebie bez przyspieszenia. W tym przypadku brat-kosmonauta musi jednak zmienić swoją prędkość (czyli mieć pewne przyspieszenie), kiedy zawraca rakietę. Nie znajduje się on więc w tym samym układzie inercjalnym, co na początku. Rację ma więc jego brat, który pozostał na Ziemi.

Można rozpatrywać przykład z zegarami, aby efekty dylatacji były nie tylko subiektywne, ale i mierzalne. Niech każdy z braci ma swój zegar. Bracia zobowiązują się do wysyłania sygnałów „życzeń” co 1 rok według wskazań swoich zegarów, brat astronauta po przebyciu drogi 5 lat świetlnych zawraca i powraca na Ziemię^[2] .

Dla uproszczenia pominiemy problemy związane z rozpędzaniem, zawracaniem i zatrzymywaniem rakiety, przeciążeniami i wszystkie inne efekty^[2] .

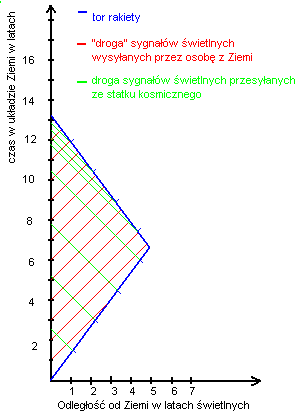
Sytuację przedstawia wykres (diagram Minkowskiego) położenie/czas w układzie odniesienia związanym z Ziemią. Sygnał „życzeń” biegnie z prędkością światła w próżni, dla czytelności dobieramy jednostki osi tak, by światło biegło pod kątem 45 stopni do osi układu współrzędnych; układ ten odpowiada latom na osi czasu i latom świetlnym na osi przestrzeni (położenia). Prędkość statku kosmicznego, wynoszącą około 0,745 prędkości światła w próżni, dobrano tak, by czynnik Lorentza^[2] :

${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {3}{2}}.}$

Wyjaśnienie ekspresowe: wystarczy policzyć (można na wykresie), ile życzeń wysłał każdy z braci, aby dowiedzieć się, ile lat im przybyło. I tak brat na Ziemi wysłał (czerwone linie) 13 komunikatów (ostatnia linia niewidoczna, odcinek bardzo krótki), przybyło mu więc ponad 13 lat, zaś brat w statku wysłał 8 (zielone linie), czyli przybyło mu ponad 8 lat (prawie 9). Zatem brat bliźniak na statku będzie o ponad 4 lata młodszy od brata, który nie podróżował^[2] .

Mechanika relatywistyczna i nierelatywistyczna

Mechanika nierelatywistyczna

W mechanice nierelatywistycznej czas jest niezależny od układu współrzędnych (czas absolutny) i zegary obu braci mają takie same wskazania.

Po roku brat z rakiety wysyła sygnał, ale jest już w odległości 0,75 roku świetlnego od Ziemi – i tyle (0,75 roku) światło będzie wracało. Pierwszy sygnał z rakiety dotrze więc na Ziemię 1,75 roku po starcie (1 rok podróży rakiety + 0,75 podróży powrotnej sygnału)^[2] .

W tym samym czasie (po roku) brat na Ziemi też wysyła sygnał. Sygnał ten „goni” statek kosmiczny z prędkością względną 1 − 0,75 = 0,25 prędkości światła w próżni, więc potrzebuje na dogonienie statku 3 lata, dotrze gdy na statku zegar będzie wskazywał 4 lata^[2] .

Widzimy brak symetrii choć nie ma powodu na wyróżnienie któregoś z braci (układu odniesienia), a obliczone czasy są sprzeczne. (Pokazują to także inne doświadczenia np. rozpadu poruszających się cząstek elementarnych). Wyróżnienie powstaje między innymi w wyniku tego, że prędkość światła w próżni uznajemy za jednakową względem Ziemi, ale wtedy w układzie statku musiałaby się zmieniać^[2] .

Mechanika relatywistyczna

Brat pozostający na Ziemi wysyła po roku sygnał, bieg sygnału ilustruje linia czerwona. Sygnał ten dociera do statku kosmicznego – zegar statku pokazuje wówczas 2,5 roku (widać na wykresie). Na Ziemi minęło 3,75 roku^[2] .

Brat w kosmosie wysyła życzenia, gdy minie u niego 1 rok (ale jest to wtedy, gdy na Ziemi minie 1,5 roku), a statek jego jest w odległości 1 roku świetlnego od Ziemi, więc sygnał dotrze do odbiorcy gdy na Ziemi będzie 2,5 roku (według obliczeń brata na statku jego brat na Ziemi otrzyma życzenia gdy zegar na statku pokazuje 3,75 roku)^[2] .

Zauważmy symetrię: obaj bracia wysyłają życzenia co rok, a otrzymują co 2,5 roku, każdy z nich może tłumaczyć, że ten drugi oddala się. I wszystko jest w porządku, układy poruszają się ze stałą prędkością (są inercjalne)^[2] .

Brat astronauta po 5 latach zawraca, w trakcie zawracania jest poddawany przyspieszeniu, a oznacza to, że w tym czasie nie jest w układzie inercjalnym. Po zawróceniu porusza się ze stałą prędkością, oznacza to że jest w układzie inercjalnym – ale nie w tym samym, w którym był podczas oddalania się od Ziemi^[2] .

Jaka jest różnica wieku braci? Jeżeli bratu na Ziemi przybyło ${\displaystyle t}$ lat, to bratu w kosmosie ${\displaystyle t/1{,}5,}$ czyli ${\displaystyle 2/3\cdot t.}$ Różnica wynosi ${\displaystyle (1-1/1{,}5)\cdot t,}$ czyli ${\displaystyle 1/3\cdot t}$^[2] .

Zobacz też

• synchronizacja zegarów

Przypisy

1. paradoks zegarów, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2021-10-02].
2. Wróblewski i Zakrzewski 1984 ↓.

Bibliografia

• Andrzej Kajetan Wróblewski, Janusz Andrzej Zakrzewski: Wstęp do fizyki. Warszawa: Państwowe Wydawnictwo Naukowe, 1984, s. 223–231. ISBN 83-01-01359-1.

Linki zewnętrzne

Nagrania na YouTube (ang.) [dostęp 2024-08-22]:

• Don Lincoln, Twin paradox: the real explanation, kanał Fermilabu, 13 marca 2018.
• Amber Stuver, Einstein's twin paradox explained, kanał TED-Ed, 26 września 2019.

Encyklopedie internetowe (paradoks):

• Britannica: science/twin-paradox
• БРЭ: 2706721
• SNL: tvillingparadokset
• Catalana: 0199055
• DSDE: tvilling-paradokset