상위 질문
타임라인
채팅
관점
콕서터 군
위키백과, 무료 백과사전
Remove ads
군론에서 콕서터 군(Coxeter群, 영어: Coxeter group)은 일련의 반사들로 구성되는 군이다. 단순 리 군의 바일 군은 유한 콕서터 군이며, 따라서 유한 콕서터 군은 단순 리 군과 유사하게 분류할 수 있다. 또한, 다각형이나 다면체의 반사 대칭군 또한 유한 콕서터 군이므로, 콕서터 군은 정다면체의 분류와도 관련있다.
정의
요약
관점
여기서 행렬 는 다음과 같은 성질들을 만족시킨다.
- (). 여기서 인 경우는 의 꼴의 관계를 아예 적용하지 않아야 한다는 뜻이다.
이 행렬 을 콕서터 군의 콕서터 행렬(Coxeter行列, 영어: Coxeter matrix)이라고 하고, 을 콕서터 군의 계수(階數, 영어: rank)라고 한다. 순서쌍 을 콕서터 계(Coxeter系, 영어: Coxeter system)라고 한다. 두 콕서터 군이 군으로서 동형이더라도, 서로 동형이 아닌 콕서터 계를 가질 수 있다. 예를 들어, 군으로서 이지만, 이들은 서로 다른 콕서터 계를 가진다. 그러나 콕서터 군의 계수는 표시에 관계없는 불변량이다.
콕서터 행렬 · 슐레플리 행렬 · 콕서터 도표
콕서터 군의 콕서터 행렬 은 다른 방법으로 표기할 수 있다.
콕서터 도표(Coxeter圖表, 영어: Coxeter diagram)은 콕서터 군을 그래프로 나타내는 방법이다. 구체적으로, 이는 각 변에 유리수 가 붙은 그래프이다.
- 콕서터 도표의 각 꼭짓점은 어떤 거울 반사의 반사면을 나타낸다.
- 콕서터 도표의 두 꼭짓점 사이의, 수 가 붙은 변은 두 거울 반사 사이의 각도가 라는 것을 뜻한다. 그림을 간략하게 하기 위하여, 통상적으로 다음과 같은 규칙을 따른다.
- 인 경우, 즉 두 변 사이에 각도가 인 경우에는 변을 통상적으로 생략한다.
- 인 경우, 즉 두 변 사이에 각도가 인 경우에는 변을 그리되, 를 통상적으로 생략한다.
- 인 경우 통상적으로 변 및 의 값을 생략하지 않는다.
콕서터 행렬 에 대응하는 슐레플리 행렬(영어: Schläfli matrix) 의 성분은 다음과 같다.
즉, 콕서터 행렬은 두 반사면 사이의 각도의 라디안 값 의 분모 를 나타내는 반면, 슐레플리레 행렬은 각도의 코사인의 −2배를 표기한다.
예를 들어, 비교적 간단한 콕서터 군들의 콕서터 행렬 · 슐레플리 행렬 · 콕서터 도표는 다음과 같다.
콕서터 군은 그 슐레플리 행렬 의 고윳값들에 따라서 다음과 같이 세 종류로 분류된다.
- 유한 콕서터 군(영어: finite Coxeter group): 의 고윳값들이 모두 양의 실수이다. 이 경우는 유한군이며, 폴리토프(=초구의 테셀레이션)의 대칭군과 관련있다.
- 아핀 콕서터 군(영어: affine Coxeter group): 의 고윳값들이 모두 음의 실수가 아니며, 0을 고윳값으로 갖는다. 이 경우는 무한군이며, 유클리드 공간의 테셀레이션의 대칭군과 관련있다.
- 쌍곡선 콕서터 군(영어: hyperbolic Coxeter group): 는 하나 이상의 음의 고윳값을 갖는다. 이 경우는 무한군이며, 쌍곡공간의 테셀레이션의 대칭군과 관련있다.
Remove ads
성질
크기
유한 콕서터 군의 크기 는 그 콕서터 수 와 다음과 같이 관계있다.[1]:233
- [p]: 2h/gp = 1
- [p,q]: 8/gp,q = 2/p + 2/q -1
- [p,q,r]: 64h/gp,q,r = 12 - p - 2q - r + 4/p + 4/r
- [p,q,r,s]: 16/gp,q,r,s = 8/gp,q,r + 8/gq,r,s + 2/(ps) - 1/p - 1/q - 1/r - 1/s +1
호몰로지
콕서터 군은 유한 개의, 차수 2의 원소들로 생성되었으므로, 그 아벨화(=1차 군 호몰로지)는 2차 순환군 들의 유한 개의 직합이다. 콕서터 군의 슈어 승수(=2차 군 호몰로지) 역시 알려져 있다.[2][3][4]
불변량
계수 의 유한 콕서터 군 는 차원 (실수) 벡터 공간 위에 자연스러운 표현을 갖는다. 이 경우, 의 작용에 대하여 불변인 다항식들의 대수 을 생각할 수 있다.
이는 항상 자유 가환 단위 결합 대수(=다항식 대수)를 이룬다. 불변량 대수 의 생성원들의 수는 군의 계수 이며, 불변량 대수의 생성원(기본 불변량 영어: fundamental invariant)들의 차수는 아래 표에 제시하였다. 이들은 다음과 같은 성질을 보인다.
- 생성원들의 차수 가운데 최댓값은 항상 콕서터 수 이며, 최솟값은 2이다.
- 차수 의 생성원이 존재한다면, 차수 의 생성원 역시 존재한다.
콕서터 원소
반사 으로 생성되는 콕서터 군 의 콕서터 원소는 다음과 같은 꼴의 원소이다.
물론, 이는 순열 에 의존하며, 일반적으로 유일하지 않으나, 모든 콕서터 원소는 하나의 켤레류에 속한다. 특히, 모든 콕서터 원소는 같은 차수를 갖는다. 콕서터 원소의 차수를 콕서터 군 의 콕서터 수(Coxeter數, 영어: Coxeter number)라고 한다.
길이 함수
콕서터 군 위에는 다음과 같은 콕서터 길이 함수가 존재한다.
이는 원소를 나타내기 위하여 필요한 반사의 수이다. 이 길이 함수를 사용하여 위에 여려 부분 순서를 정의할 수 있으며, 또한 유한 콕서터 군의 경우 유일한 최장(最長) 원소가 존재한다.
Remove ads
분류
요약
관점
유한 콕서터 군
유한 콕서터 군들은 모두 완전히 분류되었고, 다음 표와 같다. 두 유한 콕서터 군의 곱은 또다른 유한 콕서터 군이므로, 아래 표는 두 콕서터 군의 곱으로 나타낼 수 없는 콕서터 군들만을 나열하였다. 유한 콕서터 군의 기호에서 아랫첨자는 콕서터 군의 계수(즉, 콕서터 도표의 점의 수)와 같다.
위 목록에서, 다음과 같은 항목들이 서로 중복된다.
또한, 및 을 작은 에 대하여 그대로 연장한다면 다음과 같은 항목들이 중복된다.
바일 군은 유한 콕서터 군 가운데, 결정 조건(結晶條件, 영어: crystallographic condition)을 만족시키는 것이다. 여기서 결정 조건이란 콕서터 도표의 모든 변에 대하여, 첨부된 숫자가 2, 3, 4, 또는 6 (즉, 90°, 60°, 45°, 30°)이어야 한다는 것이다. 이 경우, 또는 인 경우는 각각 딘킨 도표에서 변이 2겹 또는 3겹인 경우에 해당한다. 따라서, 유한 콕서터 군 가운데 바일 군인 것들은 다음 목록에 수록된 군들의 직접곱이다.
- . 이들은 리 군 및 의 바일 군이다.
- , ,
- . 이는 의 바일 군이다.
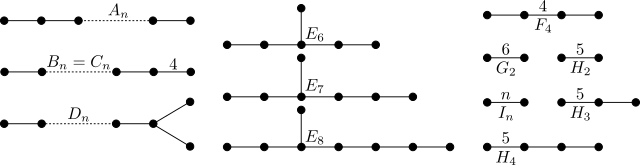
유한 콕서터 군들의 콕서터 도표는 다음과 같다.
아핀 콕서터 군
아핀 콕서터 군의 기호의 아랫첨자는 계수(콕서터 도표의 꼭짓점의 수)보다 1 작으며, 이들은 대응하는 유한 콕서터 군의 기호에 물결표(~)를 덧씌워 표기한다.
아핀 콕서터 군의 콕서터 도표는 다음과 같다.
쌍곡선 콕서터 군
쌍곡선 콕서터 군(영어: hyperbolic Coxeter group)의 분류는 유한 콕서터 군이나 아핀 콕서터 군의 분류보다 더 복잡하다.
Remove ads
역사
해럴드 스콧 맥도널드 콕서터가 1930년대에 도입하였다.[5][6] 이후 자크 티츠와 니콜라 부르바키가 콕서터 군의 이론의 발전에 공헌하였다.
각주
같이 보기
외부 링크
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads





















 ,
,  ...
...























![{\displaystyle \mathbb {C} [V]^{G}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0b8aa84fe65eff92c22cbe13157edaa773ca6867)






 ,
,  ...
...




























 ,
,  ...
...
















