바이어슈트라스 함수

비슷한 이름의 바이어슈트라스 타원함수에 관해서는 해당 문서를 참고하십시오.

수학에서 바이어슈트라스 함수(-函數, 영어: Weierstrass function)는 칸토어 함수의 한 예이다. 모든 점에서 연속이나, 모든 점에서 미분 불능이다. 독일의 수학자 카를 바이어슈트라스가 제안하였다.

구간 ${\displaystyle [-2,2]}$ 위의 바이어슈트라스 함수의 그래프. 프랙탈로서 자기 유사성을 띤다, 즉 부분을 확대하면 (빨간 원) 자기 자신과 유사하다.

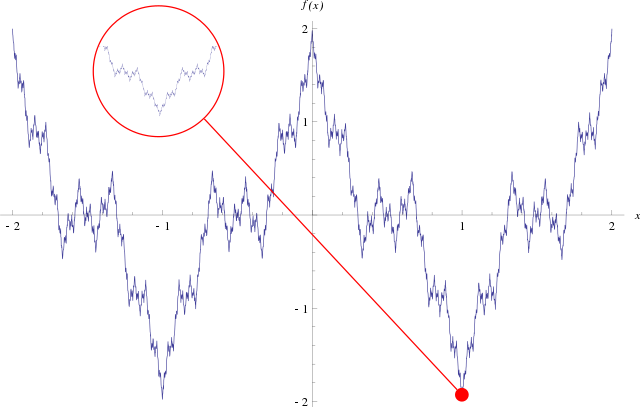
바이어슈트라스 함수는 '모든 연속함수는 많아 봐야 고립점들의 집합에서만 미분 불가능'이라는 생각의 처음 출간된 (1872) 반례이기에 역사적 중요성을 띤다.^[1]

정의

${\displaystyle a=0.5}$, ${\displaystyle b}$는 0.1부터 5까지 선형 증가.

아래는 바이어슈트라스의 논문 원본에서의 정의이다.

${\displaystyle f(x)=\sum _{n=0}^{\infty }a^{n}\cos(b^{n}\pi x)}$

(단, ${\displaystyle 0<a<1}$, ${\displaystyle b}$는 양의 홀수, ${\displaystyle ab>1+{\frac {3}{2}}\pi }$)

위 조건을 만족하는 ${\displaystyle b}$의 최솟값은 ${\displaystyle b=7}$이다. 이 함수의 정의와 모든 점에서의 미분 불가능성의 증명은 1872년 7월 18일 바이어슈트라스가 프로이센 과학 아카데미에 제출한 논문에서 처음 발표되었다.^[2][3][4]

실해석학에서 바이어슈트라스 함수는 흔히 그와 비슷한 정의와 성질을 가진 함수를 지칭하는 데 쓰인다. 그 예로 무한급수 안의 코사인 함수를 삼각파로 대신한 것이 있다.

${\displaystyle 0<a<1}$, ${\displaystyle ab\geq 1}$의 전제 하에 모든 점에서 미분 불능임을 고드프리 해럴드 하디가 증명하였다.^[5]

연속성과 미분가능성

바이어슈트라스 함수는 모든 점에서 연속이나, 모든 점에서 미분 불능이다.

모든 점에서의 연속성은 바이어슈트라스 M-판정법에서 ${\displaystyle M_{n}=a^{n}}$을 취하면 쉽게 증명된다.

모든 점에서의 미분 불가능성을 증명하려면, 임의의 ${\displaystyle x\in \mathbb {R} }$가 주어질 때, 두 수열 ${\displaystyle x_{n},x_{n}'}$을 구성하여 아래를 증명하면 된다.

${\displaystyle \liminf _{n\to \infty }{\frac {f(x_{n})-f(x)}{x_{n}-x}}>\limsup _{n\to \infty }{\frac {f(x_{n}')-f(x)}{x_{n}'-x}}}$

위에서 ${\displaystyle \liminf }$와 ${\displaystyle \limsup }$는 각각 하극한과 상극한이다.

모든 연속함수는 모든 점에서 미분 가능하거나 아주 작은 집합에서만 미분 불가능이라는 관념은 오래 존재해왔다. 바이어슈트라스의 논문에 의하면, 가우스를 비롯한 초기 수학자들은 이를 자주 기정 사실로 취급하였다. 반례를 찾아내기가 어려운 것이 이유일 수 있다. 실제로 일부 더 강한 조건의 연속성(예를 들어 립시츠 연속성)은 거의 어디서나 미분 가능임을 함의한다(레이드매처의 정리). 우리가 연속 함수를 그릴 때에도 결과물은 대개 립시츠 연속성 등의 더 좋은 성질을 가진다.

프랙탈

바이어슈트라스 함수는 최초의 프랙탈 중 하나로, 자기 유사성을 지닌다. 따라서 곡선을 확대해도 직선에 가까워지지 않으며 임의의 두 점 사이에서 단조성이 없다. 바이어슈트라스 함수의 하우스도르프 차원 ${\displaystyle D}$는 ${\displaystyle 2+{\frac {\ln a}{\ln b}}}$를 상계로 갖는다. 일반적으로 ${\displaystyle D=2+{\frac {\ln a}{\ln b}}}$라고 추측하나 아직 증명되지 않았다.^[6][7]

횔더 연속성

다음은 바이어슈트라스 함수의 동등한 표현이다.

${\displaystyle W_{\alpha }(x)=\sum _{n=0}^{\infty }b^{-n\alpha }\cos(b^{n}x)}$

이 중 ${\displaystyle \alpha }$는 ${\displaystyle 0<\alpha <1}$을 만족한다. ${\displaystyle W_{\alpha }(x)}$는 α-횔더 연속성을 가진다. 즉, 상수 ${\displaystyle C}$가 존재하여 임의의 ${\displaystyle x,y}$에 대하여^[8]

${\displaystyle |W_{\alpha }(x)-W_{\alpha }(y)|\leq C|x-y|^{\alpha }}$

더 나아가 ${\displaystyle W_{\alpha }(x)}$는 임의의 ${\displaystyle 0\leq \alpha <1}$에 대해 α-횔더 연속이지만 립시츠 연속(즉 1-횔더 연속)은 아니다.

모든 곳에서 미분 불능인 함수의 조밀성

바이어슈트라스 함수가 소수 특례인 것은 아니다. 병적이지만 연속함수에게는 일반적이라는 것이다.

• 위상수학의 관점에서, ${\displaystyle [0,1]}$ 위의 연속 실가 함수의 균등 수렴 위상을 가진 벡터 공간 ${\displaystyle C([0,1];\mathbb {R} )}$에서, ${\displaystyle [0,1]}$ 위의 온 곳에서 미분 불능인 함수의 집합은 나머지 집합을 이룬다.^[9][10]
• 측도론의 관점에서, 공간 ${\displaystyle C([0,1];\mathbb {R} )}$에 고전적 위너 측도 ${\displaystyle \gamma }$를 부여했을 때 적어도 한 점에서 미분 가능한 함수의 집합은 γ-영측도이다.

같이 보기

• 코크 곡선
• 블랑망제 곡선
• 바이어슈트라스 시그마 함수
• 바이어슈트라스 제타 함수