Valószínűségi mező

A valószínűségi mező a valószínűségszámítás egyik legfontosabb fogalma. Olyan folyamatokat (vagy „kísérleteket”) modellez, amelyeknek köze van a véletlenhez.

Definíció

A rövid definíció szerint a valószínűségi mező egy olyan mértéktér, ahol a teljes tér mértéke 1. Bővebben:

Legyen ${\displaystyle \Omega }$ tetszőleges halmaz. Ha a ${\displaystyle {\mathcal {P}}(\Omega )}$ hatványhalmaz egy ${\displaystyle {\mathcal {A}}}$ részhalmaza ${\displaystyle ({\mathcal {A}}\subseteq {\mathcal {P}}(\Omega ))}$ σ-algebra, azaz

• ${\displaystyle \emptyset \in {\mathcal {A}}}$, vagyis az üreshalmaz ${\displaystyle {\mathcal {A}}}$-beli,
• minden ${\displaystyle A\in {\mathcal {A}}}$ halmaz esetén ${\displaystyle \Omega \setminus A\in {\mathcal {A}}}$, vagyis az ${\displaystyle \Omega }$-ra vett komplementer halmaz is ${\displaystyle {\mathcal {A}}}$-beli, és
• minden ${\displaystyle (A_{n})\subseteq {\mathcal {A}}}$ halmazsorozat esetén ${\displaystyle \bigcup _{n=1}^{\infty }A_{n}\in {\mathcal {A}}}$,

és létezik egy ${\displaystyle P:{\mathcal {A}}\to [0,1]}$ mérték, hogy

• ${\displaystyle P(\emptyset )=0}$,
• ${\displaystyle P(\Omega )=1}$, és
• minden ${\displaystyle (A_{n})\subseteq {\mathcal {A}}}$ páronként diszjunkt halmazokból álló halmazsorozat esetén ${\displaystyle P\left(\bigcup _{n=1}^{\infty }A_{n}\right)=\sum _{n=1}^{\infty }P(A_{n})}$,

akkor az ${\displaystyle (\Omega ,{\mathcal {A}},P)}$ hármast valószínűségi mezőnek nevezzük.

Szerencsekerék modellezése valószínűségi mezővel: az összes lehetséges kimenetel itt ${\displaystyle \Omega =\{1,2,3\}}$. Az ${\displaystyle \Omega }$ alaphalmaz részhalmazainak valószínűségét szektora szögének a teljesszöghöz (360°) viszonyított nagysága adja meg

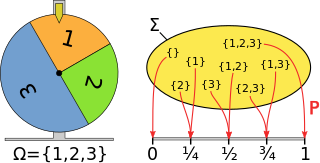
Ez a definíció azt is jelenti, hogy a valószínűség fogalma tisztán axiomatikus felírással is kezelhető, és nemcsak empirikusan – ahogy azt von Mises leírta. Alapvető az a gondolat, hogy a véletlen kísérlet összes kimenetét egymást kizáró eseményekként adjuk meg. Például egy szerencsekerék csak egy pozícióban állhat meg, ami egy adott null pozícióhoz képest mérhető. A mellékelt kép által mutatott példában csak az 1, 2, 3 számokhoz tartozó tartományokban állhat meg; egy mechanizmus akadályozza meg, hogy pont két szám határára essen (aminek egyébként is nulla a valószínűsége). Emiatt nem következhet be két elemi esemény, ezek diszjunktak. Ez alapozza meg az összeadási tétel kiterjesztését: Véges sok, egymást kölcsönösen kizáró esemény együttes valószínűsége az egyes események valószínűségeinek összege.

Elnevezések

• Az ${\displaystyle \Omega }$ halmaz eseménytér.

Az ${\displaystyle \omega \in \Omega }$ elemeket kimeneteleknek, vagy néha pongyolán elemi eseményeknek nevezzük; bár elemi eseménynek inkább az ezeket egyetlen elemként tartalmazó halmazokat célszerű nevezni, hiszen a ${\displaystyle P}$ mértékfüggvény halmazokon értelmezett, lásd alább.

• Az ${\displaystyle {\mathcal {A}}\subseteq {\mathcal {P}}(\Omega )}$ σ-algebra az eseményalgebra.

Az ${\displaystyle A\in {\mathcal {A}}}$ halmazok események.

Az egyetlen lehetséges kimenetelt tartalmazó ${\displaystyle A_{i}=\{\omega _{i}\}}$ halmazok az elemi események

• A ${\displaystyle P:{\mathcal {A}}\to [0,1]}$ mértékfüggvény a valószínűségi mérték, röviden a valószínűség.

Az ${\displaystyle \Omega \in {\mathcal {A}}}$ esemény biztos esemény, mert ${\displaystyle P(\Omega )=1}$.

Az ${\displaystyle \emptyset \in {\mathcal {A}}}$ esemény lehetetlen esemény, mert ${\displaystyle P(\emptyset )=0}$.

Az ${\displaystyle {\overline {A}}=\Omega \setminus A\in {\mathcal {A}}}$ esemény az ${\displaystyle A\in {\mathcal {A}}}$ esemény komplementere.

• Az ${\displaystyle (\Omega ,{\mathcal {A}},P)}$ hármast valószínűségi mezőnek vagy valószínűségi térnek nevezzük.

Példák

Példák diszkrét valószínűségi mezőre

Általánosabban, diszkrét valószínűségi mezőről van szó, ha az eseménytér véges vagy megszámlálhatóan végtelen, és eseményalgebrája a hatványhalmaz, vagyis ${\displaystyle {\mathcal {A}}={\mathcal {P}}(\Omega )}$. Ebben az esetben nincsen szükség a σ-algebra fogalmának bevezetésére, ${\displaystyle (\Omega ,P)}$ diszkrét valószínűségi mezőről beszélhetünk.^[1]

Klasszikus valószínűségi mező

Legyen ${\displaystyle \Omega }$ véges halmaz, ${\displaystyle {\mathcal {A}}={\mathcal {P}}(\Omega )}$ és minden ${\displaystyle A\in {\mathcal {P}}(\Omega )}$ halmaz esetén ${\displaystyle P(A)={\frac {|A|}{|\Omega |}}}$. Ekkor az ${\displaystyle (\Omega ,{\mathcal {P}}(\Omega ),P)}$ valószínűségi mezőt klasszikus valószínűségi mezőnek nevezzük.

Akkor is beszélnek diszkrét valószínűségi mezőről, ha az ${\displaystyle \Omega }$ eseménytér tetszőleges, de a valószínűségek mindig egy véges vagy megszámlálhatóan végtelen halmaz elemeit veszik fel, azaz ennek a halmaznak 1 a valószínűsége.^[2]

Bernoulli-mező

Ha az alaphalmaz, ${\displaystyle \Omega =\{0,1\}}$ a valószínűségek pedig ${\displaystyle P(\{0\})=p,P(\{1\})=1-p}$, akkor Bernoulli-mezőről van szó.^[3]

Poisson-eloszlásból származtatott

A természetes számok halmaza, mint eseménytér, azaz ${\displaystyle \mathbb {N} =\{0,1,2,\dots \}}$, minden természetes szám lehetséges kimenetel.

Az események ennek véges vagy megszámlálható végtelen részhalmazai.

Valószínűségi mérték lehet a ${\displaystyle P_{\lambda }}$ Poisson-eloszlás. A ${\displaystyle \{k\}}$ szám valószínűsége ${\displaystyle P_{\lambda }(k)={\frac {\lambda ^{k}}{k!}}\,\mathrm {e} ^{-\lambda }}$, ahol ${\displaystyle \lambda }$ pozitív paraméter.

Ezzel ${\displaystyle (\mathbb {N} ,{\mathcal {P}}(\mathbb {N} ),P_{\lambda })}$ diszkrét valószínűségi tér.

Példák nem diszkrét valószínűségi mezőre

Geometriai valószínűségi mező

Legyen ${\displaystyle \Omega \subset \mathbb {R} ^{n}}$ olyan Lebesgue mérhető halmaz, amelynek Lebesgue-mértéke ${\displaystyle \lambda (\Omega )}$ véges, ${\displaystyle {\mathcal {A}}={\mathcal {L}}(\Omega )}$ az ${\displaystyle \Omega }$ halmaz Lebesgue mérhető részhalmazainak ${\displaystyle \scriptstyle \sigma }$-algebrája és minden ${\displaystyle A\in {\mathcal {L}}(\Omega )}$ esemény esetén ${\displaystyle P(A)={\frac {\lambda (A)}{\lambda (\Omega )}}}$. Ekkor az ${\displaystyle (\Omega ,{\mathcal {L}}(\Omega ),P)}$ valószínűségi mezőt geometriai valószínűségi mezőnek nevezzük.

Exponenciális eloszlásból származtatott

Az eseménytér a nemnegatív számok ${\displaystyle \Omega =\mathbb {R} _{\geq 0}=[0,\infty )}$ halmaza.

Az események az ${\displaystyle \Omega =\mathbb {R} _{\geq 0}=[0,\infty )}$ Borel-részhalmazai, azaz ${\displaystyle {\mathcal {B}}(\mathbb {R} )\cap [0,\infty )={\mathcal {B}}([0,\infty ))}$. Ezzel minden nyílt, zárt, félig nyílt intervallum, ezek egyesítése, metszete és komplementere esemény.

Valószínűségi mérték lehet az exponenciális eloszlás, ami minden ${\displaystyle A}$ Borel-halmazhoz a

${\displaystyle P_{\mathrm {Exp} (\lambda )}(A)=\int _{A}\lambda \exp(-\lambda x)\mathrm {d} x}$

valószínűséget rendeli, ahol ${\displaystyle \lambda >0}$ paraméter.

Ezzel ${\displaystyle ([0,\infty ),{\mathcal {B}}([0,\infty )),P_{\mathrm {Exp} (\lambda )})}$ valószínűségi mező.

További példák

• Indukált valószínűségi mező, ami egy valószínűségi változó képtere, ellátva a valószínűségi változó eloszlásával mint valószínűséggel.
• Teljes valószínűségi mező, teljes mértéktér a valószínűséggel mint mértékkel.
• Szorzattér
• Szűrt valószínűségi mező, valószínűségi mező szűrővel.

Kapcsolódó szócikkek

• Valószínűségi változó

Jegyzetek

1. Ulrich Krengel. Einführung in die Wahrscheinlichkeitstheorie und Statistik. Für Studium, Berufspraxis und Lehramt, 8., Wiesbaden: Vieweg (2005). ISBN 3-8348-0063-5
2. David Meintrup, Stefan Schäffler. Stochastik. Theorie und Anwendungen. Berlin Heidelberg New York: Springer-Verlag (2005). ISBN 978-3-540-21676-6
3. Ehrhard Behrends. Elementare Stochastik. Ein Lernbuch – von Studierenden mitentwickelt. Wiesbaden: Springer Spektrum (2013). ISBN 978-3-8348-1939-0

Források

• V.V. Sazonov: Probability space
• Weisstein, Eric W.: Probability Space (angol nyelven). Wolfram MathWorld
• Hans-Otto Georgii. Stochastik. Einführung in die Wahrscheinlichkeitstheorie und Statistik, 4., Berlin: Walter de Gruyter (2009). ISBN 978-3-11-021526-7
• Norbert Henze. Stochastik für Einsteiger., 10., Wiesbaden: Springer Spektrum (2013, isbn=978-3-658-03076-6,)
• Achim Klenke. Wahrscheinlichkeitstheorie, 3., Berlin Heidelberg: Springer-Verlag (2013). ISBN 978-3-642-36017-6
• Klaus D. Schmidt. Maß und Wahrscheinlichkeit, 2., átnézett, Heidelberg Dordrecht London New York: Springer-Verlag (2011). ISBN 978-3-642-21025-9

Fordítás

Ez a szócikk részben vagy egészben a Wahrscheinlichkeitsraum című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.