Mesterséges neurális hálózat

A mesterséges neurális hálózat, mesterséges neuronháló vagy ANN (artificial neural network) biológiai ihletésű szimuláció. Fő alkalmazási területe a gépi tanulás, melynek célja ezeknek a hálóknak a tanuló rendszerként történő gyakorlati alkalmazása. Gráf alapú modell, melyben rétegekbe rendezett mesterséges neuronok kommunikálnak egymással nemlineáris aktivációs függvényeken keresztül. A legalább három rétegbe rendezett, nemlineáris aktivációs függvényt használó neurális hálózat univerzális függvényapproximátor,^[1] a visszacsatolásokat, rekurrenciát tartalmazó architektúrák pedig Turing-teljességgel rendelkeznek, így képesek megoldani bármilyen problémát vagy futtatni bármilyen algoritmust, amit számítógép segítségével meg lehet oldani vagy futtatni lehet.^[2]

Tanításuk általában a hiba-visszaterjesztéssel (backpropagation of errors) kombinált gradiensereszkedéssel történik, de számos alternatív algoritmus is elérhető ezeken kívül.

Történetük

A mesterséges neuron ma is használt modellje a Hebb tanulásban és a küszöblogikában gyökerezik, előbbi leírta, hogy a tanulás nem passzív folyamat, hanem az ideghálózatban ideiglenesen vagy véglegesen bekövetkező biokémiai és fiziológiai változások összessége, az úgynevezett neuroplaszticitás, mely szerint az együtt tüzelő neuronok egymás iránt fogékonyabbak, egymás jelére érzékenyebbek lesznek.^[3] A küszöblogika a neuron egyik első modellje, a neuront számítási egységként kezeli, melynek több bemenete és egy kimenete van (a biológiai neuron számos dendritjének és egyetlen axonjának analógiájára). A bemenetekhez egyedi súlyok tartoznak, melyekből lineáris kombinációval előállítható a neuron izgatottsága. Ha az izgatottság egy megadott küszöbértéket átlép, a neuron "tüzel", kimenete 1, különben 0.^[4] Ezt a neuronmodellt használta a Rosenblatt-perceptron, mely a 20. század közepén hatékony képfelismerő algoritmus volt.^[5]

A perceptron hátránya, hogy kettőnél több réteg esetén a tanítása nehezen kivitelezhető, ugyanis azok a gradiensereszkedések, melyek egy veszteségfüggvényt próbálnak iteratív módon minimalizálni, és ehhez a függvény gradiensével számolnak, alkalmatlanak a nem differenciálható küszöblogika tanítására. Más tanító algoritmusok (pl. differenciál-evolúció, hegymászó algoritmus) pedig a gradiensereszkedéshez képest sokkal lassabban konvergálnak. A kettőnél több rétegű (rejtett rétegeket tartalmazó) perceptron esetében a rejtett réteg tanítása szintén egy nehéz probléma, akkor is, ha a küszöblogikát a modernebb szigmoid jellegű aktivációs függvényeket alkalmazó szigmoidneuronokra cseréljük. Egy évtizeddel később bebizonyították, hogy a többrétegű, küszöblogikán alapuló perceptron csupán lineáris döntési határ képzésére képes, függetlenül attól, hogy hány réteggel látják el azt.^[6] A leírt nehézségekből fakadóan a mesterséges intelligencia kutatásban beköszöntött egy kevéssé termékeny időszak.

A mesterséges intelligencia telét a hiba-visszaterjesztés algoritmus (backpropagation of errors) leírása törte meg, mely lehetővé tette a rejtett rétegeket tartalmazó, differenciálható aktivációs függvénnyel ellátott neurális hálózatok tanítását gradiensereszkedéssel. Az új felfedezés, a számítási kapacitás exponenciális növekedése és a videókártyák lineáris algebra gyorsítóinak általános célú felhasználhatósága (GPGPU) lehetővé tette új neurális architektúrák feltalálását és azok gyakorlati alkalmazását.

További fontosabb közlemények, architektúrák a teljesség igénye nélkül:

• LSTM (Hosszú-rövid távú memória): forradalmasította a visszacsatolásos (rekurrens) architekturákat, csökkentve a gradiens robbanás jelenség visszatartó hatását visszacsatolás alkalmazása esetén. Idősorok (pl. hang, szöveg, kézírás) analízisében használatos architektúra.^[7]
• CNN (Konvolúciós neurális hálózat): a képanalitikában használatos, filtereket képes megtanulni.^[8]
• ReLU (aktivációs függvény): először tette lehetővé, hogy felügyeletlen előtanítás alkalmazása nélkül tanítsanak mély neurális hálózatokat, kiküszöbölve a szigmoid aktivációs függvények okozta gradiens-robbanás és gradiens-elhalás jelenségeket.^[9]
• Adam (Adaptív lendület becslés): a gradiensereszkedést kiterjesztő tanító algoritmus, mely napjainkra lényegében felváltotta az eredeti optimalizálót.^[10]
• GAN (Generatív párharc hálózat): két szembeállított neurális hálózat, generátor és diszkriminátor, az előbbi mintákat generál (pl. képeket), az utóbbi eldönti, hogy egy bemenetként átadott adat (kép) eredeti vagy a generátor által készített. A valóságoshoz megtévesztésig hasonló, de mégis egyedi minták (képek) létrehozására képes.^[11]

Neuronrétegek

A mesterséges neuron a neurális hálózat elemi számítási egysége, a biológiai neuron erősen leegyszerűsített modellje. A neuronokat általában nem önmagukban modellezzük, hanem sok ugyanolyan neuront egy rétegként értelmezünk, ekkor a legtöbb neurális számítás felírható mátrixműveletekként. A pontos művelet, amelyet egy adott réteg végez adja a réteg típusát, a hálózatban alkalmazott rétegek száma, típusa és sorrendje az adott neurális hálózat architektúrája.

Példák

Zárójelben az implementációkban, programkönyvtárakban gyakran használt neve a rétegnek.

• Teljesen kapcsolt réteg (Fully Connected, Dense, Linear Combination): előállítja a bemenetek és egy tárolt súlymátrix lineáris kombinációját: ${\displaystyle H=XW+b}$, ahol X a bemeneti mátrix, W a súlymátrix, b egy opcionális eltolósúly-vektor.
• Egyszerű rekurrens réteg (Recurrent, Simple recurrent): bemenetként visszakapja a saját kimenetét (az adatból képzett bemenet mellett): ${\displaystyle H_{t}=XW_{x}+b_{x}+H_{t-1}W_{h}+b_{h}}$, ahol X a bemeneti mátrix, W_x és b_x a hozzá tartozó súlyok, H_t-1 az előző kimenet, W_h, b_h a hozzá tartozó súlyok.
• Konvolúciós réteg (ConvXD, ahol X a bemenet dimenzióját jelöli, pl. Conv2D képek esetében): nincs teljes kapcsolás, a neuronok csak egy részét kapják a bemenetnek. Lényegében kereszt-korrelációt végez a neuronok súlymátrixával a bemeneti mátrixon: ${\displaystyle H=X*W+b}$, ahol ${\displaystyle *}$ a kereszt-korrelációt jelöli.
• Aktivációs réteg (Activation): a bemenetként kapott mátrixra vagy tenzorra elemenként hív egy aktivációs függvényt: ${\displaystyle H=g(X)}$.

A neurális hálózatok felépítése

A neuronrétegek anatómiája

3-4-2 neuronszámú, három rétegű, teljesen kapcsolt mesterséges neurális hálózat. Különböző színekkel a hálózat fő részei kerültek megjelölésre.

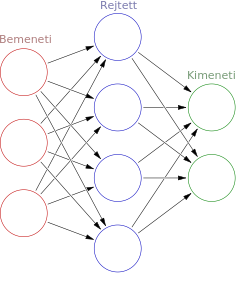
A neurális hálózatok rendszerint legalább három funkcionálisan és strukturálisan jól elkülöníthető részből állnak:

• Bementi réteg: módosítatlanul továbbítja a bemenetként átadott adatot a hálózat többi részének. Egy neurális hálózatnak több bemeneti rétege is lehet, ha elágazásokat is tartalmaz. A neuronok számát a bemeneti adat dimenzionalitása, alakja határozza meg.
• Rejtett rétegek: a bemenet és a kimenet között helyezkednek el, feladatuk az információ transzformációja, kódolása, illetve absztrakciók, köztes reprezentációk létrehozása. Számuk, típusuk, egymáshoz való kapcsolódásuk sorrendje és a bennük lévő neuronok száma változtatható paraméterei a hálózatnak.
• Kimeneti réteg: A kimeneti függvényt és a kimeneti neuronok számát az adott probléma jellege határozza meg. Osztályozás esetében jellemzően annyi kimeneti neuron van, ahány kategória áll a rendelkezésre, a kimeneti függvény pedig az adott osztályba tartozás valószínűségét hivatott reprezentálni a kategóriák között. Ilyen jellegű kimenet képzésére alkalmas a szigmoid és a SoftMax függvény. Regressziós probléma esetén kimeneti függvényt nem alkalmazunk, az utolsó rejtett réteg kimenetének lineáris kombinációját számítjuk ki. Egy neurális hálózatnak elméletileg több kimenete is lehet, ebben az esetben minden kimenethez társítani kell egy veszteségfüggvényt (lásd alább).

A kernel trükköt alkalmazó tanuló algoritmusoktól vett analógiával kijelenthetjük, hogy neurális hálózatok esetében a rejtett rétegek egy konfigurálható, tanulható kernelként működnek, ahol a kimeneti réteg az osztályozó.^[12]

Aktivációs függvények

A neuronrétegek között sokféle aktivációs függvényt alkalmazhatunk. Ezeket jellemzően elemenként értékeljük ki a bemeneti mátrixra, egyes különleges esetekben a bemenet többi elemével is számolunk.

• Szigmoid vagy logisztikus függvény: ${\displaystyle H={\frac {1}{1+e^{-X}}}}$. rejtett rétegek aktivációs függvényeként háttérbe szorult, mert szélsőségesen negatív vagy pozitív bemenet esetén a gradiense nagyon kis szám, ami csökkenti a tanítás hatékonyságát (gradiens elhalást idéz elő). 0 és 1 közé szorítja a bemenetet, így kimeneti rétegekben még használatos kétkategóriás osztályozás esetén és többkategóriás, többcímkés kategorizálásnál, ahol az egyes kategóriába való tartozás valószínűségét fejezhetjük ki vele.
• Hiperbolikus tangens: ${\displaystyle H=\tanh(X)={\frac {2}{1+e^{-2X}}}-1}$, a szigmoidhoz hasonló aktivációs függvény, melyet jellemzően rejtett rétegekben alkalmaznak. Mára modernebb függvények jórészt felváltották. A bemenetet -1 és +1 közé szorítja.
• ReLU (rektifikált lineáris egység):^[9] ${\displaystyle H=\max(0,X)}$. A rejtett rétegek között talán leggyakrabban használt aktivációs függvény. A negatív bemeneteket nullára állítja, a pozitívakat változatlanul hagyja. Bár 0-nál nincs deriváltja, de lebegőpontos számítás esetén rejtett rétegek között 0 bemeneti érték nagyon valószínűtlen és a gyakorlatban nem okoz problémát. Nem számításigényes és nem okoz gradiens-elhalást.
• Leaky ReLU (szivárgó ReLU): ${\displaystyle H=\max(\lambda X,X)}$. A ReLU esetében fellépő "Halott ReLU" jelenség kiküszöbölésére találták ki. Ha egy ReLU valamilyen okból akkora eltolósúlyt tanul meg, ami minden bemenetre 0 kimenetet képez, az a ReLU onnantól működésképtelenné válik, mert a gradiense is mindig 0 lesz. A szivárgó ReLU-ba épített szivárgási együttható (λ) egy tanulható paraméter, ideálisan 0 és 1 közötti szám.
• Softmax: ${\displaystyle H(z_{i})={\frac {e^{z_{i}}}{\sum _{j}e^{z_{j}}}}}$. Többkategóriás osztályozási problémák esetén használt kimeneti aktivációs függvény. A Softmax egy vektor bemenetű függvény, melyet a logisztikus regresszióban is használnak. Először kiszámítjuk az nevező exponenciális szummáját, majd az egyes elemeket exponenciálisát elosztjuk ezzel a szummával. Kimenetként egy olyan vektort kapunk vissza, amelynek elemei 0 és 1 közötti értékek és a vektor szummája 1, így a kimenet valószínűségeloszlásként értelmezzük, mely az egyes kategóriákba való tartozás valószínűségét adja meg, a maximum érték indexe pedig a legmagasabb valószínűségű kategória.

Veszteségfüggvények

A gradiensereszkedés kivitelezése végett választanunk kell egy olyan függvényt, mely deriválható és egy objektív számértékként összefoglalja a hálózat hibáját a kimenet és a várt kimenet ismeretében. Számos veszteségfüggvény létezik a gépi tanulás témakörében, neurális hálózatok esetében a leggyakrabban alkalmazott veszteségfüggvények a következők:

• Átlagos négyzetes eltérés (mean squared error): ${\displaystyle C={\frac {1}{2n}}\|O-Y\|^{2}}$. Szigmoid és softmax kimeneti aktivációs függvénnyel együtt lassan konvergál, ezért főleg regressziós problémák esetében használatos, lineáris aktivációs függvény mellett.
• Bináris kereszt-entrópia (binary cross-entropy): ${\displaystyle C=-{\frac {1}{n}}\sum _{i}{\big [}Y\log(O)+(1-Y)\log(1-O){\big ]}}$ kétkategóriás osztályozási probléma esetén szigmoid kimeneti függvény mellett használják.
• Többkategóriás kereszt-entrópia (multiclass cross-entropy): ${\displaystyle C=-\sum _{i}Y\log(O)}$. Gyakorlatilag a negatív log-likelihood értékét számítjuk ki vele. Információelméletben az információveszteség mértékét fejezi ki két bináris vektor között.

De a fentiek mellett alkalmazható a támasztóvektor-gépeknél használt Hinge-veszteségfüggvény vagy a Kullback-Leibler divergencia is.

Regularizációs technikák

A neurális hálózatok, különösen a mély architektúrák rendkívül ki vannak téve a statisztikai túlillesztés problémájának. Ennek kiküszöbölése végett regularizációs technikákat vethetünk be. Az alapelv az, hogy regularizált tanulás esetén a megtanult modell általánosabb lesz a regularizálatlan modellhez képest.

• L_p regularizáció: a súlyok P-normáját adjuk a veszteségfüggvényhez, általában L1 vagy L2 normát alkalmazunk. Ez a regularizáció arra készteti a hálózatot, hogy kis súlyokat tanuljon meg vagy ritkítsa a súlymátrixot (növelje a nulla súlyok számát). Ezeket a regularizációs tagokat egyszerűen hozzáadjuk a veszteségfüggvényhez és ellátjuk egy együtthatóval, amely az osztályozási pontosságból és a regularizációs tagból származó hibaérték egymáshoz képesti súlyozását képviseli (Lagrange-szorzó).
• Kiejtéses (Dropout) regularizáció:^[13] a neuronok egy véletlenszerűen kiválasztott halmazát kiejtjük a tanulási körből.
• Lecke-normalizálás (Batch normalization):^[14] a hálózat nyilvántart egy futó átlagot és egy futó szórást a bemenetekről, mellyel normalizálja az újonnan kapott bemeneteket. Drasztikusan csökkenthető ezzel a konvergencia sebessége és csökken a túlillesztés esélye is.

Optimalizálók

A tanuló fázisban meghatározzuk egy neurális hálózat kimenetének hibáját egy differenciálható hibafüggvénnyel, majd megbecsüljük az egyes súlyok hozzájárulását ehhez a hibához a hibafüggvény súlyok tekintetében vett gradiensének meghatározásával. Egyszerű esetben ezt a gradienst kivonjuk a súlyokból, ezzel olyan irányba módosítjuk a súlyokat, ami garantáltan csökkenti a veszteségfüggvényt. Azonban egyes esetekben a gradiens önmagában csak lassan képes biztosítani a konvergenciát. Ilyen esetekben a konvergencia meggyorsítására a gradiensereszkedés algoritmust különböző kiterjesztésekkel láthatjuk el, ezeket a technikákat, illetve a gradienssel nem is számoló egyéb technikákat nevezzük optimalizálóknak.

Tipikus gradiens alapú optimalizálók:

• Gradiensereszkedés: a súlyokból kivonjuk a veszteségfüggvény tekintetében vett gradiensüket.
• Lendület módszer: nyilvántartunk egy mozgó átlagot a gradiensekből (egy "súrlódással" csökkentett sebességet) és ezt vonjuk ki a súlyokból, mintha egy labdát gurítanánk le egy domboldalon.
• Nesterov lendület:^[15] hasonló a lendülethez, de először megtesszük a lépést a tárolt lendület mentén, utána számolunk gradienst és visszalépünk, ha romlott a pontosság.
• Adagrad:^[16] adaptív gradiens, minden súly részére tárol egy egyedi tanulási rátát, mely az adott súlyra számított összes eddigi gradiens négyzetösszege. Az aktuális tanulókörben számított gradienst ennek az értéknek a gyökével elosztja, így a sokáig alacsony gradienst kapó súlyok nagyobb lépést képesek tenni.
• RMSprop:^[17] gyökös átlagos négyzetes terjedés: Geoffrey Hinton (a mély tanulás keresztapja) adattudós nem publikált módszere, mely nyilvántart egy mozgó átlagot a gradiensek négyzetéből és ezzel módosítja súlyonként a tanulási rátát. A reziliens terjedés (Rprop) tanítási mód adaptációja részmintás tanulásra.
• Adam:^[10] adaptív lendület módszer: nyilvántartja a gradiensek mozgó átlagát (lendület) és a gradiensek négyzetének mozgó átlagát (memória), kombinálva az Adagrad és az RMSprop technikákat, és a memóriával módosított egyedi tanulási rátával megszorzott lendület alapján csökkenti a súlyok értékét. Általában ezt az optimalizálót ajánlják először alkalmazni egy új problémán.

Mély tanulás

A számítási kapacitás növekedésével a neurális hálózatok különféle területeken való feltörekvésével egyre összetettebb architektúrák jelennek meg, melyek jellegzetesen halmozzák egymásra a különböző típusú neuronrétegeket (mélyülnek) vagy változatos elágazásokat tartalmaznak. A neurális hálózatok mélységének növekedésével növekszik azok absztrakciós képessége, a különböző mélységi szinteken álló rétegek egyre összetettebb feladatok megoldására válnak képessé, azonban új típusú problémák megjelenésével járnak együtt.^[18]

A mély tanulás (Deep Learning) egy hívószó, mely a fenti problémakörre utal.

Tanítás

A mesterséges neurális hálózatok tanítása minden esetben egy felügyelt regressziós problémára kerül visszavezetésre, de kivitelezhető osztályozás és felügyeletlen tanítás is. A hálózatok működésében két fázist különíthetünk el: tanítási fázisban a ismert bemeneti paraméterek és várt kimenetek ismeretében a súlyokat változtatjuk úgy, hogy egy veszteségfüggvény értékét (például az átlagos négyzetes hibát) minimalizáljuk ezzel. A feltanított neurális hálózat a predikciós fázisban ezután ismeretlen bemenet átadásakor kimenetet képez, mely lehet például egy kategóriába való tartozás valószínűsége.

A jól leírható eset a három rétegű, összesítőként lineáris kombinációt, aktivációs függvényként valamilyen folytonos függvényt alkalmazó, előreterjesztéses (visszacsatolást nem tartalmazó) hálózat, amelynek esetében levezetjük a tanítás folyamatát.

Kimenetképzés

Tanításkor jellemzően nem egyetlen bemeneti vektort adunk át, hanem egy részmintát képzünk az adatainkból és azokra egyszerre határozzuk meg a veszteségfüggvényünk gradiensét, majd a kapott gradienseket átlagoljuk az egyes súlyokra. m részmintaméret és d dimenziós bemenet esetében tehát a bemenetünk a következő mátrix lesz: ${\displaystyle {\boldsymbol {X}}\in \mathbb {R} ^{m\times d}}$.

A hálózat rejtett rétegének súlyait és eltolósúlyait a következőképpen definiálhatjuk: ${\textstyle {\boldsymbol {W}}_{h}\in \mathbb {R} ^{d\times u},{\boldsymbol {b}}_{h}\in \mathbb {R} ^{u}}$, ahol W_h a súlymátrix, b_h pedig az úgynevezett eltolósúly-vektor.

A rejtett réteg által végzett művelet a következő: ${\displaystyle {\boldsymbol {H}}=g_{h}({\boldsymbol {X}}{\boldsymbol {W}}_{h}+{\boldsymbol {b}}_{h})}$, ahol g_h a rejtett réteg aktivációs függvényét jelöli. A bemeneti mátrixot megszorozva a súlymátrixszal, az eredeti bemenetet neurontérbe transzformáljuk. Az eltolósúly a bemenetekben fellelhető esetleges torzítás kiküszöbölése végett van jelen. A transzformáció eredményére elemenként a logisztikus függvényt hívjuk, mely 0 és 1 közé szorítja a kimenetet. A rejtett réteg kimenete, ${\displaystyle {\boldsymbol {H}}\in \mathbb {R} ^{m\times u}}$.

Az utolsó réteg a kimeneti réteg, melyet szintén egy súlymátrix és egy eltolósúly-vektor definiál: ${\displaystyle {\boldsymbol {W}}_{o}\in \mathbb {R} ^{u\times v},{\boldsymbol {b}}_{o}\in \mathbb {R} ^{v}}$, ahol v a kimeneti neuronok száma.

A kimeneti réteg a következő műveletet végzi: ${\displaystyle {\boldsymbol {O}}=g_{o}({\boldsymbol {HW}}_{o}+{\boldsymbol {b}}_{o})}$, ahol g_o a kimeneti réteg aktivációs függvényét jelöli.

Hiba meghatározása és visszaterjesztése

A hálózat kimenetének hibáját a várt kimenet ismeretében egy folytonos függvény, az úgynevezett veszteségfüggvény segítségével számszerűsítjük. A hálózat egyes súlyainak hozzájárulása a hibához a veszteségfüggvény súlyok tekintetében vett gradiensével egyenlő: ${\displaystyle \nabla _{w}C=\left\{{\frac {\partial C}{\partial w_{i}}}\right\}}$, ahol w a hálózat összes súlyát tartalmazó képzeletbeli vektor, C pedig a veszteségfüggvény (például az átlagos négyzetes eltérés).

A kimeneti réteg súlyai tekintetében vett gradiens a láncszabállyal határozható meg: ${\displaystyle {\frac {\partial C}{\partial W}}={\frac {\partial C}{\partial O}}{\frac {\partial O}{\partial W}}}$.

A rejtett rétegek hibájának meghatározásához alkalmaznunk kell a hiba-visszaterjesztést. Ehhez észre kell vennünk, hogy a lineáris kombinációig (tehát az aktivációs függvény hívása előttig) visszaszámított gradiens kétszer is felhasználásra kerül: egyrészt meghatározható általa a súlyok gradiense, másrészt az előző réteg kimenetének tekintetében vett gradiens, mely az előző réteg tanításához kell. A lineáris kombinációig visszaszámított gradiensre bevezetjük a delta-jelölést: ${\displaystyle \delta _{O}=\nabla _{O^{*}}C}$, ahol O^* a kimeneti réteg lineáris kombinációját jelöli, ${\displaystyle \delta _{O}}$pedig jelen definíció szerint a kimeneti réteg hibája vagy deltája és a következőképpen határozzuk meg: ${\displaystyle \delta _{O}={\frac {\partial C}{\partial O}}\odot g'(O)}$, aholg az aktivációs függvény deriváltja, melyet elemenként kiértékelünk az O mátrixra, ${\displaystyle \odot }$ pedig mátrixok elemenkénti szorzását jelöli. A delta jelöléssel felírjuk a kimeneti súlyok gradiensét:${\displaystyle \nabla _{W_{o}}C=\delta _{O}{\frac {\partial O}{\partial W_{o}}}=H^{T}\delta _{O}}$, ahol T felső indexben a transzponálást jelöli.

A rejtett réteg hibájának meghatározásához vissza kell terjeszteni a gradienst a rejtett réteg kimenetéig, majd kiszámítani a rejtett réteg deltáját, végül a deltából a súlyok gradiensét:

${\displaystyle {\frac {\partial C}{\partial H}}=\delta _{O}{\frac {\partial O}{\partial H}}=\delta _{O}W_{o}^{T}}$ eljuttat minket a rejtett réteg kimenetének gradienséig.

${\displaystyle \delta _{H}={\frac {\partial C}{\partial H}}\odot g'(H)}$ a rejtett réteg deltája (gradiens a lineáris kombinációnál).

${\displaystyle \nabla _{W_{h}}C=\delta _{H}{\frac {\partial H}{\partial W_{h}}}=X^{T}\delta _{H}}$ a rejtett réteg súlyainak gradiense.

Az eltolósúlyok gradiense ${\displaystyle \nabla _{b_{o}}C={\frac {\partial C}{\partial O}}{\frac {\partial O}{\partial b}}=\delta _{O}\times 1}$ és ${\displaystyle \nabla _{b_{h}}C={\frac {\partial C}{\partial H}}{\frac {\partial H}{\partial b}}=\delta _{H}\times 1}$.

Gradiensereszkedés

Ha neurális hálózat minden rétegének és minden súlyának meghatároztuk a gradiensét, a tanulási rátával (η) modulált gradiens kivonható a súlyok aktuális értékéből, így minden súlyt olyan irányba térítünk el, amely a veszteségfüggvény értékének csökkenéséhez vezet:

${\displaystyle W_{o}:=W_{o}-\eta \nabla _{W_{o}}C}$

${\displaystyle W_{h}:=W_{h}-\eta \nabla _{W_{h}}C}$

${\displaystyle b_{o}:=b_{o}-\eta \nabla _{b_{o}}C}$

${\displaystyle b_{h}:=b_{h}-\eta \nabla _{b_{h}}C}$

Ezzel zárul egy tanulási iteráció. A következő iterációban újra részmintát képzünk a tanuló adatsorból, kimenetet képzünk, hibát számolunk és visszaterjesztünk, majd gradiensereszkedést hajtunk végre. A tanuló adatsor egyszer teljes végigjárását nevezzük egy tanulókorszaknak. Az iteráció során a veszteségfüggvény kimenetét nyilvántartjuk és addig folytatjuk a tanítást, míg a veszteséget lehetőleg minimálisra csökkentjük. Ekkor elmondható, hogy az algoritmus egy minimumra konvergált.

Implementációk

• Tensorflow: szimbolikus számítási gráfok definíciójára és automatikus differenciálására használható, Google által fejlesztett könyvtár, mely neurális operációkat is tartalmaz. Python, C++ és más nyelveken elérhető könyvtárként.
• Theano Archiválva 2020. november 8-i dátummal a Wayback Machine-ben: a Tensorflow-hoz hasonló könyvtár, a Montreáli Egyetem fejlesztésében. Pythonon elérhető könyvtárként.
• CNTK: Microsoft Cognitive Toolkit, a Microsoft által fejlesztett szimbolikus könyvtár. Python, C++ és más programnyelveken elérhető könyvtárként.
• Keras: Tensorflow-ra, Theano-ra vagy CNTK-ra épülő, kifejezetten mély tanuláshoz és neurális hálózatok gyors definíciójához, CPU-n és GPU-n történő futtatásához használható, Python nyelvhez elérhető könyvtár.
• Torch: Lua nyelvre elérhető neurális hálózat és gépi tanulás könyvtár.
• Caffe: Pythonon és MATLAB-on is futni képes, neurális hálózatok és számítások definiálhatóak vele JSON-szerű szintaxissal.
• Brainforge: szimbolikus gráfokat nem alkalmazó, csupán mátrix-műveletekként definiált neurális hálózat könyvtár Python programnyelvhez.

További hivatkozások

• TensorFlow alapozó Könnyen érthető magyar nyelvű cikksorozat mesterséges neurális hálózatokról Python mintakódokkal (Tensorflow/Keras programkönyvtár használatával)

Jegyzetek

1. Balázs Csanád Csáji (2001) Approximation with Artificial Neural Networks; Faculty of Sciences; Eötvös Loránd University, Hungary
2. http://binds.cs.umass.edu/papers/1992_Siegelmann_COLT.pdf
3. Hebb, D. (1949) The Organization of Behavior. New York: Wiley & Sons.
4. McCulloch, & Pitts. (1943). A LOGICAL CALCULUS OF THE IDEAS IMMANENT IN NERVOUS ACTIVITY. Bulletin of Mathematical Biophysics, Vol. 5. , 115-133.
5. Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model For Information Storage And Organization In The Brain. Psychological Review Vol. 65 (6), 386–408.
6. Minsky, M., & Papert, S. (1969). Perceptrons: An Introduction to Computational Geometry. Cambridge: The MIT Press.
7. Hochreiter, Sepp (1997. november 1.). „Long Short-Term Memory”. Neural Computation 9 (8), 1735–1780. o. DOI:10.1162/neco.1997.9.8.1735.
8. LeCun, Yann; Léon Bottou; Yoshua Bengio; Patrick Haffner (1998). "Gradient-based learning applied to document recognition" (PDF). Proceedings of the IEEE. 86 (11): 2278–2324. doi:10.1109/5.726791. Retrieved October 7, 2016
9. Xavier Glorot, Antoine Bordes and Yoshua Bengio (2011). Deep sparse rectifier neural networks (PDF). AISTATS.
10. Kingma, D. P., & Ba, J. L. (2015). Adam: a Method for Stochastic Optimization. International Conference on Learning Representations, 1–13. https://arxiv.org/abs/1412.6980
11. Goodfellow, Ian; Pouget-Abadie, Jean; Mirza, Mehdi; Xu, Bing; Warde-Farley, David; Ozair, Sherjil; Courville, Aaron; Bengio, Joshua (2014). "Generative Adversarial Networks". arXiv:1406.2661  cs.LG.
12. Archivált másolat. [2017. december 22-i dátummal az eredetiből archiválva]. (Hozzáférés: 2017. december 22.)
13. Hinton, Geoffrey E.; Srivastava, Nitish; Krizhevsky, Alex; Sutskever, Ilya; Salakhutdinov, Ruslan R. (2012). "Improving neural networks by preventing co-adaptation of feature detectors". arXiv:1207.0580  cs.NE.
14. https://arxiv.org/abs/1502.03167
15. Nesterov, Y. (1983). A method for unconstrained convex minimization problem with the rate of convergence o(1/k2). Doklady ANSSSR (translated as Soviet.Math.Docl.), vol. 269, pp. 543– 547.
16. http://jmlr.org/papers/v12/duchi11a.html
17. Archivált másolat. [2016. november 23-i dátummal az eredetiből archiválva]. (Hozzáférés: 2017. december 22.)
18. Bengio, Y. (2009). Learning Deep Architectures for AI. Foundations and Trends in Machine Vol. 2. (1) , 1-127.

• Informatikai portál • összefoglaló, színes tartalomajánló lap