GL
All
Articles
Dictionary
Quotes
Map

Wikiwand ❤️ Wikipedia

PrivacyTerms
Medida da irracionalidade

Medida da irracionalidade

unha medida da irracionalidade dun número real x é unha medida do perto que se pode aproximar mediante racionais From Wikipedia, the free encyclopedia

Medida da irracionalidade
•
•
•
•
•
Expoñente da irracionalidadeAlgúns casosCorolariosLímites coñecidosNotasVéxase taménBibliografíaOutros artigosLigazóns externas

En matemáticas, unha medida da irracionalidade dun número real x {\displaystyle x} {\displaystyle x} é unha medida do "preto" que se pode aproximar mediante racionais.

Thumb
Aproximacións racionais á raíz cadrada de 2.

Se unha función f ( t , λ ) {\displaystyle f(t,\lambda )} {\displaystyle f(t,\lambda )}, definida para t , λ > 0 {\displaystyle t,\lambda >0} {\displaystyle t,\lambda >0}, toma valores reais positivos e é estritamente decrecentes en ambas as variábeis, considere a seguinte desigualdade:

0 < | x − p q | < f ( q , λ ) {\displaystyle 0<\left|x-{\frac {p}{q}}\right|<f(q,\lambda )} {\displaystyle 0<\left|x-{\frac {p}{q}}\right|<f(q,\lambda )}

para un número real dado x ∈ R {\displaystyle x\in \mathbb {R} } {\displaystyle x\in \mathbb {R} } e números racionais p q {\displaystyle {\frac {p}{q}}} {\displaystyle {\frac {p}{q}}} con p ∈ Z , q ∈ Z + {\displaystyle p\in \mathbb {Z} ,q\in \mathbb {Z} ^{+}} {\displaystyle p\in \mathbb {Z} ,q\in \mathbb {Z} ^{+}}. Definimos R {\displaystyle R} {\displaystyle R} como o conxunto de todos os λ ∈ R + {\displaystyle \lambda \in \mathbb {R} ^{+}} {\displaystyle \lambda \in \mathbb {R} ^{+}} para o que só existen un número finito de p q {\displaystyle {\frac {p}{q}}} {\displaystyle {\frac {p}{q}}} de forma que se satisfaga a desigualdade. Entón λ ( x ) = inf R {\displaystyle \lambda (x)=\inf R} {\displaystyle \lambda (x)=\inf R} chámase unha medida da irracionalidade de x {\displaystyle x} {\displaystyle x} en relación a f . {\displaystyle f.} {\displaystyle f.} Se non hai tal λ {\displaystyle \lambda } {\displaystyle \lambda } e o conxunto R {\displaystyle R} {\displaystyle R} está baleiro, x {\displaystyle x} {\displaystyle x} dise que ten unha medida de irracionalidade infinita λ ( x ) = ∞ {\displaystyle \lambda (x)=\infty } {\displaystyle \lambda (x)=\infty }.

En consecuencia, a desigualdade

0 < | x − p q | < f ( q , λ ( x ) + ε ) {\displaystyle 0<\left|x-{\frac {p}{q}}\right|<f(q,\lambda (x)+\varepsilon )} {\displaystyle 0<\left|x-{\frac {p}{q}}\right|<f(q,\lambda (x)+\varepsilon )}

ten como moito só un número de finitamente moitas solucións p q {\displaystyle {\frac {p}{q}}} {\displaystyle {\frac {p}{q}}} para tódolos ε > 0 {\displaystyle \varepsilon >0} {\displaystyle \varepsilon >0}.

Expoñente da irracionalidade

O expoñente de irracionalidade ou medida de irracionalidade de Liouville-Roth vén dado pola función f ( q , μ ) = q − μ {\displaystyle f(q,\mu )=q^{-\mu }} {\displaystyle f(q,\mu )=q^{-\mu }}, unha definición que adapta a definición dos números de Liouville, o expoñente de irracionalidade μ ( x ) {\displaystyle \mu (x)} {\displaystyle \mu (x)} defínese para números reais x {\displaystyle x} {\displaystyle x} sendo o supremo do conxunto de μ {\displaystyle \mu } {\displaystyle \mu } tal que se satisfán as desigualdades 0 < | x − p q | < 1 q μ {\displaystyle 0<\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}} {\displaystyle 0<\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}} por un número infinito de pares de enteiros primos ( p , q ) {\displaystyle (p,q)} {\displaystyle (p,q)} con q > 0 {\displaystyle q>0} {\displaystyle q>0}.[1][2]:246

Para calquera valor n < μ ( x ) {\displaystyle n<\mu (x)} {\displaystyle n<\mu (x)}, o conxunto infinito de todos os racionais p / q {\displaystyle p/q} {\displaystyle p/q} que satisfán a desigualdade anterior producen boas aproximacións de x {\displaystyle x} {\displaystyle x}. Pola contra, se n > μ ( x ) {\displaystyle n>\mu (x)} {\displaystyle n>\mu (x)}, entón hai como moito finitamente moitos coprimos ( p , q ) {\displaystyle (p,q)} {\displaystyle (p,q)} con q > 0 {\displaystyle q>0} {\displaystyle q>0} que satisfán a desigualdade.

Outro xeito de expresalo sería[3]

μ ( x ) := inf { μ ( x ) ≥ 0 : só hai finitamente moitos racionais  p / q  tal que  | x − p q | < 1 q μ } . {\displaystyle \mu (x):=\inf {\bigg \{}\mu (x)\geq 0:{\text{só hai finitamente moitos racionais }}p/q{\text{ tal que }}\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}{\bigg \}}.} {\displaystyle \mu (x):=\inf {\bigg \{}\mu (x)\geq 0:{\text{só hai finitamente moitos racionais }}p/q{\text{ tal que }}\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}{\bigg \}}.}
μ ( x ) := sup { μ ( x ) ≥ 0 : hai infinitamente moitos racionais  p / q  tal que  | x − p q | < 1 q μ } . {\displaystyle \mu (x):=\sup {\bigg \{}\mu (x)\geq 0:{\text{hai infinitamente moitos racionais }}p/q{\text{ tal que }}\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}{\bigg \}}.} {\displaystyle \mu (x):=\sup {\bigg \{}\mu (x)\geq 0:{\text{hai infinitamente moitos racionais }}p/q{\text{ tal que }}\left|x-{\frac {p}{q}}\right|<{\frac {1}{q^{\mu }}}{\bigg \}}.}

Algúns casos

Por exemplo, sempre que unha aproximación racional p q ≈ x {\displaystyle {\frac {p}{q}}\approx x} {\displaystyle {\frac {p}{q}}\approx x} con p , q ∈ N {\displaystyle p,q\in \mathbb {N} } {\displaystyle p,q\in \mathbb {N} } dá n + 1 {\displaystyle n+1} {\displaystyle n+1} cifras decimais exactas, entón

1 10 n ≥ | x − p q | ≥ 1 q μ ( x ) + ε {\displaystyle {\frac {1}{10^{n}}}\geq \left|x-{\frac {p}{q}}\right|\geq {\frac {1}{q^{\mu (x)+\varepsilon }}}} {\displaystyle {\frac {1}{10^{n}}}\geq \left|x-{\frac {p}{q}}\right|\geq {\frac {1}{q^{\mu (x)+\varepsilon }}}}

para calquera ε > 0 {\displaystyle \varepsilon >0} {\displaystyle \varepsilon >0}, agás como máximo un número finito de pares "afortunados" ( p , q ) {\displaystyle (p,q)} {\displaystyle (p,q)}.

Un número x ∈ R {\displaystyle x\in \mathbb {R} } {\displaystyle x\in \mathbb {R} } con expoñente de irracionalidade μ ( x ) ≤ 2 {\displaystyle \mu (x)\leq 2} {\displaystyle \mu (x)\leq 2} chámase número diofantiano,[4] mentres que os números con μ ( x ) = ∞ {\displaystyle \mu (x)=\infty } {\displaystyle \mu (x)=\infty } chámanse números de Liouville.

Corolarios

  • Os números racionais teñen un expoñente de irracionalidade 1, mentres que (como consecuencia do teorema da aproximación de Dirichlet) todo número irracional ten un expoñente de irracionalidade polo menos 2.
  • Por outra banda, unha aplicación do lema de Borel-Cantelli mostra que case todos os números, incluídos todos os números irracionais alxébricos, teñen un expoñente de irracionalidade exactamente igual a 2.[2] :246
  • Temos μ ( x ) = μ ( r x + s ) {\displaystyle \mu (x)=\mu (rx+s)} {\displaystyle \mu (x)=\mu (rx+s)} para números reais x {\displaystyle x} {\displaystyle x} e números racionais r ≠ 0 {\displaystyle r\neq 0} {\displaystyle r\neq 0} e s {\displaystyle s} {\displaystyle s}. Se para algúns x {\displaystyle x} {\displaystyle x} temos μ ( x ) ≤ μ {\displaystyle \mu (x)\leq \mu } {\displaystyle \mu (x)\leq \mu }, entón dedúcese que μ ( x 1 / 2 ) ≤ 2 μ {\displaystyle \mu (x^{1/2})\leq 2\mu } {\displaystyle \mu (x^{1/2})\leq 2\mu }.[5]:368 
  • Para un número real x {\displaystyle x} {\displaystyle x} dado pola súa expansión de fracción continua simple x = [ a 0 ; a 1 , a 2 , . . . ] {\displaystyle x=[a_{0};a_{1},a_{2},...]} {\displaystyle x=[a_{0};a_{1},a_{2},...]} con converxentes p i / q i {\displaystyle p_{i}/q_{i}} {\displaystyle p_{i}/q_{i}} cúmprese:
μ ( x ) = 1 + lim sup n → ∞ ln ⁡ q n + 1 ln ⁡ q n = 2 + lim sup n → ∞ ln ⁡ a n + 1 ln ⁡ q n . {\displaystyle \mu (x)=1+\limsup _{n\to \infty }{\frac {\ln q_{n+1}}{\ln q_{n}}}=2+\limsup _{n\to \infty }{\frac {\ln a_{n+1}}{\ln q_{n}}}.} {\displaystyle \mu (x)=1+\limsup _{n\to \infty }{\frac {\ln q_{n+1}}{\ln q_{n}}}=2+\limsup _{n\to \infty }{\frac {\ln a_{n+1}}{\ln q_{n}}}.}

Se temos que o lim sup n → ∞ 1 n ln ⁡ | q n | ≤ σ {\displaystyle \limsup _{n\to \infty }{\tfrac {1}{n}}{\ln |q_{n}|}\leq \sigma } {\displaystyle \limsup _{n\to \infty }{\tfrac {1}{n}}{\ln |q_{n}|}\leq \sigma } e lim n → ∞ 1 n ln ⁡ | q n x − p n | = − τ {\displaystyle \lim _{n\to \infty }{\tfrac {1}{n}}{\ln |q_{n}x-p_{n}|}=-\tau } {\displaystyle \lim _{n\to \infty }{\tfrac {1}{n}}{\ln |q_{n}x-p_{n}|}=-\tau } para algúns números reais positivos σ , τ {\displaystyle \sigma ,\tau } {\displaystyle \sigma ,\tau }, entón podemos estabelecer un límite superior para o expoñente de irracionalidade de x {\displaystyle x} {\displaystyle x} con: [6][7]

μ ( x ) ≤ 1 + σ τ {\displaystyle \mu (x)\leq 1+{\frac {\sigma }{\tau }}} {\displaystyle \mu (x)\leq 1+{\frac {\sigma }{\tau }}}.

Límites coñecidos

  • Se μ ( x ) = 1 , x   {\displaystyle \mu (x)=1,x\ } {\displaystyle \mu (x)=1,x\ } é racional.
  • Se μ ( x ) = 2 , x   {\displaystyle \mu (x)=2,x\ } {\displaystyle \mu (x)=2,x\ } é alxébrico de grao > 1.
  • Se μ ( x ) ≥ 2 , x   {\displaystyle \mu (x)\geq 2,x\ } {\displaystyle \mu (x)\geq 2,x\ } é trascendental.

Para a maioría dos números transcendentais, non se coñece o valor exacto do seu expoñente de irracionalidade.[5] A continuación móstrase unha táboa de límites superiores e inferiores coñecidos.

Máis información Número ...
Número x {\displaystyle x} {\displaystyle x} Expoñente da irracionalidade μ ( x ) {\displaystyle \mu (x)} {\displaystyle \mu (x)} Notas
Límite inferior Límite superior
Número racional p / q {\displaystyle p/q} {\displaystyle p/q} con p ∈ Z , q ∈ Z + {\displaystyle p\in \mathbb {Z} ,q\in \mathbb {Z} ^{+}} {\displaystyle p\in \mathbb {Z} ,q\in \mathbb {Z} ^{+}} 1 Todo número racional p / q {\displaystyle p/q} {\displaystyle p/q} ten un expoñente de irracionalidade de exactamente 1.
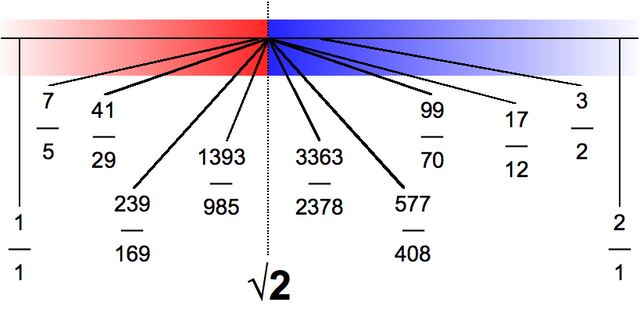
Número alxébrico irracional α {\displaystyle \alpha } {\displaystyle \alpha } 2 Polo Teorema de Roth o expoñente de irracionalidade de calquera número alxébrico irracional é exactamente 2. Exemplos inclúen raíces cadradas e o número áureo φ {\displaystyle \varphi } {\displaystyle \varphi }.
e 2 / k , k ∈ Z + {\displaystyle e^{2/k},k\in \mathbb {Z} ^{+}} {\displaystyle e^{2/k},k\in \mathbb {Z} ^{+}} 2 Se os elementos a n {\displaystyle a_{n}} {\displaystyle a_{n}} da expansión simple da fracción continua dun número irracional x {\displaystyle x} {\displaystyle x} están limitados por encima de a n < P ( n ) {\displaystyle a_{n}<P(n)} {\displaystyle a_{n}<P(n)} por un polinomio arbitrario P {\displaystyle P} {\displaystyle P}, entón o seu expoñente de irracionalidade é μ ( x ) = 2 {\displaystyle \mu (x)=2} {\displaystyle \mu (x)=2}.

Os exemplos inclúen números nos que as fraccións continuas se comportan de forma previsíbel como

e = [ 2 ; 1 , 2 , 1 , 1 , 4 , 1 , 1 , 6 , 1 , . . . ] {\displaystyle e=[2;1,2,1,1,4,1,1,6,1,...]} {\displaystyle e=[2;1,2,1,1,4,1,1,6,1,...]} e I 0 ( 2 ) / I 1 ( 2 ) = [ 1 ; 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , . . . ] {\displaystyle I_{0}(2)/I_{1}(2)=[1;2,3,4,5,6,7,8,9,10,...]} {\displaystyle I_{0}(2)/I_{1}(2)=[1;2,3,4,5,6,7,8,9,10,...]}.

tan ⁡ ( 1 / k ) , k ∈ Z + {\displaystyle \tan(1/k),k\in \mathbb {Z} ^{+}} {\displaystyle \tan(1/k),k\in \mathbb {Z} ^{+}} 2
tanh ⁡ ( 1 / k ) , k ∈ Z + {\displaystyle \tanh(1/k),k\in \mathbb {Z} ^{+}} {\displaystyle \tanh(1/k),k\in \mathbb {Z} ^{+}} 2
S ( b ) {\displaystyle S(b)} {\displaystyle S(b)} con b ≥ 2 {\displaystyle b\geq 2} {\displaystyle b\geq 2} 2 S ( b ) := ∑ k = 0 ∞ b − 2 k {\displaystyle S(b):=\sum _{k=0}^{\infty }b^{-2^{k}}} {\displaystyle S(b):=\sum _{k=0}^{\infty }b^{-2^{k}}}con b ∈ Z {\displaystyle b\in \mathbb {Z} } {\displaystyle b\in \mathbb {Z} }, ten termos de fracción continua que non superan unha constante fixa.[8][9]
T ( b ) {\displaystyle T(b)} {\displaystyle T(b)} con b ≥ 2 {\displaystyle b\geq 2} {\displaystyle b\geq 2}[10] 2 T ( b ) := ∑ k = 0 ∞ t k b − k {\displaystyle T(b):=\sum _{k=0}^{\infty }t_{k}b^{-k}} {\displaystyle T(b):=\sum _{k=0}^{\infty }t_{k}b^{-k}} onde t k {\displaystyle t_{k}} {\displaystyle t_{k}} é a secuencia de Thue-Morse e b ∈ Z {\displaystyle b\in \mathbb {Z} } {\displaystyle b\in \mathbb {Z} }. Ver Constante de Prouhet-Thue-Morse .
ln ⁡ ( 2 ) {\displaystyle \ln(2)} {\displaystyle \ln(2)}[11][12] 2 3.57455... Hai outros números da forma ln ⁡ ( a / b ) {\displaystyle \ln(a/b)} {\displaystyle \ln(a/b)} para os que se coñecen os límites dos seus expoñentes de irracionalidade.[13][14][15]
ln ⁡ ( 3 ) {\displaystyle \ln(3)} {\displaystyle \ln(3)}[11][16] 2 5.11620...
5 ln ⁡ ( 3 / 2 ) {\displaystyle 5\ln(3/2)} {\displaystyle 5\ln(3/2)}[17] 2 3.43506... Hai moitos outros números da forma 2 k + 1 ln ⁡ ( 2 k + 1 + 1 2 k + 1 − 1 ) {\displaystyle {\sqrt {2k+1}}\ln \left({\frac {{\sqrt {2k+1}}+1}{{\sqrt {2k+1}}-1}}\right)} {\displaystyle {\sqrt {2k+1}}\ln \left({\frac {{\sqrt {2k+1}}+1}{{\sqrt {2k+1}}-1}}\right)} para os que se coñecen límites no seu expoñente de irracionalidade.[17] Este é o caso de k = 12 {\displaystyle k=12} {\displaystyle k=12}.
π / 3 {\displaystyle \pi /{\sqrt {3}}} {\displaystyle \pi /{\sqrt {3}}}[18][19] 2 4.60105... Hai moitos outros números da forma 2 k − 1 arctan ⁡ ( 2 k − 1 k − 1 ) {\displaystyle {\sqrt {2k-1}}\arctan \left({\frac {\sqrt {2k-1}}{k-1}}\right)} {\displaystyle {\sqrt {2k-1}}\arctan \left({\frac {\sqrt {2k-1}}{k-1}}\right)} para os que se coñecen límites no seu expoñente de irracionalidade.[18] Este é o caso de k = 2 {\displaystyle k=2} {\displaystyle k=2}.
π {\displaystyle \pi } {\displaystyle \pi }[11][20] 2 7.10320... Probouse que se a Serie Flint Hills ∑ n = 1 ∞ csc 2 ⁡ n n 3 {\displaystyle \displaystyle \sum _{n=1}^{\infty }{\frac {\csc ^{2}n}{n^{3}}}} {\displaystyle \displaystyle \sum _{n=1}^{\infty }{\frac {\csc ^{2}n}{n^{3}}}} (onde n está en radiáns) converxe daquela o expoñente de irracionalidade de π {\displaystyle \pi } {\displaystyle \pi } é como moito 5 / 2 {\displaystyle 5/2} {\displaystyle 5/2}[21][22] e que se diverxe o expoñente de irracionalidade é como mínimo 5 / 2 {\displaystyle 5/2} {\displaystyle 5/2}.[23]
π 2 {\displaystyle \pi ^{2}} {\displaystyle \pi ^{2}}[11][24] 2 5.09541... π 2 {\displaystyle \pi ^{2}} {\displaystyle \pi ^{2}} e ζ ( 2 ) {\displaystyle \zeta (2)} {\displaystyle \zeta (2)} son linearmente dependentes sobre Q {\displaystyle \mathbb {Q} } {\displaystyle \mathbb {Q} }.
arctan ⁡ ( 1 / 2 ) {\displaystyle \arctan(1/2)} {\displaystyle \arctan(1/2)}[25] 2 9.27204... Hai moitos outros números da forma arctan ⁡ ( 1 / k ) {\displaystyle \arctan(1/k)} {\displaystyle \arctan(1/k)} para os que se coñecen límites no seu expoñente de irracionalidade.[26][27]
arctan ⁡ ( 1 / 3 ) {\displaystyle \arctan(1/3)} {\displaystyle \arctan(1/3)}[28] 2 5.94202...
Constante de Apéry ζ ( 3 ) {\displaystyle \zeta (3)} {\displaystyle \zeta (3)}[11] 2 5.51389...
Γ ( 1 / 4 ) {\displaystyle \Gamma (1/4)} {\displaystyle \Gamma (1/4)}[29] 2 10330
Constante de Cahen C {\displaystyle C} {\displaystyle C}[30] 3
Constante de Champernowne C b {\displaystyle C_{b}} {\displaystyle C_{b}} ien base b ≥ 2 {\displaystyle b\geq 2} {\displaystyle b\geq 2}[31] b {\displaystyle b} {\displaystyle b} Examplos inclúen C 10 = 0.1234567891011... = [ 0 ; 8 , 9 , 1 , 149083 , 1 , . . . ] {\displaystyle C_{10}=0.1234567891011...=[0;8,9,1,149083,1,...]} {\displaystyle C_{10}=0.1234567891011...=[0;8,9,1,149083,1,...]}
Números de Liouville L {\displaystyle L} {\displaystyle L} ∞ {\displaystyle \infty } {\displaystyle \infty } Os números de Liouville son precisamente aqueles números que teñen un expoñente de irracionalidade infinito.[2]:248
Pechar

Notas

  1. [1]
    Parshin, A. N.; Shafarevich, I. R. (2013-03-09). Number Theory IV: Transcendental Numbers (en inglés). Springer Science & Business Media. ISBN 978-3-662-03644-0.
  2. [2]
    Bugeaud, Yann (2012). Distribution modulo one and Diophantine approximation. Cambridge Tracts in Mathematics 193. Cambridge: Cambridge University Press. ISBN 978-0-521-11169-0. MR 2953186. Zbl 1260.11001. doi:10.1017/CBO9781139017732.
  3. [3]
    Robin Pemantle. "irrationality" (PDF).
  4. [4]
    Tao, Terence (2009). "245B, Notes 9: The Baire category theorem and its Banach space consequences". What's new. Consultado o 2024-09-08.
  5. [5]
    Borwein, Jonathan M. (1987). Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity. Wiley.
  6. [6]
    Masayoshi Hata (1993). Acta Arith., ed. "Rational approximations to π and some other numbers (Lema 2.1)". 63, No. 4: 335-349.
  7. [7]
    Chudnovsky, G. V. (1982). "Hermite-padé approximations to exponential functions and elementary estimates of the measure of irrationality of π". En Chudnovsky, David V.; Chudnovsky, Gregory V. The Riemann Problem, Complete Integrability and Arithmetic Applications. Lecture Notes in Mathematics (en inglés) 925. Berlin, Heidelberg: Springer. pp. 299–322. ISBN 978-3-540-39152-4. doi:10.1007/BFb0093516.
  8. [8]
    Shallit, Jeffrey (1979-05-01). "Simple continued fractions for some irrational numbers". Journal of Number Theory 11 (2): 209–217. ISSN 0022-314X. doi:10.1016/0022-314X(79)90040-4.
  9. [9]
    Shallit, J. O (1982-04-01). "Simple continued fractions for some irrational numbers, II". Journal of Number Theory 14 (2): 228–231. ISSN 0022-314X. doi:10.1016/0022-314X(82)90047-6.
  10. [10]
    Bugeaud, Yann (2011). "On the rational approximation to the Thue–Morse–Mahler numbers". Annales de l'Institut Fourier 61 (5): 2065–2076. ISSN 1777-5310. doi:10.5802/aif.2666.
  11. [11]
    Weisstein, Eric W. "Irrationality Measure". mathworld.wolfram.com. Consultado o 2020-10-14.
  12. [12]
    Nesterenko, Yu. V. (2010-10-01). "On the irrationality exponent of the number ln 2". Mathematical Notes (en inglés) 88 (3): 530–543. ISSN 1573-8876. doi:10.1134/S0001434610090257.
  13. [13]
    Wu, Qiang (2003). "On the Linear Independence Measure of Logarithms of Rational Numbers". Mathematics of Computation 72 (242): 901–911. ISSN 0025-5718. JSTOR 4099938. doi:10.1090/S0025-5718-02-01442-4.
  14. [14]
    Bouchelaghem, Abderraouf; He, Yuxin; Li, Yuanhang; Wu, Qiang (2024-03-01). "On the linear independence measures of logarithms of rational numbers. II". J. Korean Math. Soc. 61 (2): 293–307. doi:10.4134/JKMS.j230133.
  15. [15]
    Sal’nikova, E. S. (2008-04-01). "Diophantine approximations of log 2 and other logarithms". Mathematical Notes 83 (3): 389–398. ISSN 1573-8876. doi:10.1134/S0001434608030097.
  16. [16]
    "Symmetrized polynomials in a problem of estimating of the irrationality measure of number ln 3". www.mathnet.ru. Consultado o 2020-10-14.
  17. [17]
    Polyanskii, Alexandr (2015-01-27). "On the irrationality measure of certain numbers". arXiv:1501.06752 [math.NT].
  18. [18]
    Polyanskii, A. A. (2018-03-01). "On the Irrationality Measures of Certain Numbers. II". Mathematical Notes 103 (3): 626–634. ISSN 1573-8876. doi:10.1134/S0001434618030306.
  19. [19]
    Androsenko, V. A. (2015). "Irrationality measure of the number pi/sqrt(3)". Izvestiya: Mathematics 79 (1): 1–17. ISSN 1064-5632. doi:10.1070/im2015v079n01abeh002731.
  20. [20]
    Zeilberger, Doron; Zudilin, Wadim (2020-01-07). "The irrationality measure of π is at most 7.103205334137...". Moscow Journal of Combinatorics and Number Theory 9 (4): 407–419. arXiv:1912.06345. doi:10.2140/moscow.2020.9.407.
  21. [21]
    Alekseyev, Max A. (2011). "On convergence of the Flint Hills series". arXiv:1104.5100 [math.CA].
  22. [22]
    Weisstein, Eric W. "Flint Hills Series". MathWorld.
  23. [23]
    Meiburg, Alex (2022). "Bounds on Irrationality Measures and the Flint-Hills Series". arXiv:2208.13356 [math.NT].
  24. [24]
    Zudilin, Wadim (2014-06-01). "Two hypergeometric tales and a new irrationality measure of ζ(2)". Annales mathématiques du Québec 38 (1): 101–117. ISSN 2195-4763. arXiv:1310.1526. doi:10.1007/s40316-014-0016-0.
  25. [25]
    Bashmakova, M. G.; Salikhov, V. Kh. (2019). "Об оценке меры иррациональности arctg 1/2". Чебышевский сборник 20 (4 (72)): 58–68. ISSN 2226-8383.
  26. [26]
    Tomashevskaya, E. B. "On the irrationality measure of the number log 5+pi/2 and some other numbers". www.mathnet.ru. Consultado o 2020-10-14.
  27. [27]
    Salikhov, Vladislav K.; Bashmakova, Mariya G. (2022). "On rational approximations for some values of arctan(s/r) for natural s and r, s". Moscow Journal of Combinatorics and Number Theory 11 (2): 181–188. ISSN 2220-5438. doi:10.2140/moscow.2022.11.181.
  28. [28]
    Salikhov, V. Kh.; Bashmakova, M. G. (2020-12-01). "On Irrationality Measure of Some Values of $\operatorname{arctg} \frac{1}{n}$". Russian Mathematics 64 (12): 29–37. ISSN 1934-810X. doi:10.3103/S1066369X2012004X.
  29. [29]
    Waldschmidt, Michel (2008). "Elliptic Functions and Transcendence". Surveys in Number Theory. Developments in Mathematics 17. Springer Verlag. pp. 143–188. Consultado o 2024-09-10.
  30. [30]
    Duverney, Daniel; Shiokawa, Iekata (2020-01-01). "Irrationality exponents of numbers related with Cahen's constant". Monatshefte für Mathematik 191 (1): 53–76. ISSN 1436-5081. doi:10.1007/s00605-019-01335-0.
  31. [31]
    Amou, Masaaki (1991-02-01). "Approximation to certain transcendental decimal fractions by algebraic numbers". Journal of Number Theory 37 (2): 231–241. ISSN 0022-314X. doi:10.1016/S0022-314X(05)80039-3.

Véxase tamén

Bibliografía

Outros artigos

  • Serie Flint Hills.
  • Constante de Apéry
  • Teorema de Lindemann-Weierstrass
  • Teorema de Roth

Ligazóns externas

  • Irrationality Measure (MathWorld).
Edit in WikipediaRevision historyRead in Wikipedia

Wikiwand - on

Seamless Wikipedia browsing. On steroids.