Paradoxe de Bertrand

Le paradoxe de Bertrand est un problème en théorie des probabilités qui met en évidence les limites du recours à l'intuition dans cette discipline. Il consiste à prendre au hasard une corde d'un cercle donné et d'estimer la probabilité que celle-ci soit de longueur supérieure au côté du triangle équilatéral inscrit dans le cercle. Le paradoxe est que cette probabilité dépend du protocole de choix de la corde.

Ce problème fut énoncé pour la première fois en 1889 par Joseph Bertrand dans son ouvrage Calcul des probabilités^[1]. Bertrand en donnait trois réponses différentes (une chance sur deux, une sur trois et une sur quatre), toutes les trois apparemment valides.

Énoncé

Soit un cercle de rayon 1. Le côté d'un triangle équilatéral inscrit dans ce cercle a pour longueur ${\displaystyle {\sqrt {3}}}$. Le paradoxe de Bertrand consiste à déterminer la probabilité qu'une corde du cercle, choisie au hasard, possède une longueur supérieure à ${\displaystyle {\sqrt {3}}}$.

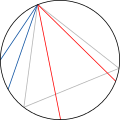
1. Extrémités aléatoires : soit un point de la circonférence du cercle et le triangle équilatéral inscrit dont l'un des sommets est ce point. On choisit aléatoirement un autre point sur le cercle et on considère la corde reliant les deux points. Elle est plus longue que le côté du triangle si le deuxième point est situé sur l'arc reliant les deux sommets du triangle opposé au premier point. La probabilité est donc alors 1/3.
2. Rayon aléatoire : on choisit un rayon du cercle et on considère le triangle équilatéral inscrit dont un côté est perpendiculaire au rayon. On choisit aléatoirement un point sur le rayon et on trace la corde dont il est le milieu. Cette corde est plus longue que le côté du triangle si le point est situé entre le centre du cercle et l'intersection du côté avec le rayon, laquelle est située au milieu de ce dernier. La probabilité est donc alors 1/2.
3. Milieu aléatoire : soit un point choisi aléatoirement à l'intérieur du cercle, on considère la corde dont il est le milieu, ou un diamètre du cercle si le point choisi est le centre. Cette corde est plus longue qu'un côté du triangle équilatéral inscrit si le point est situé à l'intérieur d'un cercle concentrique de rayon 1/2. L'aire de ce cercle est un quart de celle du grand cercle. La probabilité est donc alors 1/4.

• 
  1^re méthode.
• 
  2^e méthode.
• 
  3^e méthode.

Les cordes en rouge sont plus longues que le côté du triangle, celles en bleu plus courtes.

Explication

Le paradoxe de Bertrand met en évidence la dépendance à la méthode de sélection d'une corde « au hasard ». Dès que cette méthode est spécifiée, le problème possède une solution bien définie. En l'absence d'une telle méthode, le terme « au hasard », dans « prendre une corde du cercle au hasard », est ambigu. Les trois solutions présentées par Bertrand correspondent à des méthodes de sélection distinctes et valables, et en l'absence d'autre information, il n'y a aucune raison d'en privilégier une par rapport aux autres.

Une autre façon de visualiser les méthodes consiste à considérer la distribution des milieux des cordes. En dehors des diamètres, une corde est entièrement définie par son milieu. Chacune des trois méthodes de Bertrand conduit à une distribution des milieux différentes : les deux premières méthodes produisent deux distributions non uniformes distinctes, la troisième une distribution uniforme des milieux à l'intérieur du cercle. D'autres distributions peuvent être imaginées, conduisant à des probabilités encore différentes^[2].

• 
  Milieux de cordes choisies au hasard par la méthode 1.
• 
  Milieux de cordes choisies au hasard par la méthode 2.
• 
  Milieux de cordes choisies au hasard par la méthode 3.

• 
  Cordes choisies au hasard par la méthode 1.
• 
  Cordes choisies au hasard par la méthode 2.
• 
  Cordes choisies au hasard par la méthode 3.

Une explication claire du paradoxe se trouve dans l'article de N.C. Petroni^[3], ou encore (pour les méthodes 1 et 3) dans les notes de cours de Jean-François Le Gall^[4].

Notes et références

1. Joseph Bertrand, Calcul des probabilités, Gauthier-Villars, 1889, p. 5-6.
2. Michel Henry et Henri Lombardi, « Paradoxes et lois de probabilités », Repères, n^o 13,‎ octobre 1993 (lire en ligne)
3. (en) N. C. Petroni, « Thou shalt not say "at random" in vain: Bertrand's paradox exposed », sur arXiv.org de Cornell university library, 2019
4. Jean-François Le Gall, « Intégration, Probabilités et Processus aléatoires. », notes de cours à l'ENS de Paris.,‎ septembre 2006, pp 96-97. (lire en ligne [PDF])

Voir aussi

• Espace probabilisable

• Portail des probabilités et de la statistique