Loading AI tools
De Wikipédia, l'encyclopédie libre
Marino ou, en dalmate[1] Marin Ghetaldi, Ghetaldus, Ghetalde (en latin Marinus Ghetaldus) ou en croate Marin Getaldić est un mathématicien, physicien et homme politique de la république de Raguse, né le [Note 1] ou 1566 à Raguse (aujourd'hui Dubrovnik en Croatie), mort le ou 1627[Note 2] dans la même ville.
| Naissance |
Raguse ( république de Raguse) |
|---|---|
| Décès |
(à 57 ans) Raguse (République de Raguse) |
| Domaines | Algèbre appliquée à la géométrie |
|---|---|
| Institutions | Académie des Lyncéens |

C'est l'un des très rares élèves de François Viète avec Nathanael Tarporley, Jean de Beaugrand, Jacques Aleaume et l'Écossais Alexander Anderson[2] avec qui il est en contact étroit. Géomètre parmi les mathématiciens à l'origine de l'émergence de l'algèbre nouvelle, il est aussi l'un des premiers à apporter sa contribution à la géométrie analytique[3]. En correspondance avec Galilée et Clavius, il communique aux mathématiciens italiens, Paolo Sarpi, Antonio Santini, Carlo Renaldini, etc. cette nouvelle façon de noter les questions algébriques et la met en œuvre lui-même dans la reconstruction des œuvres d'Apollonios de Perga. En physique, il laisse une étude de miroirs paraboliques, et une de ses réalisations (71 cm de diamètre, 146 cm de hauteur) se trouve au musée de la marine à Londres[4]. Écrivain croate de langue latine[5], son souvenir demeure présent dans les rues de l'actuelle Dubrovnik, où il est présenté comme l'« Apollonios de Perga » croate[6].
Né dans une famille patricienne et nombreuse, originaire de Tarente[7] en Italie, Marino Ghetaldi est l'un des six enfants de Maro Marino Jacques Ghetaldi et d'Ana Andrée Resti[8]. Ses quatre frères, André, Simon, Jacques et Martolicu, ainsi que sa sœur Niki, habitent derrière l'église Saint-Blaise, près du palais du recteur, siège du gouvernement de la république de Raguse. En dépit de sa noblesse, c'est une famille peu fortunée et Niki devient religieuse à sa majorité[8]. Ghetaldi est d'abord l'élève des Franciscains de Raguse, dont l'école est située à la porte ouest de la ville. Le prêtre Ivan Simunov (Jean Siméon) lui y enseigne la grammaire et la littérature. Plus tard, Andreas Gallus, Nicolas di Matteo, Ivan Hristoforov (Jean Christophore) et Victor Basaljic lui enseignent les mathématiques[9],[8]. Il fréquente ensuite les cercles universitaires regroupés autour de Flora Zuzori, beauté qui est chantée par de nombreux poètes, où se retrouvent l'astronome Nicolas Nalješković, le philosophe-chancelier Nicolas Gučetić, les poètes Victor Beselji et Didacus Pyrrhus ainsi que l'historien pan-slave Mavro Orbin.
À dix-huit ans, Ghetaldi entre au Grand Conseil, l'organe législatif de la République, en tant que greffier, et mène dès lors de front ses carrières administrative et scientifique. Son travail concerne essentiellement les armes et la vente du sel, dont six mois sur la péninsule de Janjina, où il est suspendu pendant un temps pour avoir méconnu les lois[8].
En 1597, il abandonne ses responsabilités du district de Sabbioncello et accompagne son ami Marino Gucetic (di Gozzi), le neveu du banquier anglais Nicolas Gozzi[Note 3], dans ses voyages. Ils vont à Rome où Ghetaldi est l'élève de Clavius ; en Angleterre, où il demeure deux ans en compagnie de Marino Gucetic et se lie avec Francis Bacon ; puis en 1599 à Anvers où il complète sa formation auprès de Michel Coignet et de Federico Saminiati[Note 4] de Lucques.

Proposé à un poste de professeur de mathématiques à l'université de Louvain, qu'il décline, il vient à Paris (vers 1600) et rencontre François Viète dont il devient l'ami. Le mathématicien des Parthenay lui communique quelques-uns de ses ouvrages, dont son Harmonicon Celeste[10] et comme le maître des requêtes d'Henri IV manque de temps pour s'occuper de ses propres travaux mathématiques, Ghetaldi publie chez David Leclerc son Apollonius Gallus (l'Apollonius français) et son De Numerosa Potestatum[11],[12],[13].
Une lettre de la main de Marino Ghetaldi, datée du , et destinée à son maître, Michel Coignet, illustre le respect qu'il porte au géomètre français.
« Me trouvant à Paris pour d'autres affaires personnelles, j'ai voulu, avant de partir pour l'Italie, lui faire visite. Sa connaissance m'a prouvé qu'il était non moins affable que savant. Non seulement il m'a montré beaucoup de ses ouvrages encore inédits, mais il me les a confiés, afin que je les visse dans ma maison et à ma commodité. J'ai pu ainsi étudier plusieurs traités de son algèbre nouvelle, qui m'ont ouvert une lumière telle qu'il me paraît voir une foule de choses sans lesquelles je me considérerais comme aveugle. »
— Lettre à Coignet, le 15 février 1600[14].
Par la suite, Ghetaldi devient un adepte de cette façon d'écrire les mathématiques, qui permet de passer de l'étude des cas particuliers à la résolution générale de familles entières de problèmes, mis en équations selon le procédé décrit par Viète.
L'année suivante (1601), il revient à Raguse par l'Italie[Note 5] et séjourne à Padoue, où il se lie avec Paolo Sarpi[15] chez le seigneur bibliophile Gian Vincenzo Pinelli (en compagnie du Français Pessot[7]). Il y rencontre Galilée avec lequel il demeure par la suite en correspondance régulière[16],[17]. Il suit son enseignement et Galilée lui dévoile son compas, que Ghetaldi se propose de copier. Après un an, il quitte Padoue, et finit par arriver à Rome vers 1602. Il y rencontre notamment le mathématicien-jésuite Luca Valerio, membre de l’académie des Lyncéens, ami de Galilée, et jésuite napolitain et anti-copernicien.
Son premier ouvrage, le seul en tant que physicien, le Promotus Archimedes seu de variis corporum generibus gravitate et magnitudine comparatis (en latin : L’Exposé d'Archimède relatif à la densité des corps pesants et la comparaison de leur grandeur) (en abrégé Promotus Archimedes), est imprimé en 1603. Dédicacé au cardinal Olivario, il porte sur les graves et sous prétexte de présenter la physique d'Archimède, Ghetaldi y donne ses propres mesures des densités de l'or, du mercure, de l'argent, du cuivre, du fer, de l'étain... mais également de l'eau, du vin, de l'huile, de la cire et du miel[18]. Il le fait avec grande précision, démontrant à l'aide de l'algèbre spécieuse des propositions sur les mélanges d'or et d'argent (le problème dit de la couronne de Héron II) qui jusque-là n'ont été traités que de façon rhétorique[19]. Son second ouvrage, Non nullae propositiones de parabola (sur la Parabole), dédicacé au jésuite de Bamberg, sort à Rome la même année (1603). Ghetaldi y définit les paraboles comme sections d'un cône de révolution.

Vers la fin de l'année 1603, il connaît néanmoins quelques démêlés avec la justice sans que la cause en soit connue. Ses biographes ne connaissent pas non plus l'origine de ses ressources (un riche héritage en Angleterre lui est attribué[6]), ni le rôle auprès de lui de Marino Gučetić de Gozzi, qui semble l'avoir accompagné dans chacun de ses déplacements pendant six ans. Ghetaldi s'échappe lui-même de Rome via Venise et revient alors à Raguse, où il reprend sa place dans le grand et le petit conseil de la république. Nommé juge à la cour d'appel en 1604, il est dans cette période chargé par le Sénat de veiller aux habitants de la ville de Ston atteints de paludisme. Cette ville, source de revenus importants pour Raguse grâce aux salines de la Neretva et de la presqu’île de Pelješac, est protégée des menaces de l'Empire ottoman et de Venise, par des remparts extérieurs sur plus de 5 kilomètres, et intérieurs sur 900 mètres[Note 6]. Il entreprend la consolidation de la tour semi-circulaire, Pozvizd[20], qui domine les fortifications de Ston. Sa nomination à la reconstruction des remparts de Ston a été acquise deux ans plus tôt par 22 voix contre 12 et une abstention[21]. Ghetaldi ne peut en revanche échapper à la maladie. Après une période de soins, il est parmi les envoyés du Sénat de la république auprès de Constantinople en 1606. Cette mission est jugée périlleuse, et la rumeur court qu'il y a laissé la vie. Cette rumeur court encore plusieurs années après ce voyage[22]. De nouveau à Raguse, et en correspondance avec les mathématiciens Christopher Grienberger, Clavius[23], Galilée et Paul Guldin, il se trouve, selon ses propres mots :
« Dans un coin du monde où l'on ne voit jamais de Gazette mathématique[24]. »
Paul Guldin, qui apprécie ses travaux, tente de le persuader d'éditer les œuvres complètes de Viète à Munich[6].
En 1607, il publie à Venise l'Apollonius redivivus seu restituta Apollonii Pergaei inclinationum geometria (restauration du livre d’Apollonios de Perga sur l'inclination), de nouveau dédicacé au cardinal Olivario[7], et le Supplementum Apollonii Galli seu exsuscitata Apollonii Pergaei tactionum geometriae pars reliqua (supplément à l'Apollon Français de François Viète), dédicacé à Paolo Emilio Cesi[7], marquis de Riano et neveu du cardinal Pier Donato Cesi[25], ainsi qu'un petit livre, Variorum problematum collectio (collection de problèmes variés), dédié à Marino Gozzi[7] et contenant 42 problèmes de géométrie et leurs solutions. Marino Ghetaldi écrit[26] :
« Je te dédie ce livre, à toi avec qui j'ai traversé pendant six ans la quasi-totalité de l'Europe. Et à dire vrai, je ne sais si personne connaît mieux que toi les préoccupations de mon esprit. »
En 1613, il publie Apollonius redivivus seu restituta Apollonii Pergaei se inclinationibus geometriae liber secundus (Le second livre des inclinations d'Apollonios de Perga), et entretient pendant quelque temps une polémique avec Clément Cyriaque de Mangin, à laquelle participe également son ami écossais Alexander Anderson et dans laquelle il s'agit de défendre la mémoire de François Viète.

Après son séjour à Constantinople, où il cherche en vain des manuscrits traduits du grec en arabe, Ghetaldi se spécialise dans l'élaboration d'instruments d'optique, miroirs paraboliques et télescopes. Il mène ses expériences dans une grotte demeurée célèbre encore aujourd'hui[27]. Le peuple et les marins le prennent alors pour un « mage » un peu fou. Dans une lettre à Clavius, il se flatte dès 1608 de pouvoir faire fondre sous le soleil le plomb, l'argent, et l'acier au foyer de son miroir, ce qui suppose une température de 1 200 °C[28],[29]. La même année (1608), le , il écrit à Galilée qu'il est comme enterré vivant à Raguse :
« Io sono qui come sepolto[30]. »
Chargé de l'office des vins, puis de la laine, et enfin consul pour les litiges civils et de nouveau juge à la cour d'appel, il est autorisé à revenir à Rome en 1620.
Il y vit un an, et est élu l'année suivante (sans jamais y siéger officiellement car l'Académie ne sait où il loge[31]) à l'Académie des Lyncéens. À cette époque les membres de l'Académie sont étroitement surveillés par le Saint-Office et Ghetaldi repart pour Raguse sans que l'Académie en sache les raisons[32].
En 1625, dans une lettre datée du , il écrit au « plus vieil ami qui lui reste », le mathématicien jésuite Christopher Grienberger, comment il se propose de mesurer le diamètre de la Terre à l'aide de calculs sur les triangles sphériques. Il meurt alors qu'il prépare un nouveau voyage pour Rome[33] afin de réaliser ce rêve d'arpenteur.
Marino Ghetaldi a épousé Marijom (ou Maria) Sorkočević, morte en couches, dont il a eu trois filles : Anica, Franica et Maria.
Il a également pour amis le mathématicien jésuite Théodose Rubeo[34], alias Rossi, élève de Clavius[35],[Note 7], le richissime botaniste Gian Vincenzo Pinelli et le mathématicien-astronome Paolo Sarpi, qui laisse de lui ce portrait[36] : « Ange pour le costume (les mœurs), démon pour les mathématiques. »

Il est également lié au cardinal Serafino Olivario, prélat d'origine française, conseiller juridique et confident du pape[7]. Parmi ses amis, se trouve le poète écossais orientaliste George Strachan[37], qui vient à Paris en 1592, puis à Rome, et pousse ses périples linguistiques[38] jusqu'à Anah (seul est conservé son Album amicorum).
Quelques auteurs dont Montucla puis Maximilien Marie[39] dans son Histoire des sciences mathématiques et physiques affirment à tort que la mission dont il fut chargé près du Sultan interrompit ses travaux et qu'il ne revint pas de Constantinople.
Un distique lui est attribué, gravé sur la propriété des Ghetaldi :
« Restez à l'écart. Ne vous inquiétez pas de la jalousie, des disputes, ni de la vanité. Paix et tranquillité ornent la grotte, les jardins et les rochers. »
Enfin, dans sa préface au Promotus, il affirme modestement[40] :
« Is enim ego sum qui malim scire quam nosci, discere quam docere. »
L'œuvre de Ghetaldi s'étend dans de nombreuses directions. Elle se situe à la charnière[41] entre le moment des grandes innovations de la fin du XVIe siècle et celui où vont véritablement se fixer les outils de l'algèbre et de la mécanique. Ghetaldi fait partie de ces générations intermédiaires, avec lesquelles il correspond, celles de Johannes Kepler, de Paul Guldin, de Willebrord Snell, de Jacques Aleaume, d'Albert Girard mais aussi de Jean de Beaugrand et d'Alexander Anderson ou de Paolo Sarpi, générations qui poursuivent les travaux de Copernic, de Viète, d'Harriot ou de Tycho Brahe, mais qui ne voient pas aboutir leurs efforts. Si Galilée se distingue d'eux par sa longévité, il est le seul qui peut recueillir une part du bénéfice de tant de travaux, dont le couronnement est l'œuvre des deux génération suivantes, avec Wallis, Fermat, Girard Desargues, Descartes, Frans van Schooten, Christian Huygens, Newton et pour finir Leibniz[42]. Il y a, par conséquent, quelque chose d'inachevé et de périphérique dans l'œuvre du mathématicien et physicien ragusain. Et cela n'est pas surprenant car son travail voit le jour à Raguse, dans une ville qui entre en déclin, située loin de tous les centres mathématiques, de sorte que, plusieurs fois dans sa vie, Ghetaldi manifeste la conscience de cet isolement. S'il publie, c'est à Paris, à Padoue, à Rome, à Venise, pas à Raguse. Quant à sa dernière œuvre, significativement, elle est publiée par ses filles à titre posthume via la chambre apostolique, à Rome, sous la protection du Cardinal Francesco Barberini, celui qui, trois ans après, tente en vain de protéger Galilée.
Car les travaux de Ghetaldi se développent à l'ombre de la compagnie de Jésus et de ses meilleurs soutiens, les deux mathématiciens pontificaux, Christopher Clavius et Christopher Grienberger, loin du foyer d'innovation qu'est à cette époque la Hollande protestante[43]. Son impossible affiliation à l’académie des Lyncéens marque d'ailleurs toute la difficulté pour les mathématiciens et physiciens italiens de la première moitié du XVIIe siècle de travailler en toute liberté, sans rendre de compte à Rome. Sarpi et Galilée ne connaissent-ils pas, dans les années 1610, le même type de difficultés à faire admettre leurs découvertes ? Il semble que Ghetaldi s'y soit plié de meilleure grâce qu'eux.
D'une façon plus particulière, Ghetaldi se fixe une limitation interne dans son approche des sciences, celle de restaurer — en latin, sa langue natale — les œuvres des anciens Grecs, et de le faire principalement à l'aide de l'outil géométrique. Alors que d'autres savants européens, un peu plus jeunes, plus loin de Rome, comme Albert Girard ou son ami Anderson se lancent dans la recherche de nouvelles inventions en algèbre, Ghetaldi tente de demeurer fidèle à ses premiers maîtres, Clavius et Coignet, ne faisant appel qu'en dernier ressort à l'algèbre nouvelle de Viète. Il le fait alors avec une grande dextérité ; si grande qu'il a pu être considéré parfois comme le précurseur de la géométrie analytique[41].
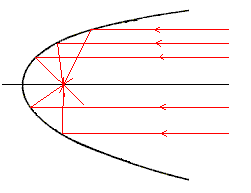
En sciences physiques, Ghetaldi accomplit plusieurs expériences sur la densité des matériaux, laissant d'excellentes mesures de ces densités ; il est également connu pour ses fabrications de verres teintés[44] ; son intérêt manifeste pour les miroirs et notamment les miroirs paraboliques, dont il décrit le foyer sont demeurés dans les mémoires ; outre ses ouvrages de poliorcétique, il est aussi connu pour ses tentatives de mesurer le rayon terrestre. Trente ans après près sa mort ses ouvrages sont toujours estimés et ses échelles de densités (publiées dans le Promotus Archimedes) sont encore reprises, notamment par Gaspar Schott, qui les intègre telles quelles dans sa Magia universalis de 1658.
En mathématiques, l'œuvre de Ghetaldi est encore plus considérable. Élève de Michel Coignet et de Christopher Clau[45], correspondant de Galileo Galilée et ami d'Alexander Anderson, il est un émule patient d'Apollonios de Perga et rédige deux livres à sa gloire. Mais surtout, il édite, popularise[46] et poursuit l'œuvre de Viète, qu'il complète par de nombreux ouvrages annonçant les découvertes de Pierre de Fermat et de Girard Desargues.
La plus importante contribution de Ghetaldi aux mathématiques est son application de l'algèbre à la géométrie, particulièrement dans son De resolutione et de compositione mathematica, libri quinque, publié à titre posthume par ses filles, Anna Francesca et Maria (elles publièrent ce livre en respectant la volonté de leur père de le dédicacer au Cardinal Francesco Barberini). Dans cet ouvrage, Ghetaldi annonce, dix ans avant, la Géométrie du philosophe de la Haye, et, huit ans avant, Pierre Hérigone et son mathematicus cursus. Cette publication a parfois été considérée comme le premier livre de géométrie analytique[47] jamais publié.

À la page 240 de cette dernière publication[48], apparaît notamment dans l'écriture aequabitur l'équation d'une conique[Note 8]. Remarquable également dans cet ouvrage la forme particulière du symbole « », proche d'une croix pattée ou d'une croix de Malte. On la trouvait déjà chez De Hortega (dans son Tractado subtillissimo de arithmetica y geometria, en 1552 et 1563), Guillaume Klebitius (en 1565) et Adrien Romain (en 1593), et on la retrouve chez René Descartes (en 1637)[49].
Dans les années qui suivent sa disparition, le travail mathématique de Ghetaldi influence particulièrement Paolo Sarpi, Antonio Santini[50], Jean de Beaugrand[46], Giovanni Camillo Glorioso et Carlo Renaldini[51], l'un des derniers Italiens à adopter le langage de l'algèbre nouvelle, ainsi que le mathématicien anglais William Oughtred, qui reprend une partie de ses résultats dans ses Opuscula mathematica.

Que ce soit par manque de temps, à cause de ses charges dans la République ou bien du peu d'importance qu'il attache à délimiter le champ de ses propositions, les travaux de Ghetaldi ne sont pas exempts d'incorrections ou d'erreurs[52]. De surcroît, il demeure prisonnier de la volonté de reconstruction des livres de l'Antiquité. Cette quête domine les mathématiques de la Renaissance tardive (jusqu'à Hérigone), et Ghetaldi n'y échappe pas. Comme ses prédécesseurs, Francesco Maurolico ou Marule, Viète, ou Snellius, Ghetaldi innove en croyant retrouver le véritable langage algébrique de Pappos, de Diophante, de Théon d'Alexandrie ou d’Apollonios de Perga. Au travers de cette redécouverte, dans un style tout nouveau, de l'Analyse d'Apollonios, la dépassant par là même singulièrement selon les mots de Jean Itard[53], Ghetaldi laisse entrevoir dans son dernier ouvrage, publié à titre posthume, les premiers développements de la géométrie analytique.
Pour autant, cette évolution ne se fait pas sans hésitation, ni combat. Elle commence en 1603, quand, dans son De Variorum, Ghetaldi résout trois sortes de problèmes par des méthodes purement géométriques. Il n'y donne pas toujours les conditions dans lesquelles s'appliquent ses résolutions.
Dans Nonnullae propositiones de parabola, Ghetaldi ne parvient pas non plus à démontrer parfaitement l'identité des paraboles obtenues par section d'un cône oblique et celles obtenues par section d'un cône de révolution[52].
Plus tard, dans Supplementum Apollonii Galli, il ne résout qu'imparfaitement le cinquième problème d'Apollonios.
Cette dernière erreur provoque la publication en 1612 par Alexander Anderson de son Supplementum Apollonii redivi[52]. Le traité de l'Écossais est alors apporté à Raguse par l'orientaliste George Strachan et donne lieu à une correction de Ghetaldi en 1613 dans son Apollonius redivivus seu restitutae Apollonü Pergaei de inclinationibus geometriae, liber secundus. Quoique leurs méthodes de résolution de ce cinquième problème d'Apollonios soient différentes, Ghetaldi marque dans sa préface tout le respect qu'il doit aux travaux de l'Écossais. Anderson, de son côté, dédicace à Ghetaldi la publication en 1615 de ses Zététiques des problèmes d'Apollonius. Une amitié mathématique se noue autour de l'héritage de Viète.
Mais, en 1616, Ghetaldi s'attire les foudres du mathématicien bourguignon Clément Cyriaque de Mangin[54] pour son ouvrage de 1603. Mangin (puis Jacob Christmann et ultérieurement de Michelangelo Ricci) lui reproche particulièrement ses erreurs dans la résolution d'un problème dû à Regiomontanus : De triangulis planis et sphaerecis (Des triangles plans et sphériques, première édition 1533).
Alors, en 1617, c'est Alexander Anderson qui défend Ghetaldi et l'honneur de l'école de François Viète (nommément cité par De Mangin), en publiant une réponse, cinglante, Animadversionis in Francisum Vietam a Clemento Cyriaco nuper brevis Διακρισις, contre Cyriaque. Anderson en complète d'ailleurs sa résolution, en 1619, dans Exercitationum mathematicorum decas primas.
Lorsqu'à la fin de sa vie, Ghetaldi revient une dernière fois sur cette démonstration défectueuse, il le fait avec la volonté de résoudre cette difficile question par de nouvelles méthodes. Cela se retrouve en effet dans son dernier ouvrage, le De resolutione et de compositione mathematica, libri quinque, qui s'ouvre par la liste des propositions à démontrer et donne les solutions algébriques à quelques problèmes d'Apollonios de Perga[55] que Ghetaldi a déjà résolus géométriquement (sans préciser les conditions limites des grandeurs en jeu) dans ses premières publications. Ghetaldi y reprend alors le cinquième problème d'Apollonios par les méthodes de l'algèbre nouvelle (sans citer les travaux qu'Anderson a consacrés à ce sujet en 1619, faute de les avoir reçus selon Ronald Calinger[52] car vraisemblablement, l'Écossais est mort entre-temps). Ce travail novateur, dans lequel apparaissent les premières traces de géométrie analytique, a fait l'objet d'études approfondies par Eugène Gelcich en 1882[Note 9].

De son vivant Ghetaldi publie six ouvrages mais son œuvre principale est publiée à titre posthume :
On lui doit également la construction d'un miroir parabolique conservé jusqu'au XIXe siècle dans les collections de la famille Barbarini, puis au musée maritime de Londres[56] ainsi qu'en 1604 la construction d'une tour Pozvizd, faisant partie du système de fortification de Raguse. Une publication de se œuvres a été réalisée pour le 400e anniversaire de sa naissance, on consultera à cet effet l'analyse que lui consacre Jean Grisard [57]

Ghetaldi est reconnu très tôt comme un des meilleurs géomètres et algébristes de son temps. Dès 1603, Henry Percy, le protecteur de Thomas Harriot et neuvième comte de Northumberland a entendu parler de lui[58]. Une certaine concurrence s'établit d'ailleurs autour d'Harriot à propos des mesures des densités. En France, moins de quatre ans après sa disparition, Pierre Hérigone donne, à la fin du premier volume de son Cursus Mathematicus, quatre problèmes sous le titre de La géométrie d'inclinations d'Apollonius Pergeus, restituée par Marinus Ghetaldus (Apollonii Pergaei inclinationum geometria, a Marino Ghetaldo restituta). Cet emprunt, qui va de la page 905 à 914 n'est autre que l’Apollonius redivivus seu restituta Apollonii Pergaei inclinationum geometria, ou du moins 4 problèmes de ce traité. Quant à Johannes Kepler, il le prise, selon ses lettres, comme l'égal de Galilée. Il est également apprécié par Mersenne et Claude Mydorge[59],[60].
À la fin du XVIIe siècle, les travaux de Marino Ghetaldi sont encore tenus en grande estime par de nombreux savants, notamment l'Anglais Edmond Halley et le Hollandais Christian Huygens. Le Français Montucla le cite encore dans son histoire, mais donne à Descartes toute la gloire de l'invention de la géométrie analytique. Au siècle suivant, Charles Bossut et Joseph-Louis Lagrange l'ont quasiment rayé de leur histoire des sciences[58]. Les Allemands lui rendent néanmoins hommage[58], notamment Abraham Gotthelf Kästner. En fait, son influence se maintient au XVIIIe siècle par l'entremise des Anglais, John Lawson[61], Samuel Horsley[62], Reuben Burrow[63] qui empruntent beaucoup à ses travaux[6]. Ils sont suivis au siècle suivant par Johann Wilhelm Camerer[64] et Daniel Schwenter[52].
Au XIXe siècle, Michel Chasles semble ignorer son importance et n'en parle qu'incidemment en marge de Viète[65]. Les Italiens Francesco Maria Appendini[66] et G. Barbieri lui rendent un hommage en 1802 puis 1840, dans leurs galeries de Ragusains illustres. Ils sont suivis seize ans plus tard par le Croate Simeone Gliubich. En 1868, l'éditeur de la Penny encyclopédie, Charles Knight, lui consacre quelques pages dans ses biographies[67] mais il faudra attendre la fin du XIXe siècle, avec Antonio Favaro, Heinrich Wieleitner (1874-1931)[68] et le Croate Eugène Gelcich (un professeur à l'école navale de Pola, en Autriche) pour que son rôle soit pleinement reconnu. Pour autant, ses œuvres n'ont toujours pas été traduites du latin.
Michael Sean Mahoney évoque dans The beginnings of algebraic thought[69] l'importance du De resolutione et compositione mathematica ; il lui rend un vibrant hommage dans The mathematical career of Pierre de Fermat, 1601-1665[70], précisant avec quels soins Ghetaldi accomplit les étapes zététique et poristique des problèmes géométriques qu'il a en vue, mais aussi la vigilance avec laquelle il suit dans leur exégèse, les étapes de la poristique. Mahonney juge par exemple qu’il se montre particulièrement utile dans la compréhension de théorèmes que Fermat laisse, quelques années plus tard, à la sagacité de son lecteur[71]. Plus récemment, son œuvre a été entièrement rééditée, et commentée, par l'astronome croate Zarko Dadic[72].
Dans sa patrie, la renommée de Marino Ghetaldi est longtemps demeurée à l'honneur : au XIXe, Raguse donne encore son nom à un navire et, de nos jours, il est un des rares mathématiciens à posséder sa page Facebook[réf. nécessaire], alors qu'il fait toujours la une des hebdomadaires locaux à la date anniversaire de sa mort (le 7 ou le )[Note 10].
Quant à la grotte, située au pied du mont Bergato, dans laquelle il travaillait à ses expériences d'optique, cette grotte de Raguse, où il menait ses expériences sur les miroirs, et reliée à sa villa par un escalier dérobé selon l'écrivain Andrew Archibald Paton[73], cette grotte qui lui conféra auprès des populations locales la réputation d'un ermite et d'un mage, elle porte depuis son surnom de bête[74].
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.