Développée
De Wikipédia, l'encyclopédie libre
En géométrie, la développée d'une courbe plane est le lieu de ses centres de courbure. On peut aussi la décrire comme l'enveloppe de la famille des droites normales à la courbe.
Histoire
Apollonius (aux environs de 200 av. J.-C.) a discuté des développées dans le Livre V de ses Coniques. Cependant, Huygens est parfois crédité pour avoir été le premier à les étudier (1673). Huygens a formulé sa théorie des développées vers 1659 pour aider à résoudre le problème de la recherche de la courbe tautochrone, qui à son tour l'a aidé à construire un pendule isochrone. En effet, la courbe tautochrone est une cycloïde et la cycloïde a la propriété unique que sa développée est également une cycloïde. La théorie des développées, en fait, a permis à Huygens d'obtenir de nombreux résultats qui seront plus tard trouvés en utilisant l'algèbre[1].
Développée d'une courbe paramétrique
Résumé
Contexte
On suppose la courbe suffisamment dérivable et birégulière. Si elle est paramétrée par l'abscisse curviligne sous la forme , le centre de courbure s'obtient en posant
où est le centre de courbure, la courbure et le vecteur normal au point .
Le vecteur dérivé de la développée est
en utilisant les formules de Frenet. On vérifie ainsi que :
- les points stationnaires de la développée g correspondent aux points où la dérivée de la courbure de f s'annule, en particulier les sommets de f (points de courbure extrémale) ;
- entre deux tels points, la tangente à la développée g au point de paramètre s est la normale à la courbe f.
Pour et on obtientet
Propriétés de la développée
Résumé
Contexte

Afin de dériver les propriétés d'une courbe régulière, il est avantageux d'utiliser la longueur de l'arc de la courbe donnée comme paramètre, car et (voir formules de Frenet-Serret). D'où le vecteur tangent de la développée est :
De cette équation on obtient les propriétés suivantes de la développée :
- Aux points avec la développée n'est pas régulière. Cela signifie qu'aux points de courbure maximale ou minimale (sommets de la courbe donnée) la développée a des cuspides (c'est ce qu'on observe sur les développées de parabole, d'ellipse, de cycloïde et de néphroïde).
- Pour tout arc de la développée qui n'inclut pas de cuspide, la longueur de l'arc est égale à la différence entre les rayons de courbure à ses extrémités. Ce fait conduit à une preuve simple du théorème de Tait-Kneser (en) sur l'emboîtement des cercles osculateurs[2].
- Les normales de la courbe donnée aux points de courbure non nulle sont des tangentes à la développée, et les normales de la courbe aux points de courbure nulle sont des asymptotes à la développée. Donc : la développée est l'enveloppe des normales de la courbe donnée.
- Aux sections de la courbe avec ou la courbe est une développante de sa développée. (Dans le diagramme : la parabole bleue est une développante de la parabole semi-cubique rouge, qui est en fait la développée de la parabole bleue).
- Deux courbes parallèles ont même développée.
Exemples
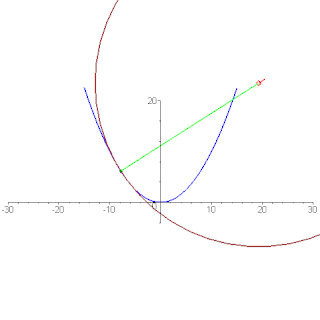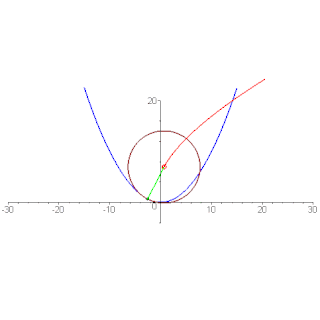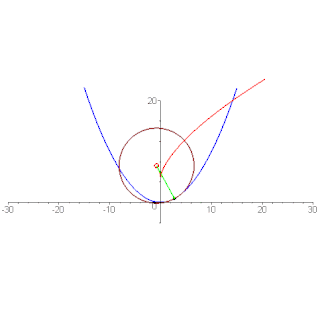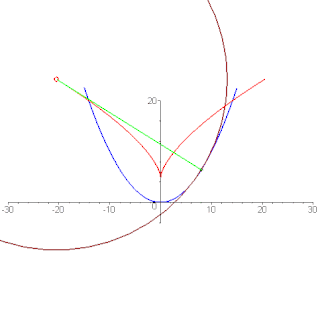
Développée d'une parabole
Pour la parabole avec la représentation paramétrique on obtient des formules au-dessus les équations : qui décrit une parabole semi-cubique.
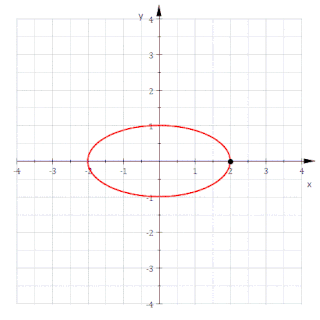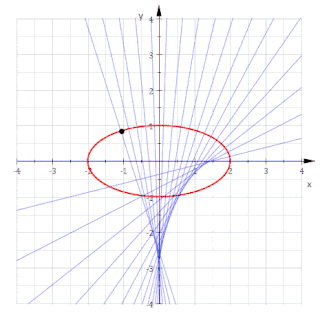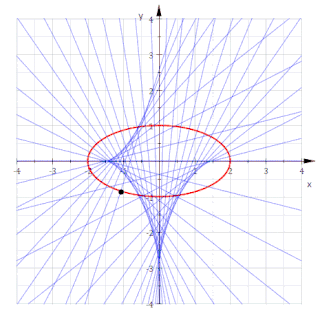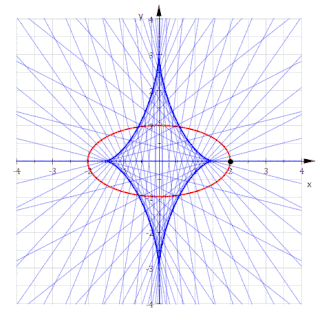
Développée d'une ellipse

Pour l'ellipse avec la représentation paramétrique on obtient[3] :
Ce sont les équations d'un astroïde non symétrique. Éliminer conduit à la représentation implicite

Développée d'une cycloïde
Pour la cycloïde avec la représentation paramétrique la développée sera : qui décrit une réplique transposée d'elle-même.
Développées de quelques courbes

La développée
- d'une parabole est une parabole semi-cubique (voir ci-dessus),
- d'une ellipse est un astroïde non symétrique (voir ci-dessus),
- d'une droite est un point à l'infini,
- d'un néphroïde est un néphroïde (moitié moins gros, voir schéma),
- d'un astroïde est un astroïde (deux fois plus grand),
- d'une cardioïde est une cardioïde (un tiers plus grande),
- d'un cercle est son centre,
- d'un deltoïde est un deltoïde (trois fois plus grand),
- d'une cycloïde est une cycloïde isométrique,
- d'une spirale logarithmique est la même spirale logarithmique,
- d'une tractrice est une chaînette.
Courbe radiale
Une courbe avec une définition similaire est la radiale d'une courbe donnée. Pour chaque point de la courbe, on prend le vecteur du point au centre de courbure, qu'on translate de sorte qu'il commence à l'origine. Alors le lieu des points à la fin de tels vecteurs est appelé la radiale de la courbe. L'équation de la radiale est obtenue en supprimant les termes x et y de l'équation de la développée. Cela produit
Voir aussi
Wikiwand - on
Seamless Wikipedia browsing. On steroids.







































