Dilatation (géométrie)

En mathématiques, en particulier en géométrie, une dilatation est une application linéaire ou affine, d'un espace vectoriel ou affine dans lui-même, se restreignant à l'identité dans un hyperplan et à une homothétie dans une droite supplémentaire, d'où l'autre nom donné d'affinité hyperplane^[1],[2].

1.	Apposez le bandeau sur les autres pages à fusionner : Transvection Affinité (mathématiques)	Utilisez ce texte : {{à fusionner |Dilatation (géométrie) |Transvection |Affinité (mathématiques)}}
2.	Important : ajoutez une section dans Pages à fusionner en motivant votre proposition.	Pour créer la section : Créer la section sur la page des Pages à fusionner
3.	Pensez à informer les contributeurs principaux de la page et les projets associés lorsque cela est possible.	Utilisez ce texte : {{subst:Avertissement fusion |Dilatation (géométrie) |Transvection |Affinité (mathématiques)}}

Cet article est à lire en parallèle avec celui sur les transvections.

• 
  Dessin d'origine.
• 
  Résultat par dilatation de direction horizontale.

Dilatation vectorielle

Définition

Une dilatation ${\displaystyle f}$ d'un K-espace vectoriel ${\displaystyle E}$ est une affinité de base un hyperplan ${\displaystyle H}$, et de rapport ${\displaystyle \lambda \in K}$ non nul.

Plus précisément, si ${\displaystyle D=Ku}$ est une droite supplémentaire de ${\displaystyle H}$ dans ${\displaystyle E}$, un vecteur ${\displaystyle x}$ de ${\displaystyle E}$ se décompose en ${\displaystyle x_{H}+h(x)u}$ suivant ${\displaystyle H\oplus D}$ (${\displaystyle h}$ est la forme linéaire "composante sur ${\displaystyle u}$"). La dilatation ${\displaystyle f}$ est définie par^[3],[4]:

${\displaystyle f(x)=x_{H}+\lambda h(x)u}$.

On obtient comme cas particuliers : l'identité pour ${\displaystyle \lambda =1}$, et les symétries hyperplanes (pour ${\displaystyle \lambda =-1}$) qui sont les réflexions dans le cas euclidien où ${\displaystyle H}$ et ${\displaystyle D}$ sont orthogonaux.

Propriétés

• Les dilatations sont bijectives : la réciproque de la dilatation ci-dessus est la dilatation de mêmes base et direction, et de rapport ${\displaystyle 1/\lambda }$.

• L'ensemble des dilatations de base et direction fixées forme un sous-groupe du groupe linéaire ${\displaystyle GL(E)}$, isomorphe au groupe multiplicatif ${\displaystyle K^{*}}$ du corps de base, par l'application qui à ${\displaystyle f}$ fait correspondre son rapport.

En dimension finie

• Le rapport ${\displaystyle \lambda }$ d'une dilatation n'est autre que son déterminant^[5].
• Si le corps de base a au moins 3 éléments, tout automorphisme de ${\displaystyle E}$ est produit de dilatations (autrement dit, ${\displaystyle GL(E)}$ est engendré par les dilatations)^{[5],[4],[1],[2],[6]}.
• Un automorphisme de ${\displaystyle E}$ est diagonalisable si et seulement s'il est produit commutatif de dilatations.

Caractérisations

Une dilatation de ${\displaystyle E}$ autre que l'identité est caractérisée par le fait que l'ensemble de ses vecteurs invariants est un hyperplan ${\displaystyle H}$ et que l'image d'un vecteur donné ${\displaystyle v}$n'appartenant pas à l'hyperplan se décompose en ${\displaystyle h+\lambda v}$ avec ${\displaystyle \lambda \neq 1}$ ; ${\displaystyle \lambda }$ est alors le rapport de la dilatation. Si ${\displaystyle \lambda =1}$, on obtient une transvection^[5].

Autrement dit, ${\displaystyle f\neq {\text{id}}\in GL(E)}$ est une dilatation ssi ${\displaystyle {\text{Ker}}(f-{\text{id}})}$ est un hyperplan et ${\displaystyle {\text{Im}}(f-{\text{id}})\not \subset {\text{Ker}}(f-{\text{id}})}$^[7].

En dimension finie, on a les autres caractérisations pour ${\displaystyle f\neq {\text{id}}}$ ^[6]:

• ${\displaystyle {\text{Ker}}(f-{\text{id}})}$ est un hyperplan et ${\displaystyle \det(f)\neq 1}$.
• ${\displaystyle {\text{Ker}}(f-{\text{id}})}$ est un hyperplan et ${\displaystyle f}$ est diagonalisable.

Matrice de dilatation

Dans une base de ${\displaystyle E\,}$ formée de vecteurs de la base et de la direction de la dilatation, la dilatation a pour matrice une matrice du type ${\displaystyle \operatorname {diag} (1,1,..,1,\lambda ,1,..,1)=I_{n}+(\lambda -1)E_{ii}\,}$. Ces matrices sont appelées matrices élémentaires de dilatation^[6].

Dilatation affine

Une dilatation d'un espace affine ${\displaystyle E}$ est une affinité de base un hyperplan affine (donc de direction une droite vectorielle ${\displaystyle {\overrightarrow {D}}}$) et de rapport non nul ; ce sont les applications affines de partie linéaire une dilatation vectorielle, sauf dans le cas du rapport 1.

Étant donnés deux points ${\displaystyle A}$, ${\displaystyle A'}$ et un hyperplan ${\displaystyle H}$ non parallèle à la droite ${\displaystyle (AA')}$, il existe une unique dilatation de base ${\displaystyle H}$ envoyant ${\displaystyle A}$ sur ${\displaystyle A'}$ ; on obtient l'image ${\displaystyle M'}$ d'un point ${\displaystyle M}$ par la construction :

En dimension finie, et si le corps de base a au moins 3 éléments, le groupe affine ${\displaystyle GA(E)}$ est engendré par les dilatations^[5],[4],[1].

Dilatation en géométrie projective

Si l'on plonge l'espace affine ${\displaystyle E}$ dans son complété projectif^[8], en lui adjoignant un hyperplan à l'infini ${\displaystyle H'}$, on sait que l'on peut munir le complémentaire ${\displaystyle E'}$ de l'hyperplan ${\displaystyle H}$ d'une structure d'espace affine (les droites qui sont sécantes en un point de ${\displaystyle H}$ dans ${\displaystyle E}$ deviennent parallèles dans ${\displaystyle E'}$ et celles qui sont parallèles dans ${\displaystyle E}$ deviennent sécantes en un point de ${\displaystyle H'}$).

À toute dilatation d'hyperplan ${\displaystyle H}$ de ${\displaystyle E}$ est alors associée une application affine de ${\displaystyle E'}$ qui n'est autre qu'une homothétie.

Et si on envoie un autre hyperplan que ${\displaystyle H}$ et ${\displaystyle H'}$ à l'infini, la dilatation devient une homologie non spéciale.

En résumé, il y a, en géométrie projective, identité entre les homothéties, les dilatations, et les homologies non spéciales^[9],[1].

• 
  Par complétion projective, cette dilatation...
• 
  ... devient une homothétie,...
• 
  ... ou une homologie non spéciale.

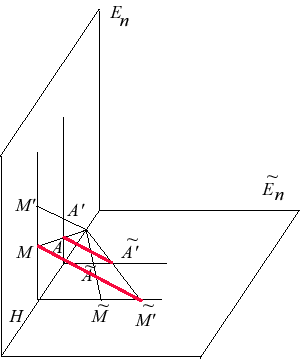
Réalisation d'une dilatation par projection

On plonge l'espace euclidien ${\displaystyle E_{n}\,}$de dimension ${\displaystyle n}$ comme hyperplan d'un espace ${\displaystyle E_{n+1}}$ de dimension ${\displaystyle n+1}$ et on fait tourner ${\displaystyle E_{n}\,}$ autour d'un hyperplan ${\displaystyle H\,}$(qui est de dimension ${\displaystyle n+1-2}$), de façon à en obtenir une copie ${\displaystyle {\tilde {E}}_{n}\,}$.

Tout point ${\displaystyle M\,}$ de ${\displaystyle E_{n}\,}$ a une copie ${\displaystyle {\tilde {M}}}$ dans ${\displaystyle {\tilde {E}}_{n}\,}$, donc aussi l'image ${\displaystyle M'\,}$ de ${\displaystyle M\,}$ par une dilatation de base ${\displaystyle H\,}$.

On montre que la droite ${\displaystyle (M{\tilde {M}}')}$ garde une direction fixe ${\displaystyle {\overrightarrow {D}}}$, ce qui montre que ${\displaystyle {\tilde {M}}'}$ s'obtient par projection de ${\displaystyle M\,}$ dans ${\displaystyle E_{n+1}\,}$ (projection de base ${\displaystyle {\tilde {E}}_{n}\,}$ et de direction ${\displaystyle {\overrightarrow {D}}}$). Connaissant ${\displaystyle {\tilde {M}}'}$, on en déduit ${\displaystyle M'\,}$par rotation^[10].

Autre acception de la notion de dilatation

Certains auteurs désignent par "dilatation" d'un plan affine^[11] ou même d'un espace affine^{[1],[12],[13]} une bijection affine transformant une droite en une droite parallèle, ou, ce qui est équivalent, une bijection affine laissant invariant point par point l'hyperplan de l'infini^[14]. Ceci caractérise les homothéties et les translations. Les auteurs prenant cette définition des dilatations, parlent d'affinité hyperplane pour la notion développée ci-dessus, et les auteurs prenant la définition ci-dessus des dilatations parlent d'homothétie-translation pour les homothéties ou translations.