Liukumoduuli

Liukumoduuli eli liukukerroin (engl. shear modulus^[1], tunnus G, joskus S tai μ) on materiaalifysiikassa suure, joka kuvaa materiaalin kykyä vastustaa leikkausjännityksen aiheuttamaa muodonmuutosta. Materiaalin liukumoduuli määritellään siitä koostuvaan kappaleeseen kohdistuvan leikkausjännityksen suhteena sen aiheuttamaan venymään.^[2]

${\displaystyle G\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\tau _{xy}}{\gamma _{xy}}}={\frac {F/A}{\Delta x/l}}={\frac {Fl}{A\Delta x}}}$

Leikkausjännitys

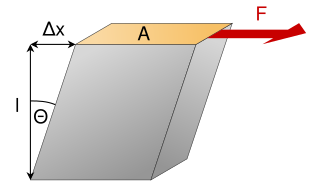
missä

${\displaystyle \tau _{xy}=F/A\,}$ = liukujännitys

${\displaystyle F}$ on vaikuttava voima

${\displaystyle A}$ on pinta-ala, johon voima kohdistuu

${\displaystyle \gamma _{xy}}$ = liukuvenymä. Insinöörialoilla ${\displaystyle$ :=\Delta x/l=\tan \theta } , muutoin ${\displaystyle$ :=\theta }

${\displaystyle \Delta x}$ poikittainen siirtymä

${\displaystyle l}$ on alkupeärinen pituus^[3]

SI-järjestelmässä liukumoduulin yksikkö on sama kuin paineen, pascal (Pa), mutta suuruusluokkansa vuoksi se ilmoitetaan yleensä gigapascaleina (GPa) tai Yhdysvalloissa usein paunoina neliötuumaa kohti. Sen dimensio on M¹L⁻¹T⁻², missä voima on korvattu massan ja kiihtyvyyden tulolla.

Merkitys

Materiaali	Liukumoduulinen tyypillinen arvo (GPa) (huoneenlämmössä)
Timantti[4]	478,0
Volframi[5]	158
Rakenneteräs	75
Rauta[5]	80
Platina[5]	61
Kupari[5]	45
Titaani[5]	41
Pii[5]	34
Kalustelasi[5]	16..35
Kvartsilasi[5]	31
Germanium[6]
Kulta[5]	27
Alumiini[5]	26
Pleksilasi[5]	1,2
Polyetyleeni[7]	0.117
Kumi[8]	0.0006

Liukumoduuli on yksi materiaalin jäykkyyttä kuvaavista suureista. Ne kaikki perustuvat yleistettyyn Hooken lakiin:

• Youngin moduuli E kuvaa materiaalin venymistä sitä venyttävän voiman tai puristumista sitä puristavan voiman suunnassa, esimerkiksi vedettäessä lankaa sen kummastakin päästä tai asetettaessa paino pylvään päälle,
• Poissonin suhde ν on pitkittäisessä ja poikittaisessa suunnassa tapahtuvien läpimitan muutosten suhde (venytettävä lanka ohenee ja puristuva pylväs paksunee)
• Puristusmoduuli K kuvaa sitä, miten kappale reagoi siihen kaikista suunnista kohdistuvaan hydrostaattiseen paineeseen, esimerkiksi veden alla meressä tai syvässä altaassa
• Liukumoduuli G kuvaa sitä, miten kappale reagoi leikkausjännitykseen, esimerkiksi leikattaessa sitä tylsillä saksilla.

Nämä moduulit eivät ole toisistaan riippumattomia, vaan isotrooppisilla aineilla niiden välillä vallitsevat yhteydet:^[9]

${\displaystyle K={\frac {E}{3(1-2\nu )}}}$ ja

${\displaystyle G={\frac {E}{2(1+\nu )}}}$ eli

${\displaystyle 2G(1+\nu )=E=3K(1-2\nu )}$

Liukumoduuli siis kuvaa sitä, miten kappaleen muoto muuttuu, kun siihen kohdistuu sen pinnan suuntainen voima samalla kun sen vastakkaiseen pintaan kohdistuu liikettä vastustava voima, esimerkiksi kitka. Jos kappale on suorakulmaisen särmiön muotoinen, se muuttuu tällaisen voiman vaikutuksesta suuntaissärmiöksi. Tämä muodonmuutos on sitä suurempi, mitä pienempi on materiaalin liukumoduuli. Anistrooppisisten materiaalien kuten puun ja paperin sekä myös yksittäisten kiteiden ominaisuudet eivät ole kaikissa suunnissa samat, ja niinpä mainitunlaisen voiman aikaansaaman muodonmuutoksen suuruuskin riippuu siitä, mihin pintaan voima kohdistuu. Tällaisiin materiaaleihin voidaan soveltaa Hooken lain yleistettyä muotoa, jossa liukumoduuli ja muut kimmoisuuskertoimet eivät enää ole yhdellä luvulla esitettäviä skalaarisuureita vaan ne korvataan materiaalin ominaisuuksia eri suunnissa kuvaavilla tensoreilla.

Fluidi voitaisiin määritellä aineeksi, jonka liukumoduuli on nolla.

Leikkausaallot

Homogeenisissa ja isotrooppisissa kiinteissä aineissa esiintyy kahdenalaisia aaltoja, pitkittäisiä paineaaltoja ja poikittaisia leikkausaaltoja. Poikittaisen aallon nopeus, ${\displaystyle (v_{s})}$ riippuu materiaalin liukumoduulista,

${\displaystyle v_{s}={\sqrt {\frac {G}{\rho }}}}$

missä

G on materiaalin liukumoduuli ja

${\displaystyle \rho }$ sen tiheys.^[9]

Metallien liukumoduulit

Kuparin liukumoduuli lämpötilan funktiona. Kokeelliset mittaustulokset^[10][11] esitetty värillisillä merkeillä.

Useimpien metallien liukumoduuli on suuruudeltaan noin 0,4 kertaa metallin kimmomoduuli.^[12] Metallien liukumoduulien on havaittu yleensä pienenevän lämpötilan kohotessa. Suuren paineen alaisena liukumoduuli näyttää lisäksi kasvavan paineen kasvavansa. Eri metallien liukumoduulien on lisäksi havaittu korreloivan niiden sulamispisteiden ja vakanssinmuodostusenergioiden kanssa.^[13]

On kehitetty useita malleja, joilla voidaan ennustaa metallien ja mahdollisesti metalliseostenkin liukumoduulit ja niiden riippuvuus lämpötilasta ja paineesta. Sellaisia ovat esimerkiksi:

1. MTS-liukumoduulimalli, jonka kehitti Y. Varshni vuonna 1970^[14] ja jota käytetään yhdessä plastisia virtauksia koskevan mekaanisen kynnysjännitysmallin (engl. Mechanical Threshold Stress, MTS) kanssa.^[15][16]
2. Steinbergin-Cochranin-Guinanin (SCG) liukumoduulimalli^[17], jota käytetään yhdessä Steinbergin-Cochranin-Guinanin-Lundin virtajännitysmallin kanssa.
3. Nadalin ja LePoacin (NP) liukumoduulimalli^[11], joka käyttää Frederick Lindmannin teoriaa liukumoduulin lämpötilariippuvuuden ja CSG-mallia sen paineriippuvuuden määrittämiseksi.

MTS-malli

MTS-liukumoduulimallin mukaan materiaalin liukumoduuli lämpötilassa T on

${\displaystyle \mu (T)=\mu _{0}-{\frac {D}{\exp(T_{0}/T)-1}}}$

missä ${\displaystyle \mu _{0}}$ on sen liukumoduuli absoluutisessa nollapisteessä (${\displaystyle T=0K}$), ja ${\displaystyle D}$ ja ${\displaystyle T_{0}}$ ovat kullekin materiaalille ominaisia vakioita.

SCG-malli

Steinbergin-Cocranin-Guinanin (SCG) mallin mukaan materiaalin liukumoduuli riippuu myös paineesta ja on

${\displaystyle \mu (p,T)=\mu _{0}+{\frac {\partial \mu }{\partial p}}{\frac {p}{\eta ^{\frac {1}{3}}}}+{\frac {\partial \mu }{\partial T}}(T-300);\quad \eta$ :={\frac {\rho }{\rho _{0}}}}

missä, μ₀ on sen liukumoduuli 300 kelvinin lämpötilassa paineen ollessa nolla ja kun sen tiheys on normaalin suuruinen eli η = 1.

NP-malli

Nadalin-LE Poacin (NP) liukumoduulimalli on kehitetty SCG-mallista. SCG-mallissa käytetty liukumoduulin empiirinen lämpötilariippuvuus on korvattu yhtälöllä, joka perustuu Lindemannin sulamisteoriaan. NP-mallin mukaan materiaalin liukumoduuli on:

${\displaystyle \mu (p,T)={\frac {1}{{\mathcal {J}}\left({\hat {T}}\right)}}\left[\left(\mu _{0}+{\frac {\partial \mu }{\partial p}}{\frac {p}{\eta ^{\frac {1}{3}}}}\right)\left(1-{\hat {T}}\right)+{\frac {\rho }{Cm}}~T\right];\quad C:={\frac {\left(6\pi ^{2}\right)^{\frac {2}{3}}}{3}}f^{2}}$

missä

${\displaystyle {\mathcal {J}}({\hat {T}}):=1+\exp \left[-{\frac {1+1/\zeta }{1+\zeta /\left(1-{\hat {T}}\right)}}\right]\quad {\text{kun}}\quad {\hat {T}}:={\frac {T}{T_{m}}}\in [0,1+\zeta ],}$

missä μ₀ on liukumoduuli absoluuttisessa nollapisteessä ja valitussa paineessa, ζ on materiaalista riippuva parametri, m atomimassa ja f Lindemannin vakio.

Liukurelaksaatiomoduuli

Liukurelaksaatiomoduuli ${\displaystyle G(t)}$ on liukumoduulin ajasta riippuva yleistys^[18]:

${\displaystyle G=\lim _{t\to \infty }G(t)}$.

Katso myös

• Elastinen kerroin
• Poissonin suhde

Lähteet

1. Tapio Salmi, Sami Pajunen: ”Suomalais-englantilainen sanasto”, Lujuusoppi, s. 460. Pressus, 2010. ISBN 978-952-983567-6
2. Alan D. McNaught, Andrew Wilkinson: ”Shear modulis, G”, Compendium of Chemical Terminology, 2. ed. ("Gold Book"). IUPAC. ISBN 0-86542-684-8Doi = 10.1351/goldbook.S05635 Teoksen verkkoversio.
3. Hannu Peltonen: ”Leikkausjännitys”, Insinöörin (AMK) fysiikka, osa I, s. 148. Lahden Teho-opetus Oy, 2005. ISBN 952-5191-17-6
4. H. J. McSkimin, P. Andreatch: P. cite journal. J. Appl. Phys., 1972, 43. vsk, nro 7, s. 2944–2948. doi:10.1063/1.1661636 Bibcode:1972JAP....43.2944M
5. Esko Valtanen: ”Kimmokerroin, liukukerroin, puristuvuuskerroin ja Poissonin luku”, Matemaattisia kaavoja ja taulukoita, s. 405–406. Genesis-kirjat, 2013. ISBN 978-952-9867-37-0
6. Hannu Peltonen, Juha Perkkiö, Kari Vierinen: ”Kiinteiden aineiden ominaisuuksia”, Insinöörin (AMK) fysiikka, osa II, s. 468. Lahden teho-opetus, 2012. ISBN 978-952-519123-3
7. Crandall, Dahl, Lardner: An Introduction to the Mechanics of Solids. Boston: McGraw-Hill, 1959. ISBN 0-07-013441-3
8. Pete Spance: Cure system effect on low temperature dynamic shear modulus of natural rubber. Rubber World, 1973. Artikkelin verkkoversio.
9. Hannu Peltonen, Juha Perkkiö, Kari Vierinen: ”Kiinteiden aineiden ominaisuuksia”, Insinöörin (AMK) fysiikka, osa II, s. 92. Lahden teho-opetus, 2012. ISBN 978-952-519123-3
10. W. Overton, John Gaffney: Temperature Variation of the Elastic COnstants of Cubic Elements. I. Copper.. Physical Review, 1955, 98. vsk, nro 4, s. 969. doi:10.1103/PhysRev.98.969 Bibcode:1955PhRv...98..969O
11. Marie-Hélène Nadal, Philippe LePoac: Continuous model for the shear modulus as a function of pressure and temperature up to the melting point: Analysis and ultrasonic validation. Journal of Applied Physics, 2003, 93. vsk, nro 5. doi:10.1063/1.1539913 Bibcode:2003JAP....93.2472N
12. ”Kimmoisuus”, Iso tietosanakirja, 6. osa (Kansallishenki–Kouko), s. 787. Otava, 1933.
13. N. H. March: Electron Correlation in Molecules and Condensed Phases, s. 363. Springer, 1996. ISBN 0-306-44844-0 Teoksen verkkoversio.
14. Y. Varshi: Temperature Dependence of the Elastic Constants. Physical Review B, 1970, 2. vsk, nro 10, s. 3952–3958. doi:10.1103/PhysRevB.2.3952 Bibcode:1970PhRvB...2.3952V
15. Shuh Rong Chen, George T. Gray: Constitutive behavior of tantalum and tantalum-tungsten alloys Metallurgical and Materials Transactions A. doi:10.1007/BF02663849 Bibcode:1996MMTA...27.2994C
16. D. M. Goto, R. K. Garrett, J. F. Bingert, S. R. Chen, G. T. Gray: The mechanical treshold stress constitutive-strength model description of HY-100 steel. Metallurgical and Materials Transactions A, 2000, 31. vsk, nro 8, s. 1985–1996. doi:10.1007/s11661-000-0226-8 Artikkelin verkkoversio. (Arkistoitu – Internet Archive)
17. M. Guinan, D: Steinberg: Pressure and temperature derivatives of the isotropic polycrystalline shear modulus for 65 elements. Journal of Physics and Chemistry of Solids, 1974, 35. vsk, nro 11. doi:doi=10.1016/S0022-3697(74)80278-7 Bibcode:1974JPCS...35.1501G
18. Michael Rubinstein: Polymer physics, s. 284. Oxford: Oxford University Press, 2003. ISBN 019852059X OCLC:50339757

Käännös suomeksi

Tämä artikkeli tai sen osa on käännetty tai siihen on haettu tietoja muunkielisen Wikipedian artikkelista.
Alkuperäinen artikkeli: en:Shear modulus