Grupo modular

En matemáticas, el grupo modular es el grupo lineal especial proyectivo $PSL(2, Z)$ de matrices de orden 2 × 2 con coeficientes enteros y determinante 1. Las matrices $A$ y $- A$ se identifican entre sí. El grupo modular actúa en la mitad superior del plano complejo mediante transformaciones lineales fraccionarias. El nombre "grupo modular" proviene de su relación con los espacios modulares y no guarda relación con la aritmética modular.

El grupo modular $Γ$ es el grupo de transformaciones fraccionales lineales de la mitad superior del plano complejo, que tienen la forma

z\mapsto {\frac {az+b}{cz+d}},

donde $a$ , $b$ , $c$ , $d$ son números enteros y $ad - bc = 1$ . La operación de grupo es una función compuesta.

Este grupo de transformaciones es isomorfo al grupo lineal especial proyectivo $PSL(2, Z)$ , que es el cociente del grupo lineal especial bidimensional $SL(2, Z)$ sobre los enteros por su centro ${I, - I}$ . En otras palabras, $PSL(2, Z)$ consta de todas las matrices

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}

donde $a$ , $b$ , $c$ , $d$ son números enteros, $ad - bc = 1$ y los pares de matrices $A$ y $- A$ se consideran idénticos. La operación del grupo es la multiplicación de matrices habitual.

Algunos autores definen el grupo modular como $PSL(2, Z)$ , y otros lo definen como el grupo más grande de $SL(2, Z)$ .

Algunas relaciones matemáticas requieren la consideración del grupo $GL(2, Z)$ de matrices con determinante más o menos uno ( $SL(2, Z)$ es un subgrupo de este grupo). De manera similar, $PGL(2, Z)$ es el grupo de cocientes $GL(2, Z)/{I, - I}$ . Una matriz 2 × 2 con determinante unitario es una matriz simpléctica y, por tanto, $SL(2, Z) = Sp(2, Z)$ , el grupo simpléctico de las matrices de orden 2 × 2.

Determinación de sus elementos

Para encontrar explícitamente una matriz

${\begin{pmatrix}a&x\\b&y\end{pmatrix}}$

en $SL(2, Z)$ , se comienza con dos enteros coprimos $a,b$ y se resuelve la ecuación del determinante

$ay-bx=1.$

(obsérvese que la ecuación del determinante obliga a $a,b$ a ser coprimos, ya que de lo contrario habría un factor $c$ tal que $ca'=a$ , $cb'=b$ , y por lo tanto,

$c(a'y-b'x)=1$

no tendría soluciones enteras). Por ejemplo, si $a=7,{\text{ }}b=6$ entonces la ecuación del determinante implica que

$7y-6x=1$

y tomando $y=-5$ y $x=-6$ da $-35-(-36)=1$ , por lo tanto,

${\begin{pmatrix}7&-6\\6&-5\end{pmatrix}}$

es una matriz buscada. Entonces, usando la proyección, estas matrices definen elementos en $PSL(2, Z)$ .

El determinante unidad de

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}

implica que las fracciones _{$a / b$}, _{$a / c$}, _{$c / d$}, _{$b / d$} son todas irreducibles, es decir, no tienen factores comunes (siempre que los denominadores sean distintos de cero, por supuesto). De manera más general, si $p / q$ es una fracción irreducible, entonces

{\frac {ap+bq}{cp+dq}}

también es irreducible (de nuevo, siempre que el denominador sea distinto de cero). Cualquier par de fracciones irreducibles se puede conectar de esta manera; es decir, para cualquier par $p / q$ y $r / s$ de fracciones irreducibles, existen elementos

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \operatorname {SL} (2,\mathbf {Z} )

tal que

r=ap+bq\quad {\mbox{ y }}\quad s=cp+dq.

Los elementos del grupo modular proporcionan una simetría en la retícula bidimensional. Sean $ω 1$ y $ω 2$ dos números complejos cuya razón no es real. Entonces el conjunto de puntos

\Lambda (\omega _{1},\omega _{2})=\{m\omega _{1}+n\omega _{2}:m,n\in \mathbf {Z} \}

es una red de paralelogramos en el plano. Un par diferente de vectores $α 1$ y $α 2$ generarán exactamente el mismo entramado si y solo si

{\begin{pmatrix}\alpha _{1}\\\alpha _{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}\omega _{1}\\\omega _{2}\end{pmatrix}}

para alguna matriz en $GL(2, Z)$ . Es por esta razón que una función doblemente periódica, como la función elíptica, poseen una simetría de grupo modular.

La acción del grupo modular sobre los números racionales se puede entender más fácilmente imaginando una retícula cuadrada, con el punto $(p, q)$ correspondiente a la fracción $p / q$ (véase huerto de Euclides). Una fracción irreducible es aquella que es "visible" desde el origen; la acción del grupo modular sobre una fracción nunca lleva de un valor "visible" (irreducible) a uno "oculto" (reducible), y viceversa.

Téngase en cuenta que cualquier miembro del grupo modular aplica la recta real proyectada extendida uno a uno sobre sí misma, y además aplica biyectivamente la recta racional proyectada extendida (los racionales con el infinito) sobre sí misma, los irracionales sobre los irracionales, los trascendentes sobre los trascendentes, los números no reales sobre los números no reales, el semiplano superior sobre semiplano superior, etcétera.

Si $p n -1 / q n -1$ y $p n / q n$ son dos términos convergentes sucesivos de una fracción continua, entonces la matriz

{\begin{pmatrix}p_{n-1}&p_{n}\\q_{n-1}&q_{n}\end{pmatrix}}

pertenece a $GL(2, Z)$ . En particular, si $bc - ad = 1$ para enteros positivos $a$ , $b$ , $c$ , $d$ con $a < b$ y $c < d$ , entonces $a / b$ y $c / d$ serán elementos vecinos en la sucesión de Farey de orden $max(b, d)$ . Los casos especiales importantes de términos convergentes de fracciones continuas incluyen la sucesión de Fibonacci y las soluciones de la ecuación de Pell. En ambos casos, los números se pueden organizar para formar un subconjunto que forma un semigrupo del grupo modular.

Presentación

Se puede demostrar que el grupo modular es generado mediante las dos transformaciones

{\begin{aligned}S&:z\mapsto -{\frac {1}{z}}\\T&:z\mapsto z+1\end{aligned}}

de modo que cada elemento del grupo modular pueda ser representado (de manera no única) por la composición de potencias de $S$ y $T$ . Geométricamente, $S$ representa la inversión en el círculo unitario seguida de una reflexión con respecto al eje imaginario, mientras que $T$ representa una traslación unitaria hacia la derecha.

Los generadores $S$ y $T$ obedecen a las relaciones $S 2 = 1$ y $(ST) 3 = 1$ . Se puede demostrar^[1] que se trata de un conjunto completo de relaciones, por lo que el grupo modular tiene la presentación:

\Gamma \cong \left\langle S,T\mid S^{2}=I,\left(ST\right)^{3}=I\right\rangle

Esta presentación describe el grupo modular como el grupo triangular $D(2, 3, \infty)$ rotacional (infinito, ya que no hay relación en $T$ ) y, por lo tanto, se asigna a todos los grupos de triángulos $(2, 3, n)$ agregando la relación $T n = 1$ , que ocurre, por ejemplo, en un subgrupo de congruencia $Γ(n)$ .

Usando los generadores $S$ y $ST$ en lugar de $S$ y $T$ , se demuestra cómo el grupo modular es isomorfo al producto libre de grupos de los grupos cíclicos $C 2$ y $C 3$ :

\Gamma \cong C_{2}*C_{3}

Acción de $T : z \mapsto z + 1$ sobre $H$
Acción de $S : z \mapsto - 1 / z$ sobre $H$

Grupo de trenzas

Thumb — El grupo de trenzas $B 3$ es la extensión central universal del grupo modular

El grupo de trenzas $B 3$ es la extensión central universal del grupo modular, asentadas como retículas dentro del grupo de cobertura universal (topológico) $SL 2 (R) \to PSL 2 (R)$ . Además, el grupo modular tiene un centro trivial y, por lo tanto, el grupo modular es isomorfo al grupo cociente de $B 3$ módulo su centro; de manera equivalente, al grupo de automorfismos internos de $B 3$ .

El grupo de trenzas $B 3$ a su vez es isomorfo al nudo de trébol del grupo de nudos.

Cocientes

Los cocientes por subgrupos de congruencia son de gran interés.

Otros cocientes importantes son los grupos de triángulos $(2, 3, n)$ , que corresponden geométricamente a descender a un cilindro, realizando el cociente de la coordenada $x$ módulo $n$ , como $T n = (z \mapsto z + n)$ . $(2, 3, 5)$ es el grupo de simetría icosaedral, y el grupo triangular $(2, 3, 7)$ (y el teselado asociado) es un recubrimiento para todas las superficies de Hurwitz.

Presentando como un grupo matricial

El grupo ${\text{SL}}_{2}(\mathbb {Z} )$ puede ser generado por las dos matrices^[2]

S={\begin{pmatrix}0&-1\\1&0\end{pmatrix}},{\text{ }}T={\begin{pmatrix}1&1\\0&1\end{pmatrix}}

ya que

S^{2}=-I_{2},{\text{ }}(ST)^{3}={\begin{pmatrix}0&-1\\1&1\end{pmatrix}}^{3}=-I_{2}

La proyección ${\text{SL}}_{2}(\mathbb {Z} )\to {\text{PSL}}_{2}(\mathbb {Z} )$ convierte estas matrices en generadores de ${\text{PSL}}_{2}(\mathbb {Z} )$ , con relaciones similares a la presentación de grupo.

Véase también: PSL2(R)

El grupo modular es importante porque forma un subgrupo del grupo de isometrías del plano hiperbólico. Si se considera el modelo del semiplano superior $H$ de la geometría del plano hiperbólico, entonces el grupo de todas las isometrías con preservación de la orientación de $H$ constan de todas las transformaciones de Möbius de la forma

z\mapsto {\frac {az+b}{cz+d}}

donde $a$ , $b$ , $c$ , $d$ son números reales. En términos de coordenadas homogéneas, el grupo $PSL(2, R)$ actúa en el semiplano superior $H$ por proyectividad:

[z,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\,=\,[az+b,\ cz+d]\,\thicksim \,\left[{\frac {az+b}{cz+d}},\ 1\right].

Esta acción es fiel. Dado que $PSL(2, Z)$ es un subgrupo de $PSL(2, R)$ , el grupo modular es un subgrupo del grupo de isometrías que preservan la orientación de $H$ .^[3]

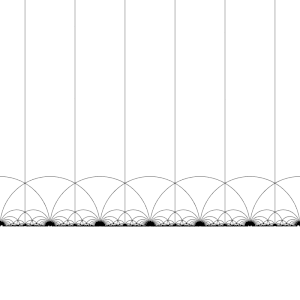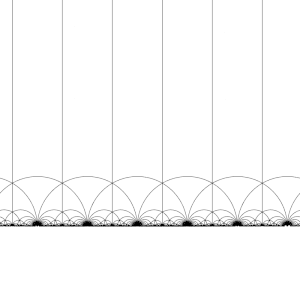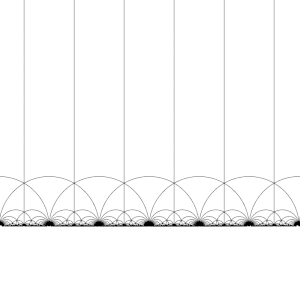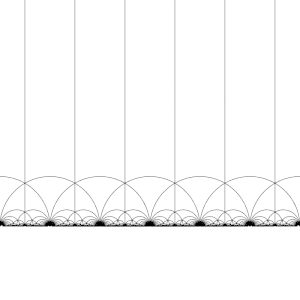
Teselación del plano hiperbólico

El grupo modular $Γ$ actúa sobre $H$ como un subgrupo discreto de $PSL(2, R)$ , es decir, para cada $z$ en $H$ se puede encontrar un entorno de $z$ que no contiene ningún otro elemento de la órbita de $z$ . Esto también significa que se puede construir el dominio fundamental, que (aproximadamente) contienen exactamente un representante de la órbita de cada $z$ en $H$ (los límites del dominio se deben elegir cuidadosamente).

Hay muchas formas de construir un dominio fundamental, pero una opción común es la región

R=\left\{z\in \mathbf {H} \colon \left|z\right|>1,\,\left|\,{\mbox{Re}}(z)\,\right|<{\tfrac {1}{2}}\right\}

delimitada por las rectas verticales $Re(z) = 1 / 2$ y $Re(z) = - 1 / 2$ , y el círculo $| z | = 1$ . Esta región es un triángulo hiperbólico. Tiene vértices en $1 / 2 + i \sqrt 3 / 2$ y $- 1 / 2 + i \sqrt 3 / 2$ , donde el ángulo entre sus lados es $π / 3$ , y un tercer vértice en el infinito, donde el ángulo entre sus lados es 0.

Al transformar esta región a su vez por cada uno de los elementos del grupo modular, se crea un teselado regular del plano hiperbólico mediante triángulos hiperbólicos congruentes conocido como teselado triangular de orden infinito V6.6.∞. Debe tenerse en cuenta que cada uno de estos triángulos tiene un vértice en el infinito o en el eje real $Im(z) = 0$ . Este teselado se puede extender al disco de Poincaré, donde cada triángulo hiperbólico tiene un vértice en el límite del disco. El teselado del disco de Poincaré viene dado de forma natural por el $J$ -invariante, que es invariante bajo el grupo modular, y alcanza cada número complejo una vez en cada triángulo de estas regiones.

Esta teselación se puede refinar ligeramente, dividiendo cada región en dos mitades (convencionalmente coloreadas en blanco y negro), agregando una aplicación de inversión de orientación; los colores corresponden entonces a la orientación del dominio. Al agregar $(x, y) \mapsto (- x, y)$ y tomar la mitad derecha de la región $R$ (donde $Re(z) \geq 0$ ) se obtiene la teselación habitual. Esta teselación apareció descrita por primera vez en (Klein, 1878/79a),^[4] donde se acredita a Richard Dedekind, en referencia a (Dedekind, 1877).^[4]^[5]

La aplicación de los grupos $(2, 3, \infty) \to (2, 3, n)$ (del grupo modular al grupo triangular) se puede visualizar en términos de este mosaico (produciendo un mosaico en la curva modular), como se muestra en la animación de la derecha.

Más información Teselados uniformes paracompactos en la familia [∞,3], Simetría: [∞,3], (*∞32) ...

Teselados uniformes paracompactos en la familia [∞,3]
Simetría: [∞,3], (*∞32)							[∞,3]⁺ (∞32)	[1⁺,∞,3] (*∞33)		[∞,3⁺] (3*∞)

		=	=	=				= or	= or	=

{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h₂{∞,3}	s{3,∞}
Duales uniformes


V∞³	V3.∞.∞	V(3.∞)²	V6.6.∞	V3^∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)³		V3.3.3.3.3.∞

Cerrar

Artículo principal: Subgrupo de congruencia

Los subgrupo importantes del grupo modular $Γ$ , llamados subgrupos de congruencia, se dan imponiendo una relación de congruencia en las matrices asociadas.

Existe un homomorfismo $SL(2, Z) \to SL(2, Z / N Z)$ natural que se obtiene al reducir las entradas mediante la operación módulo $N$ . Esto induce un homomorfismo en el grupo modular $PSL(2, Z) \to PSL(2, Z / N Z)$ . El núcleo de este homomorfismo se denomina subgrupo de congruencia principal del nivel $N$ , denotado $Γ(N)$ . Se tiene la siguiente sucesión exacta:

1\to \Gamma (N)\to \Gamma \to {\mbox{PSL}}(2,\mathbf {Z} /N\mathbf {Z} )\to 1

.

El núcleo del homomorfismo $Γ(N)$ es un subgrupo normal del grupo modular $Γ$ . El grupo $Γ(N)$ se da como el conjunto de todas las transformaciones modulares

z\mapsto {\frac {az+b}{cz+d}}

para las que $a \equiv d \equiv \pm1 (mod N)$ y $b \equiv c \equiv 0 (mod N)$ .

Es fácil demostrar que la traza de una matriz que representa un elemento de $Γ(N)$ no puede ser -1, 0 o 1, por lo que estos subgrupos son torsiones (existen otros subgrupos sin torsión).

El principal subgrupo de congruencia del nivel 2, $Γ(2)$ , también se denomina grupo modular $Λ$ . Dado que $PSL(2, Z /2 Z)$ es isomorfo al $S 3$ , $Λ$ es un subgrupo de índice 6. El grupo $Λ$ consta de todas las transformaciones modulares para las que $a$ y $d$ son impares y $b$ y $c$ son pares.

Otra familia importante de subgrupos de congruencia son los grupos modulares $Γ 0 (N)$ definidos como el conjunto de todas las transformaciones modulares para las que $c \equiv 0 (mod N)$ , o de manera equivalente, como el subgrupo cuyas matrices se convierten a la forma triangular superior según el módulo de reducción $N$ . Se debe tener en cuenta que $Γ(N)$ es un subgrupo de $Γ 0 (N)$ . Las curvas modulares asociadas con estos grupos son un aspecto de monstrous moonshine -para un número primo $p$ , la curva modular del normalizador es de genus cero si y solo si $p$ divide el orden del grupo monstruo, o de manera equivalente, si $p$ es un primo supersingular.

Un subconjunto importante del grupo modular es el monoide diádico, que es el monoide de todas las cadenas de la forma $ST k ST m ST n ...$ para enteros positivos $k, m, n,...$ . Este monoide aparece naturalmente en el estudio de curvas fractales y describe las simetrías de la autosimilitud de la función de Cantor, de la función del signo de interrogación de Minkowski y del copo de nieve de Koch, siendo cada una un caso especial de la curva de De Rham general. El monoide también tiene representaciones lineales de dimensiones superiores. Por ejemplo, se puede entender que la representación $N = 3$ describe la auto-simetría de la curva del manjar blanco.

El grupo $GL(2, Z)$ coincide con las transformaciones lineales que conservan la retícula estándar $Z 2$ , y $SL(2, Z)$ son las transformaciones que conservan la orientación y preservan esta retícula; así descienden a auto homeomorfismos del toro (tranformación SL a sistemas que preservan la orientación), y de hecho aplican isomórficamente al grupo de clases de aplicación (extendido) del toro, lo que significa que cada auto-homeomorfismo del toro es isotópico a una aplicación de esta forma. Las propiedades algebraicas de una matriz como elemento de $GL(2, Z)$ corresponden a la dinámica de las transformaciones inducidas en el toro.

El grupo modular se puede generalizar a los grupos de Hecke, denominados así en memoria de Erich Hecke, y definidos de la siguiente manera.^[7]

El grupo de Hecke $H q$ con $q \geq 3$ , es el grupo discreto generado por

{\begin{aligned}z&\mapsto -{\frac {1}{z}}\\z&\mapsto z+\lambda _{q},\end{aligned}}

donde $λ q = 2 cos π / q$ . Para valores pequeños de $q \geq 3$ , se tiene que:

{\begin{aligned}\lambda _{3}&=1,\\\lambda _{4}&={\sqrt {2}},\\\lambda _{5}&={\frac {1+{\sqrt {5}}}{2}},\\\lambda _{6}&={\sqrt {3}},\\\lambda _{8}&={\sqrt {2+{\sqrt {2}}}}.\end{aligned}}

El grupo modular $Γ$ es isomorfo a $H 3$ y comparten propiedades y aplicaciones, por ejemplo, posee el producto libre de los grupos cíclicos.

\Gamma \cong C_{2}*C_{3},

más generalmente se tiene que

H_{q}\cong C_{2}*C_{q},

que corresponde al grupo triangular $(2, q, \infty)$ . De manera similar, existe una noción de subgrupos de congruencia principal asociada a los ideales principales en $Z [λ]$ .

El grupo modular y sus subgrupos fueron estudiados en detalle por primera vez por Richard Dedekind y por Felix Klein como parte de su Programa de Erlangen en la década de 1870. Sin embargo, las funciones elípticas estrechamente relacionadas fueron estudiados por Joseph-Louis Lagrange en 1785, y Carl Gustav Jakob Jacobi y Niels Henrik Abel publicaron más resultados sobre funciones elípticas en 1827.

[1]
Alperin, Roger C. (April 1993). « $PSL 2 (Z) = Z 2 * Z 3$ ». Amer. Math. Monthly 100 (4): 385-386. JSTOR 2324963. doi:10.2307/2324963.
[2]
Conrad, Keith. «SL(2,Z)».
[3]
McCreary, Paul R.; Murphy, Teri Jo; Carter, Christian. «The Modular Group». The Mathematica Journal 9 (3). Archivado desde el original el 11 de agosto de 2019. Consultado el 3 de enero de 2022.
[4]
Le Bruyn, Lieven (22 de abril de 2008), Dedekind or Klein?.
[5]
Stillwell, John (January 2001). «Modular Miracles». The American Mathematical Monthly 108 (1): 70-76. ISSN 0002-9890. JSTOR 2695682. doi:10.2307/2695682.
[6]
Westendorp, Gerard. «Platonic tessellations of Riemann surfaces». www.xs4all.nl.
[7]
Rosenberger, Gerhard; Fine, Benjamin; Gaglione, Anthony M.; Spellman, Dennis. Combinatorial Group Theory, Discrete Groups, and Number Theory. p. 65.

Apostol, Tom M. (1990). Modular Functions and Dirichlet Series in Number Theory (2nd edición). New York: Springer. ch. 2. ISBN 0-387-97127-0.
Klein, Felix (1878–1879), «Über die Transformation der elliptischen Funktionen und die Auflösung der Gleichungen fünften Grades (On the transformation of elliptic functions and ...)», Math. Annalen 14: 13-75, doi:10.1007/BF02297507, archivado desde el original el 19 de julio de 2011, consultado el 3 de junio de 2010.
Dedekind, Richard (September 1877), «Schreiben an Herrn Borchardt über die Theorie der elliptische Modul-Functionen», Crelle's Journal 83: 265-292..

Datos: Q1834342

[1] [1]
Alperin, Roger C. (April 1993). « $PSL 2 (Z) = Z 2 * Z 3$ ». Amer. Math. Monthly 100 (4): 385-386. JSTOR 2324963. doi:10.2307/2324963.

[2] [2]
Conrad, Keith. «SL(2,Z)».

[3] [3]
McCreary, Paul R.; Murphy, Teri Jo; Carter, Christian. «The Modular Group». The Mathematica Journal 9 (3). Archivado desde el original el 11 de agosto de 2019. Consultado el 3 de enero de 2022.

[lebruyn-4] [4]
Le Bruyn, Lieven (22 de abril de 2008), Dedekind or Klein?.

[5] [5]
Stillwell, John (January 2001). «Modular Miracles». The American Mathematical Monthly 108 (1): 70-76. ISSN 0002-9890. JSTOR 2695682. doi:10.2307/2695682.

[westendorp-6] [6]
Westendorp, Gerard. «Platonic tessellations of Riemann surfaces». www.xs4all.nl.

[7] [7]
Rosenberger, Gerhard; Fine, Benjamin; Gaglione, Anthony M.; Spellman, Dennis. Combinatorial Group Theory, Discrete Groups, and Number Theory. p. 65.

[1]

[2]

[3]

[4]

[5]

[6]

[7]