Square

This article is about the shape. For other uses, see Square (disambiguation).

In geometry, a square is a regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal sides. As with all rectangles, a square's angles are right angles (90 degrees, or π/2 radians), making adjacent sides perpendicular. The area of a square is the side length multiplied by itself, and so in algebra, multiplying a number by itself is called squaring.

Square
Type	quadrilateral regular polygon hypercube cross-polytope
Edges and vertices	4
Symmetry group	order-8 dihedral
Area	side2
Internal angle (degrees)	π/2 (90°)
Perimeter	4 · side

Equal squares can tile the plane edge-to-edge in the square tiling. Square tilings are ubiquitous in tiled floors and walls, graph paper, image pixels, and game boards. Square shapes are also often seen in building floor plans, origami paper, food servings, in graphic design and heraldry, and in instant photos and fine art.

The formula for the area of a square forms the basis of the calculation of area and motivates the search for methods for squaring the circle by compass and straightedge, now known to be impossible. Squares can be inscribed in any smooth or convex curve such as a circle or triangle, but it remains unsolved whether a square can be inscribed in every simple closed curve. Several problems of squaring the square involve subdividing squares into unequal squares. Mathematicians have also studied packing squares as tightly as possible into other shapes.

Squares can be constructed by straightedge and compass, through their Cartesian coordinates, or by repeated multiplication by ${\displaystyle i}$ in the complex plane. They form the metric balls for taxicab geometry and Chebyshev distance, two forms of non-Euclidean geometry. Although spherical geometry and hyperbolic geometry both lack polygons with four equal sides and right angles, they have square-like regular polygons with four sides and other angles, or with right angles and different numbers of sides.

Definitions and characterizations

Among rectangles (top row), the square is the shape with equal sides (blue, middle). Among rhombuses (bottom row), the square is the shape with right angles (blue, middle).

Squares can be defined or characterized in many equivalent ways. If a polygon in the Euclidean plane satisfies any one of the following criteria, it satisfies all of them:

• A square is a polygon with four equal sides and four right angles; that is, it is a quadrilateral that is both a rhombus and a rectangle^[1]
• A square is a rectangle with four equal sides.^[1]
• A square is a rhombus with a right angle between a pair of adjacent sides.^[1]
• A square is a rhombus with all angles equal.^[1]
• A square is a parallelogram with one right angle and two adjacent equal sides.^[1]
• A square is a quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other. That is, it is a rhombus with equal diagonals.^[2]
• A square is a quadrilateral with successive sides ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$, ${\displaystyle d}$ whose area is^[3] $${\displaystyle A={\frac {1}{4}}(a^{2}+b^{2}+c^{2}+d^{2}).}$$

Squares are the only regular polygons whose internal angle, central angle, and external angle are all equal (they are all right angles).^[4]

Properties

A square is a special case of a rhombus (equal sides, opposite equal angles), a kite (two pairs of adjacent equal sides), a trapezoid (one pair of opposite sides parallel), a parallelogram (all opposite sides parallel), a quadrilateral or tetragon (four-sided polygon), and a rectangle (opposite sides equal, right-angles),^[1] and therefore has all the properties of all these shapes, namely:

• All four internal angles of a square are equal (each being 90°, a right angle).^[4][5]
• The central angle of a square is equal to 90°.^[4]
• The external angle of a square is equal to 90°.^[4]
• The diagonals of a square are equal and bisect each other, meeting at 90°.^[5]
• The diagonals of a square bisect its internal angles, forming adjacent angles of 45°.^[6]
• All four sides of a square are equal.^[7]
• Opposite sides of a square are parallel.^[8]

All squares are similar to each other, meaning they have the same shape.^[9] One parameter (typically the length of a side or diagonal)^[10] suffices to specify a square's size. Squares of the same size are congruent.^[11]

Measurement

The area of a square is the product of the lengths of its sides.

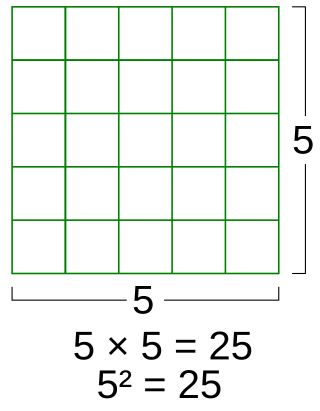
A square whose four sides have length ${\displaystyle \ell }$ has perimeter^[12] ${\displaystyle P=4\ell }$ and diagonal length ${\displaystyle d={\sqrt {2}}\ell }$.^[13] (The square root of 2, appearing in this formula, is irrational, meaning that it is not the ratio of any two integers. It is approximately equal to 1.414.^[14]) A square's area is^[13] $${\displaystyle A=\ell ^{2}={\tfrac {1}{2}}d^{2}.}$$ This formula for the area of a square as the second power of its side length led to the use of the term squaring to mean raising any number to the second power.^[15] Reversing this relation, the side length of a square of a given area is the square root of the area. Squaring an integer, or taking the area of a square with integer sides, results in a square number; these are figurate numbers representing the numbers of points that can be arranged into a square grid.^[16]

Since four squared equals sixteen, a four by four square has an area equal to its perimeter. That is, it is an equable shape. The only other equable integer rectangle is a three by six rectangle.^[17]

Because it is a regular polygon, a square is the quadrilateral of least perimeter enclosing a given area. Dually, a square is the quadrilateral containing the largest area within a given perimeter.^[18] Indeed, if A and P are the area and perimeter enclosed by a quadrilateral, then the following isoperimetric inequality holds: $${\displaystyle 16A\leq P^{2}}$$ with equality if and only if the quadrilateral is a square.^[19][20]

Symmetry

Main article: Symmetry group of a square

The square is the most symmetrical of the quadrilaterals.^[21] Eight rigid transformations of the plane take the square to itself:^[22]

The square's initial position
(the identity transformation)

Rotation by 90° anticlockwise

Rotation by 180°

Rotation by 270°

Diagonal NW–SE reflection

Horizontal reflection

Diagonal NE–SW reflection

Vertical reflection

The axes of reflection symmetry and centers of rotation symmetry of a square (top), rectangle and rhombus (center), isosceles trapezoid, kite, and parallelogram (bottom)

For an axis-parallel square centered at the origin, each symmetry acts by a combination of negating and swapping the Cartesian coordinates of points.^[23] The symmetries permute the eight isosceles triangles between the half-edges and the square's center (which stays in place); any of these triangles can be taken as the fundamental region of the transformations.^[24] Each two vertices, each two edges, and each two half-edges are mapped one to the other by at least one symmetry (exactly one for half-edges).^[21] All regular polygons also have these properties, which are expressed by saying that symmetries of a square and, more generally, a regular polygon act transitively on vertices and edges, and simply transitively on half-edges.

Combining any two of these transformations by performing one after the other continues to take the square to itself, and therefore produces another symmetry. Repeated rotation produces another rotation with the summed rotation angle. Two reflections with the same axis return to the identity transformation, while two reflections with different axes rotate the square. A rotation followed by a reflection, or vice versa, produces a different reflection. This composition operation gives the eight symmetries of a square the mathematical structure of a group, called the group of the square or the dihedral group of order eight.^[22] Other quadrilaterals, like the rectangle and rhombus, have only a subgroup of these symmetries.^[25][26]

Three-point perspective of a cube, showing perspective transformations of its six square faces into six different quadrilaterals

The shape of a square, but not its size, is preserved by similarities of the plane. Other kinds of transformations of the plane can take squares to other kinds of quadrilateral. An affine transformation can take a square to any parallelogram, or vice versa; a projective transformation can take a square to any quadrilateral, or vice versa. This implies that, when viewed in perspective, a square can look like any quadrilateral. A Möbius transformation can take the vertices of a square (but not its edges) to the vertices of a harmonic quadrilateral.^[27]

The wallpaper groups are symmetry groups of two-dimensional repeating patterns. For many of these groups the basic unit of repetition (the unit cell of its period lattice) can be a square, and for three of these groups, p4, p4m, and p4g, it must be a square.^[28]

p4, Egyptian tomb ceiling

p4m, Nineveh & Persia

p4g, China

Wallpaper groups of tilings from The Grammar of Ornament

Inscribed and circumscribed circles

The inscribed circle (purple) and circumscribed circle (red) of a square (black)

The inscribed circle of a square is the largest circle that can fit inside that square. Its center is the center point of the square, and its radius (the inradius of the square) is ${\displaystyle r=\ell /2}$. Because this circle touches all four sides of the square (at their midpoints), the square is a tangential quadrilateral. The circumscribed circle of a square passes through all four vertices, making the square a cyclic quadrilateral. Its radius, the circumradius, is ${\displaystyle R=\ell /{\sqrt {2}}}$.^[29] If the inscribed circle of a square ${\displaystyle ABCD}$ has tangency points ${\displaystyle E}$ on ${\displaystyle AB}$, ${\displaystyle F}$ on ${\displaystyle BC}$, ${\displaystyle G}$ on ${\displaystyle CD}$, and ${\displaystyle H}$ on ${\displaystyle DA}$, then for any point ${\displaystyle P}$ on the inscribed circle,^[30]$${\displaystyle 2(PH^{2}-PE^{2})=PD^{2}-PB^{2}.}$$ If ${\displaystyle d_{i}}$ is the distance from an arbitrary point in the plane to the ${\displaystyle i}$th vertex of a square and ${\displaystyle R}$ is the circumradius of the square, then^[31]$${\displaystyle {\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+3R^{4}=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+R^{2}\right)^{2}.}$$ If ${\displaystyle L}$ and ${\displaystyle d_{i}}$ are the distances from an arbitrary point in the plane to the centroid of the square and its four vertices respectively, then $${\displaystyle d_{1}^{2}+d_{3}^{2}=d_{2}^{2}+d_{4}^{2}=2(R^{2}+L^{2})}$$ and $${\displaystyle d_{1}^{2}d_{3}^{2}+d_{2}^{2}d_{4}^{2}=2(R^{4}+L^{4}),}$$ where ${\displaystyle R}$ is the circumradius of the square.^[32]

Applications

Square tiles

Pixelated Girl with a Pearl Earring

Squares are so well-established as the shape of tiles that the Latin word tessera, for a small tile as used in mosaics, comes from an ancient Greek word for the number four, referring to the four corners of a square tile.^[33] Graph paper, preprinted with a square tiling, is widely used for data visualization using Cartesian coordinates.^[34] The pixels of bitmap images, as recorded by image scanners and digital cameras or displayed on electronic visual displays, conventionally lie at the intersections of a square grid, and are often considered as small squares, arranged in a square tiling.^[35][36] Standard techniques for image compression and video compression, including the JPEG format, are based on the subdivision of images into larger square blocks of pixels.^[37] The quadtree data structure used in data compression and computational geometry is based on the recursive subdivision of squares into smaller squares.^[38]

Site of the Yongning Pagoda

Architectural structures from both ancient and modern cultures have featured a square floor plan, base, or footprint. Ancient examples include the Egyptian pyramids,^[39] Mesoamerican pyramids such as those at Teotihuacan,^[40] the Chogha Zanbil ziggurat in Iran,^[41] the four-fold design of Persian walled gardens, said to model the four rivers of Paradise, and later structures inspired by their design such as the Taj Mahal in India,^[42] the square bases of Buddhist stupas,^[43] and East Asian pagodas, buildings that symbolically face to the four points of the compass and reach to the heavens.^[44] Norman keeps such as the Tower of London often take the form of a low square tower.^[45] In modern architecture, a majority of skyscrapers feature a square plan for pragmatic rather than aesthetic or symbolic reasons.^[46]

A Tibetan mandala

Broadway Boogie Woogie, Piet Mondrian

The stylized nested squares of a Tibetan mandala, like the design of a stupa, function as a miniature model of the cosmos.^[47] Some formats for film photography use a square aspect ratio, notably Polaroid cameras, medium format cameras, and Instamatic cameras.^[48][49] Painters known for their frequent use of square frames and forms include Josef Albers,^[50] Kazimir Malevich^[51] and Piet Mondrian.^[52]

Baseball diamonds^[53] and boxing rings are square despite being named for other shapes.^[54] In the quadrille and square dance, four couples form the sides of a square.^[55] In Samuel Beckett's minimalist television play Quad, four actors walk along the sides and diagonals of a square.^[56]

16th-century Indian chessboard

Ostomachion

1615 horoscope

The square go board is said to represent the earth, with the 361 crossings of its lines representing days of the year.^[57] The chessboard inherited its square shape from a pachisi-like Indian race game and in turn passed it on to checkers.^[58] In two ancient games from Mesopotamia and Ancient Egypt, the Royal Game of Ur and Senet, the game board itself is not square, but rectangular, subdivided into a grid of squares.^[59] The ancient Greek Ostomachion puzzle (according to some interpretations) involves rearranging the pieces of a square cut into smaller polygons, as does the Chinese tangram.^[60] Another set of puzzle pieces, the polyominos, are formed from squares glued edge-to-edge.^[61] Medieval and Renaissance horoscopes were arranged in a square format, across Europe, the Middle East, and China.^[62] Other recreational uses of squares include the shape of origami paper,^[63] and a common style of quilting involving the use of square quilt blocks.^[64]

Square flag of the municipality of Vuadens, based on the Swiss flag

QR code for the mobile English Wikipedia

Square waffles

Squares are a common element of graphic design, used to give a sense of stability, symmetry, and order.^[65] In heraldry, a canton (a design element in the top left of a shield) is normally square, and a square flag is called a banner.^[66] The flag of Switzerland is square, as are the flags of the Swiss cantons.^[67] QR codes are square and feature prominent nested square alignment marks in three corners.^[68] Robertson screws have a square drive socket.^[69] Crackers and sliced cheese are often square,^[70] as are waffles.^[71][72] Square foods named for their square shapes include caramel squares, date squares, lemon squares,^[73] square sausage,^[74] and Carré de l'Est cheese.^[75]

Constructions

Coordinates and equations

${\displaystyle |x|+|y|=2}$ plotted on Cartesian coordinates.

A unit square is a square of side length one. Often it is represented in Cartesian coordinates as the square enclosing the points ${\displaystyle (x,y)}$ that have ${\displaystyle 0\leq x\leq 1}$ and ${\displaystyle 0\leq y\leq 1}$. Its vertices are the four points that have 0 or 1 in each of their coordinates.^[76]

An axis-parallel square with its center at the point ${\displaystyle (x_{c},y_{c})}$ and sides of length ${\displaystyle 2r}$ (where ${\displaystyle r}$ is the inradius, half the side length) has vertices at the four points ${\displaystyle (x_{c}\pm r,y_{c}\pm r)}$. Its interior consists of the points ${\displaystyle (x,y)}$ with ${\displaystyle \max(|x-x_{c}|,|y-y_{c}|)<r}$, and its boundary consists of the points with ${\displaystyle \max(|x-x_{c}|,|y-y_{c}|)=r}$.^[77]

A diagonal square with its center at the point ${\displaystyle (x_{c},y_{c})}$ and diagonal of length ${\displaystyle 2R}$ (where ${\displaystyle R}$ is the circumradius, half the diagonal) has vertices at the four points ${\displaystyle (x_{c}\pm R,y_{c})}$ and ${\displaystyle (x_{c},y_{c}\pm R)}$. Its interior consists of the points ${\displaystyle (x,y)}$ with ${\displaystyle |x-x_{c}|+|y-y_{c}|<R}$, and its boundary consists of the points with ${\displaystyle |x-x_{c}|+|y-y_{c}|=R}$.^[77] For instance the illustration shows a diagonal square centered at the origin ${\displaystyle (0,0)}$ with circumradius 2, given by the equation ${\displaystyle |x|+|y|=2}$.

A square formed by multiplying the complex number p by powers of i, and its translation obtained by adding another complex number c. The background grid shows the Gaussian integers.

In the plane of complex numbers, multiplication by the imaginary unit ${\displaystyle i}$ rotates the other term in the product by 90° around the origin (the number zero). Therefore, if any nonzero complex number ${\displaystyle p}$ is repeatedly multiplied by ${\displaystyle i}$, giving the four numbers ${\displaystyle p}$, ${\displaystyle ip}$, ${\displaystyle -p}$, and ${\displaystyle -ip}$, these numbers will form the vertices of a square centered at the origin.^[78] If one interprets the real part and imaginary part of these four complex numbers as Cartesian coordinates, with ${\displaystyle p=x+iy}$, then these four numbers have the coordinates ${\displaystyle (x,y)}$, ${\displaystyle (-y,x)}$, ${\displaystyle (-x,-y)}$, and ${\displaystyle (-y,-x)}$.^[79] This square can be translated to have any other complex number ${\displaystyle c}$ is center, using the fact that the translation from the origin to ${\displaystyle c}$ is represented in complex number arithmetic as addition with ${\displaystyle c}$.^[80] The Gaussian integers, complex numbers with integer real and imaginary parts, form a square lattice in the complex plane.^[80]

Compass and straightedge

The construction of a square with a given side, using a compass and straightedge, is given in Euclid's Elements I.46.^[81] The existence of this construction means that squares are constructible polygons. A regular ${\displaystyle n}$-gon is constructible exactly when the odd prime factors of ${\displaystyle n}$ are distinct Fermat primes,^[82] and in the case of a square ${\displaystyle n=4}$ has no odd prime factors so this condition is vacuously true.

Elements IV.6–7 also give constructions for a square inscribed in a circle and circumscribed about a circle, respectively.^[83]

• 
  Square with a given circumcircle
• 
  Square with a given side length, using Thales' theorem
• 
  Square with a given diagonal

Related topics

The cube and regular octahedron, next steps in sequences of regular polytopes starting with squares

The Sierpiński carpet, a square fractal with square holes

An invariant measure for the baker's map

The Schläfli symbol of a square is {4}.^[84] A truncated square is an octagon.^[85] The square belongs to a family of regular polytopes that includes the cube in three dimensions and the hypercubes in higher dimensions,^[86] and to another family that includes the regular octahedron in three dimensions and the cross-polytopes in higher dimensions.^[87] The cube and hypercubes can be given vertex coordinates that are all ${\displaystyle \pm 1}$, giving an axis-parallel square in two dimensions, while the octahedron and cross-polytopes have one coordinate ${\displaystyle \pm 1}$ and the rest zero, giving a diagonal square in two dimensions.^[88] As with squares, the symmetries of these shapes can be obtained by applying a signed permutation to their coordinates.^[23]

The Sierpiński carpet is a square fractal, with square holes.^[89] Space-filling curves including the Hilbert curve, Peano curve, and Sierpiński curve cover a square as the continuous image of a line segment.^[90] The Z-order curve is analogous but not continuous.^[91] Other mathematical functions associated with squares include Arnold's cat map and the baker's map, which generate chaotic dynamical systems on a square,^[92] and the lemniscate elliptic functions, complex functions periodic on a square grid.^[93]

Inscribed squares

The Calabi triangle and the three placements of its largest square.^[94] The placement on the long side of the triangle is inscribed; the other two are not.

Main articles: Inscribed square problem and Inscribed square in a triangle

A square is inscribed in a curve when all four vertices of the square lie on the curve. The unsolved inscribed square problem asks whether every simple closed curve has an inscribed square. It is true for every smooth curve,^[95] and for the boundary of any convex set. The only other regular polygon that can always be inscribed in every convex set is the equilateral triangle, as there exists a convex set on which no other regular polygon can be inscribed.^[96]

For an inscribed square in a triangle, at least one side of the square lies on a side of the triangle. Every acute triangle has three inscribed squares, one for each of its three sides. A right triangle has two inscribed squares, one touching its right angle and the other lying on its hypotenuse. An obtuse triangle has only one inscribed square, on its longest. A square inscribed in a triangle can cover at most half the triangle's area.^[97]

Area and quadrature

See also: Area, Quadrature (geometry), and Squaring the circle

The Pythagorean theorem: the two smaller squares on the sides of a right triangle have equal total area to the larger square on the hypotenuse.

A circle and square with the same area

Conventionally, since ancient times, most units of area have been defined in terms of various squares, typically a square with a standard unit of length as its side, for example a square meter or square inch.^[98] The area of an arbitrary rectangle can then be simply computed as the product of its length and its width, and more complicated shapes can be measured by conceptually breaking them up into unit squares or into arbitrary triangles.^[98]

In ancient Greek deductive geometry, the area of a planar shape was measured and compared by constructing a square with the same area by using only a finite number of steps with compass and straightedge, a process called quadrature or squaring. Euclid's Elements shows how to do this for rectangles, parallelograms, triangles, and then more generally for simple polygons by breaking them into triangular pieces.^[99] Some shapes with curved sides could also be squared, such as the lune of Hippocrates^[100] and the parabola.^[101]

This use of a square as the defining shape for area measurement also occurs in the Greek formulation of the Pythagorean theorem: squares constructed on the two sides of a right triangle have equal total area to a square constructed on the hypotenuse.^[102] Stated in this form, the theorem would be equally valid for other shapes on the sides of the triangle, such as equilateral triangles or semicircles,^[103] but the Greeks used squares. In modern mathematics, this formulation of the theorem using areas of squares has been replaced by an algebraic formulation involving squaring numbers: the lengths of the sides and hypotenuse of the right triangle obey the equation ${\displaystyle a^{2}+b^{2}=c^{2}}$.^[104]

Because of this focus on quadrature as a measure of area, the Greeks and later mathematicians sought unsuccessfully to square the circle, constructing a square with the same area as a given circle, again using finitely many steps with a compass and straightedge. In 1882, the task was proven to be impossible as a consequence of the Lindemann–Weierstrass theorem. This theorem proves that pi (π) is a transcendental number rather than an algebraic irrational number; that is, it is not the root of any polynomial with rational coefficients. A construction for squaring the circle could be translated into a polynomial formula for π, which does not exist.^[105]

Tiling and packing

Main articles: Square tiling, Square packing, Circle packing in a square, and Squaring the square

Square tiling

Pythagorean tiling

The square tiling, familiar from flooring and game boards, is one of three regular tilings of the plane. The other two use the equilateral triangle and the regular hexagon.^[106] The vertices of a square tiling form a square lattice.^[107] Squares of more than one size can also tile the plane,^[108][109] for instance in the Pythagorean tiling, named for its connection to proofs of the Pythagorean theorem.^[110]

The smallest known square that can contain 11 unit squares has side length approximately 3.877084.^[111]

Square packing problems seek the smallest square or circle into which a given number of unit squares can fit. A chessboard optimally packs a square number of unit squares into a larger square, but beyond a few special cases such as this, the optimal solutions to these problems remain unsolved;^{[111][112][113]} the same is true for circle packing in a square.^[114] Packing squares into other shapes can have high computational complexity: testing whether a given number of unit squares can fit into an orthogonally convex rectilinear polygon with half-integer vertex coordinates is NP-complete.^[115]

Squaring the square involves subdividing a given square into smaller squares, all having integer side lengths. A subdivision with distinct smaller squares is called a perfect squared square.^[116] Another variant of squaring the square called "Mrs. Perkins's quilt" allows repetitions, but uses as few smaller squares as possible in order to make the greatest common divisor of the side lengths be 1.^[117] The entire plane can be tiled by squares, with exactly one square of each integer side length.^[118]

Stereographic projection into 3d of a rotating Clifford torus

Regular skew apeirohedron with six squares per vertex

Numerical simulation of an inflated square pillow

In higher dimensions, other surfaces than the plane can be tiled by equal squares, meeting edge-to-edge. One of these surfaces is the Clifford torus, the four-dimensional Cartesian product of two congruent circles; it has the same intrinsic geometry as a single square with each pair of opposite edges glued together.^[119] Another square-tiled surface, a regular skew apeirohedron in three dimensions, has six squares meeting at each vertex.^[120] The paper bag problem seeks the maximum volume that can be enclosed by a surface tiled with two squares glued edge to edge; its exact answer is unknown.^[121] Gluing two squares in a different pattern, with the vertex of each square attached to the midpoint of an edge of the other square (or alternatively subdividing these two squares into eight squares glued edge-to-edge) produces a pincushion shape called a biscornu.^[122]

Counting

Main articles: Square pyramidal number and Dividing a square into similar rectangles

Two square-counting puzzles: There are 14 squares in a 3 × 3 grid of squares (top), but as a 4 × 4 grid of points it has six more off-axis squares (bottom) for a total of 20.

A common mathematical puzzle involves counting the squares of all sizes in a square grid of ${\displaystyle n\times n}$ squares. For instance, a square grid of nine squares has 14 squares: the nine squares that form the grid, four more ${\displaystyle 2\times 2}$ squares, and one ${\displaystyle 3\times 3}$ square. The answer to the puzzle is ${\displaystyle n(n+1)(2n+1)/6}$, a square pyramidal number.^[123] For ${\displaystyle n=1,2,3,\dots }$ these numbers are:^[124]

1, 5, 14, 30, 55, 91, 140, 204, 285, ...

A variant of the same puzzle asks for the number of squares formed by a grid of ${\displaystyle n\times n}$ points, allowing squares that are not axis-parallel. For instance, a grid of nine points has five axis-parallel squares as described above, but it also contains one more diagonal square for a total of six.^[125] In this case, the answer is given by the 4-dimensional pyramidal numbers ${\displaystyle n^{2}(n^{2}-1)/12}$. For ${\displaystyle n=1,2,3,\dots }$ these numbers are:^[126]

0, 1, 6, 20, 50, 105, 196, 336, 540, ...

Partitions of a square into three similar rectangles

Another counting problem involving squares asks for the number of different shapes of rectangle that can be used when dividing a square into similar rectangles.^[127] A square can be divided into two similar rectangles only in one way, by bisecting it, but when dividing a square into three similar rectangles there are three possible aspect ratios of the rectangles, 3:1, 3:2, and the square of the plastic ratio. The number of proportions that are possible when dividing into ${\displaystyle n}$ rectangles is known for small values of ${\displaystyle n}$, but not as a general formula. For ${\displaystyle n=1,2,3,\dots }$ these numbers are:^[128]

1, 1, 3, 11, 51, 245, 1372, ...

Other geometries

Concentric squares in the sphere (orthographic projection)

Concentric squares in the hyperbolic plane (conformal disk model)

An octant is a regular spherical triangle with right angles.

Regular hexagons with right angles can tile the hyperbolic plane with four hexagons meeting at each vertex.

In the familiar Euclidean geometry, space is flat, and every convex quadrilateral has internal angles summing to 360°, so a square (a regular quadrilateral) has four equal sides and four right angles (each 90°). By contrast, in spherical geometry and hyperbolic geometry, space is curved and the internal angles of a convex quadrilateral never sum to 360°, so quadrilaterals with four right angles do not exist. Both of these geometries have regular quadrilaterals, with four equal sides and four equal angles, often called squares,^[129] but some authors avoid that name because they lack right angles. These geometries also have regular polygons with right angles, but with numbers of sides different from four.^[130]

In spherical geometry, space has uniform positive curvature, and every convex quadrilateral (a polygon with four great-circle arc edges) has angles whose sum exceeds 360° by an amount called the angular excess, proportional to its surface area. Small spherical squares are approximately Euclidean, and larger squares' angles increase with area.^[129] One special case is the face of a spherical cube with four 120° angles, covering one sixth of the sphere's surface.^[131] Another is a hemisphere, the face of a spherical square dihedron, with four straight angles; the Peirce quincuncial projection for world maps conformally maps two such faces to Euclidean squares.^[132] An octant of a sphere is a regular spherical triangle, with three equal sides and three right angles; eight of them tile the sphere, with four meeting at each vertex, to form a spherical octahedron.^[133] A spherical lune is a regular digon, with two semicircular sides and two equal angles at antipodal vertices; a right-angled lune covers one quarter of the sphere, one face of a four-lune hosohedron.^[134]

In hyperbolic geometry, space has uniform negative curvature, and every convex quadrilateral has angles whose sum falls short of 360° by an amount called the angular defect, proportional to its surface area. Small hyperbolic squares are approximately Euclidean, and larger squares' angles decrease with increasing area. Special cases include the squares with angles of 360°/n for every value of n larger than 4, each of which can tile the hyperbolic plane.^[130] In the infinite limit, an ideal square has four sides of infinite length and four vertices at ideal points outside the hyperbolic plane, with 0° internal angles;^[135] an ideal square, like every ideal quadrilateral, has finite area proportional to its angular defect of 360°.^[136] It is also possible to make a regular hyperbolic polygon with right angles at every vertex and any number of sides greater than four; such polygons can uniformly tile the hyperbolic plane, dual to the tiling with n squares about each vertex.^[130]

Metric circles using Chebyshev, Euclidean, and taxicab distance functions

The Euclidean plane can be defined in terms of the real coordinate plane by adoption of the Euclidean distance function, according to which the distance between any two points ${\displaystyle (x_{1},y_{1})}$ and ${\displaystyle (x_{2},y_{2})}$ is ${\displaystyle \textstyle {\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}}$. Other metric geometries are formed when a different distance function is adopted instead. Shapes that would be Euclidean squares become the "circles" (set of points of equal distance from a center point). Squares tilted at 45° to the coordinate axes are the circles in taxicab geometry, based on the ${\displaystyle L_{1}}$ distance ${\displaystyle |x_{1}-x_{2}|+|y_{1}-y_{2}|}$. The points with taxicab distance ${\displaystyle d}$ from any given point form a diagonal square, centered at the given point, with diagonal length ${\displaystyle 2d}$. In the same way, axis-parallel squares are the circles for the ${\displaystyle L_{\infty }}$ or Chebyshev distance, ${\displaystyle \max(|x_{1}-x_{2}|,|y_{1}-y_{2}|)}$. In this metric, the points with distance ${\displaystyle d}$ from some point form an axis-parallel square, centered at the given point, with side length ${\displaystyle 2d}$.^{[137][138][139]}

See also

• Mathematics portal

• Finsler–Hadwiger theorem on a square derived from two squares sharing a vertex
• Midsquare quadrilateral, a polygon whose edge midpoints form a square
• Monsky's theorem, on subdividing a square into an odd number of equal-area triangles
• Square planar molecular geometry, chemical structure with atoms at the corners of a square
• Square trisection, a problem of cutting and reassembling one square into three squares
• Squircle, a shape intermediate between a square and a circle
• Tarski's circle-squaring problem, dividing a disk into sets that can be rearranged into a square
• Van Aubel's theorem and Thébault's theorem, on squares placed on the sides of a quadrilateral