Bitruncation
Operation in Euclidean geometry From Wikipedia, the free encyclopedia
In geometry, a bitruncation is an operation on regular polytopes. The original edges are lost completely and the original faces remain as smaller copies of themselves.


Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation t1,2{p,q,...} or 2t{p,q,...}.
In regular polyhedra and tilings
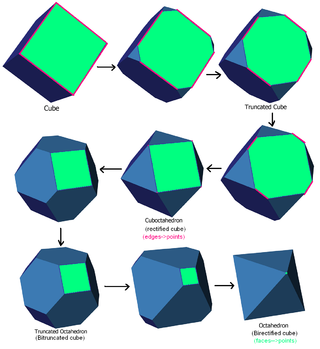
For regular polyhedra (i.e. regular 3-polytopes), a bitruncated form is the truncated dual. For example, a bitruncated cube is a truncated octahedron.
In regular 4-polytopes and honeycombs
Summarize
Perspective
For a regular 4-polytope, a bitruncated form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual.
A regular polytope (or honeycomb) {p, q, r} will have its {p, q} cells bitruncated into truncated {q, p} cells, and the vertices are replaced by truncated {q, r} cells.
Self-dual {p,q,p} 4-polytope/honeycombs
An interesting result of this operation is that self-dual 4-polytope {p,q,p} (and honeycombs) remain cell-transitive after bitruncation. There are 5 such forms corresponding to the five truncated regular polyhedra: t{q,p}. Two are honeycombs on the 3-sphere, one a honeycomb in Euclidean 3-space, and two are honeycombs in hyperbolic 3-space.
| Space | 4-polytope or honeycomb | Schläfli symbol Coxeter-Dynkin diagram |
Cell type | Cell image |
Vertex figure |
|---|---|---|---|---|---|
| Bitruncated 5-cell (10-cell) (Uniform 4-polytope) |
t1,2{3,3,3} |
truncated tetrahedron | 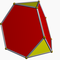 |
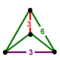 | |
| Bitruncated 24-cell (48-cell) (Uniform 4-polytope) |
t1,2{3,4,3} |
truncated cube |  |
 | |
| Bitruncated cubic honeycomb (Uniform Euclidean convex honeycomb) |
t1,2{4,3,4} |
truncated octahedron |  |
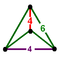 | |
| Bitruncated icosahedral honeycomb (Uniform hyperbolic convex honeycomb) |
t1,2{3,5,3} |
truncated dodecahedron |  |
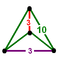 | |
| Bitruncated order-5 dodecahedral honeycomb (Uniform hyperbolic convex honeycomb) |
t1,2{5,3,5} |
truncated icosahedron |  |
 |
See also
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
External links
| Seed | Truncation | Rectification | Bitruncation | Dual | Expansion | Omnitruncation | Alternations | ||
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 | |||||
| t0{p,q} {p,q} |
t01{p,q} t{p,q} |
t1{p,q} r{p,q} |
t12{p,q} 2t{p,q} |
t2{p,q} 2r{p,q} |
t02{p,q} rr{p,q} |
t012{p,q} tr{p,q} |
ht0{p,q} h{q,p} |
ht12{p,q} s{q,p} |
ht012{p,q} sr{p,q} |
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
 ,
,  ...
...