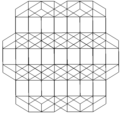
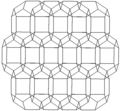
Bitruncated cubic honeycomb

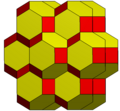
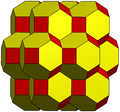
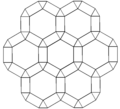
The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of truncated octahedra (or, equivalently, bitruncated cubes). It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.

Bitruncated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	2t{4,3,4} t1,2{4,3,4}
Coxeter-Dynkin diagram
Cell type	(4.6.6)
Face types	square {4} hexagon {6}
Edge figure	isosceles triangle {3}
Vertex figure	(tetragonal disphenoid)
Space group Fibrifold notation Coxeter notation	Im3m (229) 8o:2 [[4,3,4]]
Coxeter group	${\displaystyle {\tilde {C}}_{3}}$, [4,3,4]
Dual	Oblate tetrahedrille Disphenoid tetrahedral honeycomb Cell: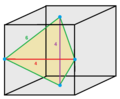
Properties	isogonal, isotoxal, isochoric

The bitruncated cubic honeycomb shown here in relation to a cubic honeycomb

John Horton Conway calls this honeycomb a truncated octahedrille in his Architectonic and catoptric tessellation list, with its dual called an oblate tetrahedrille, also called a disphenoid tetrahedral honeycomb. Although a regular tetrahedron can not tessellate space alone, this dual has identical disphenoid tetrahedron cells with isosceles triangle faces.

Geometry

It can be realized as the Voronoi tessellation of the body-centred cubic lattice. Lord Kelvin conjectured that a variant of the bitruncated cubic honeycomb (with curved faces and edges, but the same combinatorial structure) was the optimal soap bubble foam. However, a number of less symmetrical structures have later been found to be more efficient foams of soap bubbles, among which the Weaire–Phelan structure appears to be the best.

The honeycomb represents the permutohedron tessellation for 3-space. The coordinates of the vertices for one octahedron represent a hyperplane of integers in 4-space, specifically permutations of (1,2,3,4). The tessellation is formed by translated copies within the hyperplane.

The tessellation is the highest tessellation of parallelohedrons in 3-space.

Projections

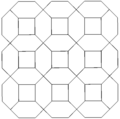
The bitruncated cubic honeycomb can be orthogonally projected into the euclidean plane with various symmetry arrangements. The highest (hexagonal) symmetry form projects into a nonuniform rhombitrihexagonal tiling. A square symmetry projection forms two overlapping truncated square tiling, which combine together as a chamfered square tiling.

Orthogonal projections

Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame

Symmetry

The vertex figure for this honeycomb is a disphenoid tetrahedron, and it is also the Goursat tetrahedron (fundamental domain) for the ${\displaystyle {\tilde {A}}_{3}}$ Coxeter group. This honeycomb has four uniform constructions, with the truncated octahedral cells having different Coxeter groups and Wythoff constructions. These uniform symmetries can be represented by coloring differently the cells in each construction.

Five uniform colorings by cell

Space group	Im3m (229)	Pm3m (221)	Fm3m (225)	F43m (216)	Fd3m (227)
Fibrifold	8o:2	4−:2	2−:2	1o:2	2+:2
Coxeter group	${\displaystyle {\tilde {C}}_{3}}$×2 [[4,3,4]] =[4[3[4]]] =	${\displaystyle {\tilde {C}}_{3}}$ [4,3,4] =[2[3[4]]] =	${\displaystyle {\tilde {B}}_{3}}$ [4,31,1] =<[3[4]]> =	${\displaystyle {\tilde {A}}_{3}}$ [3[4]]	${\displaystyle {\tilde {A}}_{3}}$×2 [[3[4]]] =[[3[4]]]
Coxeter diagram
truncated octahedra	1	1:1 :	2:1:1 ::	1:1:1:1 :::	1:1 :
Vertex figure
Vertex figure symmetry	[2+,4] (order 8)	[2] (order 4)	[ ] (order 2)	[ ]+ (order 1)	[2]+ (order 2)
Image Colored by cell

Related polyhedra and honeycombs

The regular skew apeirohedron {6,4|4} contains the hexagons of this honeycomb.

The [4,3,4], , Coxeter group generates 15 permutations of uniform tessellations, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.

C3 honeycombs
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Pm3m (221)	4−:2	[4,3,4]		×1	1, 2, 3, 4, 5, 6
Fm3m (225)	2−:2	[1+,4,3,4] ↔ [4,31,1]	↔	Half	7, 11, 12, 13
I43m (217)	4o:2	[[(4,3,4,2+)]]		Half × 2	(7),
Fd3m (227)	2+:2	[[1+,4,3,4,1+]] ↔ [[3[4]]]	↔	Quarter × 2	10,
Im3m (229)	8o:2	[[4,3,4]]		×2	(1), 8, 9

The [4,3^1,1], , Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.

B3 honeycombs
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Fm3m (225)	2−:2	[4,31,1] ↔ [4,3,4,1+]	↔	×1	1, 2, 3, 4
Fm3m (225)	2−:2	<[1+,4,31,1]> ↔ <[3[4]]>	↔	×2	(1), (3)
Pm3m (221)	4−:2	<[4,31,1]>		×2	5, 6, 7, (6), 9, 10, 11

This honeycomb is one of five distinct uniform honeycombs^[1] constructed by the ${\displaystyle {\tilde {A}}_{3}}$ Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:

A3 honeycombs
Space group	Fibrifold	Square symmetry	Extended symmetry	Extended diagram	Extended group	Honeycomb diagrams
F43m (216)	1o:2	a1	[3[4]]		${\displaystyle {\tilde {A}}_{3}}$	(None)
Fm3m (225)	2−:2	d2	<[3[4]]> ↔ [4,31,1]	↔	${\displaystyle {\tilde {A}}_{3}}$×21 ↔ ${\displaystyle {\tilde {B}}_{3}}$	1, 2
Fd3m (227)	2+:2	g2	[[3[4]]] or [2+[3[4]]]	↔	${\displaystyle {\tilde {A}}_{3}}$×22	3
Pm3m (221)	4−:2	d4	<2[3[4]]> ↔ [4,3,4]	↔	${\displaystyle {\tilde {A}}_{3}}$×41 ↔ ${\displaystyle {\tilde {C}}_{3}}$	4
I3 (204)	8−o	r8	[4[3[4]]]+ ↔ [[4,3+,4]]	↔	½${\displaystyle {\tilde {A}}_{3}}$×8 ↔ ½${\displaystyle {\tilde {C}}_{3}}$×2	(*)
Im3m (229)	8o:2		[4[3[4]]] ↔ [[4,3,4]]		${\displaystyle {\tilde {A}}_{3}}$×8 ↔ ${\displaystyle {\tilde {C}}_{3}}$×2	5

Alternated form

Alternated bitruncated cubic honeycomb
Type	Convex honeycomb
Schläfli symbol	2s{4,3,4} 2s{4,31,1} sr{3[4]}
Coxeter diagrams	= = =
Cells	tetrahedron icosahedron
Vertex figure
Coxeter group	[[4,3+,4]], ${\displaystyle {\tilde {C}}_{3}}$
Dual	Ten-of-diamonds honeycomb Cell:
Properties	vertex-transitive

This honeycomb can be alternated, creating pyritohedral icosahedra from the truncated octahedra with disphenoid tetrahedral cells created in the gaps. There are three constructions from three related Coxeter-Dynkin diagrams: , , and . These have symmetry [4,3⁺,4], [4,(3^1,1)⁺] and [3^[4]]⁺ respectively. The first and last symmetry can be doubled as [[4,3⁺,4]] and [[3^[4]]]⁺.

The dual honeycomb is made of cells called ten-of-diamonds decahedra.

Five uniform colorings

Space group	I3 (204)	Pm3 (200)	Fm3 (202)	Fd3 (203)	F23 (196)
Fibrifold	8−o	4−	2−	2o+	1o
Coxeter group	[[4,3+,4]]	[4,3+,4]	[4,(31,1)+]	[[3[4]]]+	[3[4]]+
Coxeter diagram
Order	double	full	half	quarter double	quarter
Image colored by cells

This honeycomb is represented in the boron atoms of the α-rhombohedral crystal. The centers of the icosahedra are located at the fcc positions of the lattice.^[2]

Related polytopes

Nonuniform variants with [4,3,4] symmetry and two types of truncated octahedra can be doubled by placing the two types of truncated octahedra to produce a nonuniform honeycomb with truncated octahedra and hexagonal prisms (as ditrigonal trapezoprisms). Its vertex figure is a C_2v-symmetric triangular bipyramid.

This honeycomb can then be alternated to produce another nonuniform honeycomb with pyritohedral icosahedra, octahedra (as triangular antiprisms), and tetrahedra (as sphenoids). Its vertex figure has C_2v symmetry and consists of 2 pentagons, 4 rectangles, 4 isosceles triangles (divided into two sets of 2), and 4 scalene triangles.

See also

• Architectonic and catoptric tessellation
• Cubic honeycomb
• Brillouin zone

Notes

1. , A000029 6-1 cases, skipping one with zero marks
2. Williams, 1979, p 199, Figure 5-38.

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
• George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
• Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
• A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
• Klitzing, Richard. "3D Euclidean Honeycombs o4x3x4o - batch - O16".
• Uniform Honeycombs in 3-Space: 05-Batch
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.

External links

• Weisstein, Eric W. "Space-filling polyhedron". MathWorld.