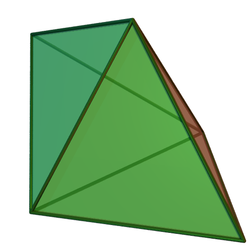
Triangular bipyramid

A triangular bipyramid is a hexahedron with six triangular faces constructed by attaching two tetrahedra face-to-face. The same shape is also known as a triangular dipyramid^[1][2] or trigonal bipyramid.^[3] If these tetrahedra are regular, all faces of a triangular bipyramid are equilateral. It is an example of a deltahedron, composite polyhedron, and Johnson solid.

Triangular bipyramid
Type	Bipyramid Deltahedra Johnson J11 – J12 – J13
Faces	6 triangles
Edges	9
Vertices	5
Vertex configuration	${\displaystyle 3\times (3^{2})+6\times (3^{2})}$
Symmetry group	${\displaystyle D_{3\mathrm {h} }}$
Dihedral angle (degrees)	As a Johnson solid: triangle-to-triangle: 70.5° triangle-to-triangle if tetrahedrons being attached: 141.1°
Dual polyhedron	triangular prism
Properties	convex, composite, face-transitive

Many polyhedra are related to the triangular bipyramid, such as similar shapes derived from different approaches and the triangular prism as its dual polyhedron. Applications of a triangular bipyramid include trigonal bipyramidal molecular geometry which describes its atom cluster, a solution of the Thomson problem, and the representation of color order systems by the eighteenth century.

Special cases

As a right bipyramid

Like other bipyramids, a triangular bipyramid can be constructed by attaching two tetrahedra face-to-face.^[2] These tetrahedra cover their triangular base, and the resulting polyhedron has six triangles, five vertices, and nine edges.^[3] A triangular bipyramid is said to be right if the tetrahedra are symmetrically regular and both of their apices are on a line passing through the center of the base; otherwise, it is oblique.^[4][5]

Graph of a triangular bipyramid

According to Steinitz's theorem, a graph can be represented as the skeleton of a polyhedron if it is a planar (the edges of the graph do not cross, but intersect at the point) and three-connected graph (one of any two vertices leaves a connected subgraph when removed). A triangular bipyramid is represented by a graph with nine edges, constructed by adding one vertex to the vertices of a wheel graph representing tetrahedra.^[6][7]

Like other right bipyramids, a triangular bipyramid has three-dimensional point-group symmetry, the dihedral group ${\displaystyle D_{3\mathrm {h} }}$ of order twelve: the appearance of a triangular bipyramid is unchanged as it rotated by one-, two-thirds, and full angle around the axis of symmetry (a line passing through two vertices and the base's center vertically), and it has mirror symmetry with any bisector of the base; it is also symmetrical by reflection across a horizontal plane.^[8] A triangular bipyramid is face-transitive, or isohedral.^[9]

As a Johnson solid

Triangular bipyramid with regular faces alongside its net

3D model of a triangular bipyramid as a Johnson solid

If the tetrahedra are regular, all edges of a triangular bipyramid are equal in length and form equilateral triangular faces. A polyhedron with only equilateral triangles as faces is called a deltahedron. There are eight convex deltahedra, one of which is a triangular bipyramid with regular polygonal faces.^[1] A convex polyhedron in which all of its faces are regular polygons is the Johnson solid, and every convex deltahedron is a Johnson solid. A triangular bipyramid with regular faces is numbered as the twelfth Johnson solid ${\displaystyle J_{12}}$.^[10] It is an example of a composite polyhedron because it is constructed by attaching two regular tetrahedra.^[11][12]

A triangular bipyramid's surface area ${\displaystyle A}$ is six times that of each triangle. Its volume ${\displaystyle V}$ can be calculated by slicing it into two tetrahedra and adding their volume. In the case of edge length ${\displaystyle a}$, this is:^[12] $${\displaystyle {\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}a^{2}&\approx 2.598a^{2},\\V&={\frac {\sqrt {2}}{6}}a^{3}&\approx 0.238a^{3}.\end{aligned}}}$$

The dihedral angle of a triangular bipyramid can be obtained by adding the dihedral angle of two regular tetrahedra. The dihedral angle of a triangular bipyramid between adjacent triangular faces is that of the regular tetrahedron: 70.5 degrees. In an edge where two tetrahedra are attached, the dihedral angle of adjacent triangles is twice that: 141.1 degrees.^[13]

Related polyhedra

The Goldner–Harary graph represents a triangular bipyramid, augmented by tetrahedra.

Some types of triangular bipyramids may be derived in different ways. The Kleetope of a polyhedron is a construction involving the attachment of pyramids. A triangular bipyramid's Kleetope can be constructed from a triangular bipyramid by attaching tetrahedra to each of its faces, replacing them with three other triangles; the skeleton of the resulting polyhedron represents the Goldner–Harary graph.^[14][15] Another type of triangular bipyramid results from cutting off its vertices, a process known as truncation.^[16]

Bipyramids are the dual polyhedron of prisms. This means the bipyramids' vertices correspond to the faces of a prism, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other; doubling it results in the original polyhedron. A triangular bipyramid is the dual polyhedron of a triangular prism, and vice versa.^[17][3] A triangular prism has five faces, nine edges, and six vertices, with the same symmetry as a triangular bipyramid.^[3]

Applications

The known solution of the Thomson problem, with one a triangular bipyramid

The Thomson problem concerns the minimum energy configuration of charged particles on a sphere. A triangular bipyramid is a known solution in the case of five electrons, placing vertices of a triangular bipyramid within a sphere.^[18] This solution is aided by a mathematically rigorous computer.^[19]

A chemical compound's trigonal bipyramidal molecular geometry may be described as the atom cluster of a triangular bipyramid. This molecule has a main-group element without an active lone pair, described by a model which predicts the geometry of molecules known as VSEPR theory.^[20] Examples of this structure include phosphorus pentafluoride and phosphorus pentachloride in the gaseous phase.^[21]

In color theory, the triangular bipyramid was used to represent the three-dimensional color-order system in primary colors. German astronomer Tobias Mayer wrote in 1758 that each of its vertices represents a color: white and black are the top and bottom axial vertices, respectively, and the rest of the vertices are red, blue, and yellow.^[22][23]

References

1. Trigg, Charles W. (1978). "An infinite class of deltahedra". Mathematics Magazine. 51 (1): 55–57. doi:10.1080/0025570X.1978.11976675. JSTOR 2689647. MR 1572246.
2. Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. p. 84. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
3. King, Robert B. (1994). "Polyhedral Dynamics". In Bonchev, Danail D.; Mekenyan, O.G. (eds.). Graph Theoretical Approaches to Chemical Reactivity. Springer. doi:10.1007/978-94-011-1202-4. ISBN 978-94-011-1202-4.
4. Niu, Wenxin; Xu, Guobao (2011). "Crystallographic control of noble metal nanocrystals". Nano Today. 6 (3): 265–285. doi:10.1016/j.nantod.2011.04.006.
5. Alexandrov, Victor (2017). "How many times can the volume of a convex polyhedron be increased by isometric deformations?". Beiträge zur Algebra und Geometrie. 58 (3): 549–554. arXiv:1607.06604. doi:10.1007/s13366-017-0336-8.
6. Tutte, W. T. (2001). Graph Theory. Cambridge University Press. p. 113. ISBN 978-0-521-79489-3.
7. Sajjad, Wassid; Sardar, Muhammad S.; Pan, Xiang-Feng (2024). "Computation of resistance distance and Kirchhoff index of chain of triangular bipyramid hexahedron". Applied Mathematics and Computation. 461: 1–12. doi:10.1016/j.amc.2023.128313. S2CID 261797042.
8. Alexander, Daniel C.; Koeberlin, Geralyn M. (2014). Elementary Geometry for College Students (6th ed.). Cengage Learning. p. 403. ISBN 978-1-285-19569-8.
9. McLean, K. Robin (1990). "Dungeons, dragons, and dice". The Mathematical Gazette. 74 (469): 243–256. doi:10.2307/3619822. JSTOR 3619822. S2CID 195047512.
10. Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
11. Timofeenko, A. V. (2009). "Convex Polyhedra with Parquet Faces" (PDF). Docklady Mathematics. 80 (2): 720–723. doi:10.1134/S1064562409050238.
12. Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
13. Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
14. Grünbaum, Branko (1967). Convex Polytopes. Wiley Interscience. p. 357.. Same page, 2nd ed., Graduate Texts in Mathematics 221, Springer-Verlag, 2003, ISBN 978-0-387-40409-7.
15. Ewald, Günter (1973). "Hamiltonian circuits in simplicial complexes". Geometriae Dedicata. 2 (1): 115–125. doi:10.1007/BF00149287. S2CID 122755203.
16. Haji-Akbari, Amir; Chen, Elizabeth R.; Engel, Michael; Glotzer, Sharon C. (2013). "Packing and self-assembly of truncated triangular bipyramids". Phys. Rev. E. 88 (1): 012127. arXiv:1304.3147. Bibcode:2013PhRvE..88a2127H. doi:10.1103/physreve.88.012127. PMID 23944434. S2CID 8184675..
17. Sibley, Thomas Q. (2015). Thinking Geometrically: A Survey of Geometries. Mathematical Association of American. p. 53. ISBN 978-1-939512-08-6.
18. Sloane, N. J. A.; Hardin, R. H.; Duff, T. D. S.; Conway, J. H. (1995), "Minimal-energy clusters of hard spheres", Discrete & Computational Geometry, 14 (3): 237–259, doi:10.1007/BF02570704, MR 1344734, S2CID 26955765
19. Schwartz, Richard Evan (2013). "The Five-Electron Case of Thomson's Problem". Experimental Mathematics. 22 (2): 157–186. doi:10.1080/10586458.2013.766570. S2CID 38679186.
20. Petrucci, R. H.; Harwood, W. S.; Herring, F. G. (2002). General Chemistry: Principles and Modern Applications (8th ed.). Prentice-Hall. pp. 413–414. ISBN 978-0-13-014329-7. See table 11.1.
21. Housecroft, C. E.; Sharpe, A. G. (2004). Inorganic Chemistry (2nd ed.). Prentice Hall. p. 407. ISBN 978-0-13-039913-7.
22. Kuehni, Rolf G. (2003). Color Space and Its Divisions: Color Order from Antiquity to the Present. John & Sons Wiley. p. 53. ISBN 978-0-471-46146-3.
23. Kuehni, Rolf G. (2013). Color: An Introduction to Practice and Principles. John & Sons Wiley. p. 198. ISBN 978-1-118-17384-8.